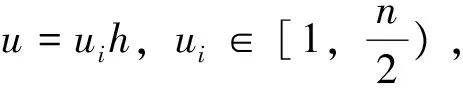C2⊕C2n上不可分原子的结构*
官欢欢,袁平之
(1. 贵州财经大学数学与统计学院,贵州 贵阳 550025;2. 华南师范大学数学科学学院,广东 广州 510631)
本文的符号参看文献[1]。
设G是有限阿贝尔群,由有限阿贝尔群结构定理知,存在n1,n2,…,nr∈,使得G≅Cn1⊕Cn2⊕…⊕Cnr,其中r=n1=1或者1 设F(G)是以群G为基的自由乘法阿贝尔幺半群。F(G)中的元素S称为群G上的序列,记为 supp(S)={g∈G|νg(S)>0}⊂G 因此序列S是由群G中元素组成的多重集。F(G)中的单位元素1称为空序列,记为φ,其长度为0。 若有νg(S)>0,称S包含元素g,记为g|S。 序列T∈F(G)称为序列S的子序列,如果对所有的g∈G,νg(T)≤νg(S),记为T|S。若1≤|T|<|S|,称T为S的真子序列。 如果T|S,则记ST-1为序列S去掉序列T中的元素之后所得的序列。 对任意的k∈{1,2,…,l},记 i1 如果0∉∑(S),称S为零和自由序列。 若S是群G上的零和序列,且其任意真子序列都是零和自由序列,则称S是最小零和序列。 若S是群G上的零和序列,并且1≤|S|≤exp(G),则称S为短零和序列。 群G的所有零和序列的集合记为B(G),所有最小零和序列的集合记为A(G)。 用D(G)记Davenport常数,即满足下列条件的最小的正整数d,使得群G中每个长度不小于d的序列都含有一个非空的零和子序列。 设G和G′都是有限阿贝尔群,S=g1·…·gl∈F(G),给定群同态φ:G→G′,将φ扩展到其生成的自由幺半群上的同态,定义φ(S)=φ(g1)·…·φ(gl),则φ为F(G)上的同态。 为了更好的给出本文的结论,首先给出下面两个定义。 定义 1[2]设S是群G上一个序列,称S是可分的原子(a splittable atom),如果S=(g1+g2)T,其中g1,g2∈G,T∈F(G)满足S∈A(G)且g1g2T∈A(G)。反之则称为不可分的(unsplittable)。 定义2[2]一个序列S∈F(G)称为光滑的(smooth),如果S=(n1g)·(n2g)·…·(nlg),其中 |S|∈,g∈G,1=n1≤n2≤…≤nl, n=n1+…+nl 且∑(S)={g,…,ng}(此时更确切地称S是g-光滑的)。 设S是群G上一个不可分原子。2009年,Savchev与Chen给出了阶为n的循环群上的长度超过其Davenport常数一半的不可分原子的结构,参看文献[2-6]。 本文给出了秩为2的有限阿贝尔群C2⊕C2n上不可分原子S的的具体结构。下面是本文的结论。 定理2 设S是群G=C2⊕C2n上长度为n+k,k≥4的不可分原子。则存在群G的阶为n的循环子群H= 引理3[7]设n≥2是正整数。每一个长度|S|≥3n-2的序列S∈F(Cn⊕Cn)包含一个短零和序列。 故可将S分拆为S=S1…SNS′,其中σ(Si)∈H,|Si|≤2,1≤i≤N,S′∩H=∅,h(S′)=1且|S′|≤3。设 A={S=S1…SNS′|σ(Si)∈H,|Si|≤2,1≤i≤N, 且S′∩H=∅,h(S′)=1,|S′|≤3} 设S∈A(G)是长度为n+k,k≥4的不可分原子。则由前面的讨论知存在h∈G使得ord(h)=n且G/H≅C2⊕C2,其中H= G=H∪(b+H)∪(c+H)∪(d+H),2b,2c,2d∈H且b+c+d∈H 因此可设S=ABCD,其中A∈F(H),B∈F(b+H),C∈F(c+H),D∈F(d+H)。由S∈A(G)知,|B|,|C|,|D|有相同的奇偶性。 ① 若|B|是偶数,则|C|,|D|均是偶数。对任意b1b2|B均有b1+b2∈H。同理C,D亦然。分别将B,C,D中的元素进行两两组合相加,则得到相应的序列的集合B,E,D。对任意AB∈B,AC∈E,AD∈D,可得序列T=AABACAD∈A(H)。故B,E,D⊂F(H),并且有 |T|=|A|+|AB|+|AC|+|AD|= 若|B|是奇数,则|C|,|D|均是奇数。对任意的bi∈B,cj∈C,dk∈D,分别将B{bi},C{cj},D{dk}中的元素进行两两组合相加,则得到相应的序列的集合Bi,Ej,Dk。对任意AB∈Bi,AC∈Ej,AD∈Dk,由上面的论述知,可得序列 T=AABACAD(bi+cj+dk)∈A(H), 且 |T|=|A|+|AB|+|AC|+|AD|+1= 为了更好的证明,首先给出一个断言。 断言1 如果下列的条件有一个成立,则S是可分的。 (i)g|A,g≠h; (ii)存在g|B,使得对任意的g′|Bg-1,g′+g≠h,且对任意的c|C,d|D,g′+c+d≠h。同理由对称性,条件对C,D也成立。 断言的证明:(i) 若存在g|A满足g=sh,s≥2,则g=(s-1)h+h。下面证明序列S′=Sg-1·(s-1)h·h是最小零和序列。欲证S′∈A(G),只需证明对任意U|S′h-1,U是零和自由的。 首先考虑(s-1)h|U。设U=A′·B′·C′·D′·(s-1)h,其中A′|A,B′|B,C′|C,D′|D是S的子序列。因为A′|A,B′|B,C′|C,D′|D,若σ(S′)=0,则|B′|,|C′|,|D′|的奇偶性相同。 最后考虑U不包含元素(s-1)h,显然U是零和自由的。 (ii)若存在g|B使得对任意的g′|Bg-1,g′+g≠h,且对任意的c|C,d|D,g′+c+d≠h,只需证明序列S′=Sg-1·(g-h)·h∈A(G)。显然σ(S′)=0。只需证明对任意的U|S′h-1=Sg-1·(g-h)是零和自由的。若U不包含元素(g-h),则U|S,|U|<|S|。 由S∈A(G)知,U是零和自由的。 若(g-h)|U,设U=A′·B′·C′·D′·(g-h)。 若σ(U)=0,则|B′|+1,|C′|+1,|D′|+1有相同的奇偶性。类似于(i)的讨论可得矛盾。因此U是零和自由的,故S′∈A(G)。断言得证。 ②A=ht,t≥0。 由断言1,显然可以得到。 ③ |supp(B)|≤2。同理|supp(C)|≤2,|supp(D)|≤2。 bi+bj+bk+bl=(bi+bj)+(bk+bl)=2h= (bk+bi)+(bj+bl)=(s+r)h 矛盾!因此|supp(B)|≤2。 ④ 若g1g2|B且g1≠g2,则g1+g2=h。同理对C,D结论亦成立。 由断言1可直接得到。 ⑤ 存在B,C,D中的一个满足其supp等于1。 由断言1以及④,结论显然成立。在下面的证明中,不妨设 |supp(B)|=1,B=bu,u≥2,2b=h ⑥A=∅,即A是空序列。 由⑤知,不妨设B=bu,u≥2,2b=h。若A≠∅,则h=2b。 从而Sh-1bu+2∈A(G)。故A=∅。 下面给出另外一个断言。 断言2 当C≠∅,D≠∅时,若存在c|C,对任意的d|D,均有c+d≠b,则S是可分的。 断言2的证明:若存在c|C,对任意的d|D,均有c+d≠b,考虑序列S′=S·c-1·(c-b)·b。下面证明S′∈A(G)。只需证明S·c-1·(c-b)是零和自由的。 对任意的U|S·c-1·(c-b),若U|S,则由S∈A(G)知,U是零和自由的。下设(c-b)|U。设U=B′C′D′(c-b),其中B′|B,C′|C,D′|D。若σ(U)=0,则|B′|,|C′|,|D′|+1有相同的奇偶性。应用①,显然与σ(U)≠0矛盾。因此S是可分的。断言得证。 ⑦ 当C≠∅,D≠∅时,C=cv,D=dw且min{v,w}=1。不妨设S=bucvd。 由③知|supp(C)|≤2,|supp(D)|≤2。 若|supp(C)|=2,设c1c2|C,c1≠c2。因为D≠∅,由断言2知, 存在dd′|D,使得c1+d=c2+d′=b。由2b=h知,c1+d+b=c2+d′+b=h。因为c1≠c2,故c2+d+b≠h,c1+d′+b≠h,矛盾。因此|supp(C)|=1。同理可证|supp(D)|=1。 若v≥2,w≥2,由断言1知2c=h,2d=h,故2c+2d=2h。由断言2知c+d=b。又由2b=h可得b+c+d=h,即2(c+d)=h,矛盾。因为C≠∅,D≠∅,所以min{v,w}=1。 ⑧D≠∅。 若D=∅,由S∈A(G)知,|B|,|D|均是偶数。由断言1知或者C=∅,或者C=cv,v≥2,2c=h,2|v。若C≠∅,则2c=2b=h,即2(c-d)=0。考虑序列S·c-1·(c-b)·b。显然S·c-1·(c-b)·b∈A(G),与S不可分矛盾,因此C=∅。此时S=b2n,ord(b)=2n,2b=h。但是存在c,d∈G,使得b=c+d,从而序列S′=b2n-1·c·d∈A(G),与S不可分矛盾。因此D≠∅。 综上可得S=bucvdw,其中min{v,w}=1,且2b=h,b=c+d,ord(b)=2n。 参考文献: [1] GEROLDINGER A, HALTER-KOCH F. Non-unique factorizations [M]. Boca Raton: Chapman&Hall/CRC, 2006. [2] GEROLDINGER A, RUZSA I. Combinatorial number theory and additive group theory [J]. Adv Courses Math CRM Barcelona, Birkhäuser, 2009:1-86. [3] SAVCHEV S, CHEN F. Long zero-free sequences in finite cyclic groups [J]. Discrete Mathematics, 2007, 307: 2671-2679. [4] SAVCHEV S, CHEN F. Long zero-free sequences in finite cyclic groups [J]. Discrete Mathematics, 2007, 308: 1-8. [5] YUAN P Z. On the index of minimal zero-sum sequences over finite cyclic groups [J]. J Combin Theory Ser A, 2007, 114: 1545-1551. [6] ZHUANG J J, YUAN P Z. Minimal zero-sum sequences in finite cyclic groups [J]. Taiwanese J Math, 2009, 13(3): 1007-1015. [7] GAO W D, GEROLDINGER A. On long minimal zero sequences in finite Abelian groups [J].Periodica Math Hungarica, 1999, 38: 179-211.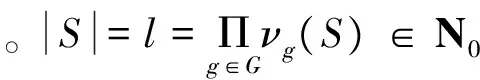

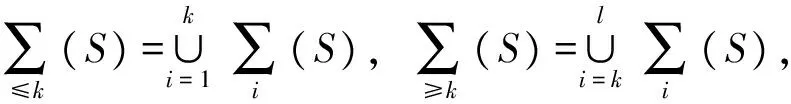


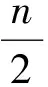
1 准备知识
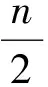
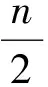


2 定理证明