两类图族的Merrifield－Simmons指标的最大值*

任胜章，郑国彪

(1.天水师范学院数学与统计学院，甘肃天水 741001;2.青海民族大学数学系，青海西宁 810007)

设图G=(V，E)是简单的连通图，并且V(G)是它的顶点集和E(G)是它的边集。对一个图G的任意两个顶点u和v，如果它们不相邻，则称它们是相互独立的。一个顶点集V(G)的子集I，如果它的任意两个顶点都相互独立，则称它是图G的一个独立集。用i(G)表示图G的独立集的个数，在化学中i(G)也被称为Merrifield－Simmons指标，此指标与化学分子的许多物理、化学性质密切相关，如分子的熔点、沸点等;对该指标的研究成果很多，参见文献 ［1－8］。

设Ck、Pk和Wk分别表示顶点数分别为k，k，k+1的圈，路和轮。则用Q(Ck;Cs1，Cs2，…，Csk)表示图族圈粘接圈是由圈Ck的每个顶点vi(i=1，2，…，k)分别点粘接圈Csi(i=1，2，…，k)而得到的图;用Q(Pk;Cs1，Cs2，…，Csk)表示图族路粘接圈是由路Pk的每个顶点vi(i=1，2，…，k)分别点粘接圈Csi(i=1，2，…，k)而得到的图;用Q(Wk;Cs1，Cs2，…，Csk)表示图族轮粘接圈是由轮Wk的每个顶点vi(i=1，2，…，k)(除中心顶点外)分别点粘接圈Csi(i=1，2，…，k)而得到的图。本文通过对图族Q(Ck;Cs1，Cs2，…，Csk)，Q(Wk;Cs1，Cs2，…，Csk)的Merrifield－Simmons指标进行研究，刻画出了这两类图族的Merrifield－Simmons指标在顶点数一定时，取得最大值的图分别是Q(Ck;C4，C4，…，C4，Cs1+s2+…+sk－4(k－1))，Q(Wk;C4，C4，…，C4，Cs1+s2+…+sk－4(k－1))。

在本文中没有给出的专业术语、记号可参见文献［9］。

1 预备引理

引理1［9］设图G1和G2是图G的两个分支，则i(G)=i(G1)i(G2)。

引理2［9］设图G是简单图且任意的v∈V(G)，则有i(G)=i(G－v)+i(G－NG［v］)，其中NG［v］是v的闭邻集。

引理 4［3］设图Q(Pk;Cs1，Cs2，…，Csk)是图族路粘接圈，在顶点数取定值时，则有i(Q(Pk;Cs1，Cs2，…，Csk))≤i(Q(Pk;C4，C4，…，C4，Cs1+s2+…+sk－4(k－1)))，等式成立当且仅当，Q(Pk;Cs1，Cs2，…，Csk)≅Q(Pk;C4，C4，…，C4，Cs1+s2+…+sk－4(k－1))。

2 主要结论

定理1 假设s1，s2，…，sk都是正整数且满足2≤s1≤s2≤…≤sk，在顶点数取定值时，则有:i(Ps1∪Ps2∪…∪Psk)≥i(P3∪P3∪…∪P3∪Ps1+s2+…+sk－3(k－1))，等式成立当且仅当，Ps1∪Ps2∪… ∪PskP3∪P3∪ … ∪P3∪Ps1+s2+…+sk－3(k－1)。

证明 (归纳法)假设n是路并图Ps1∪Ps2∪…∪Psk的分支数，那么当n=2时，由引理1，引理2和引理3得到

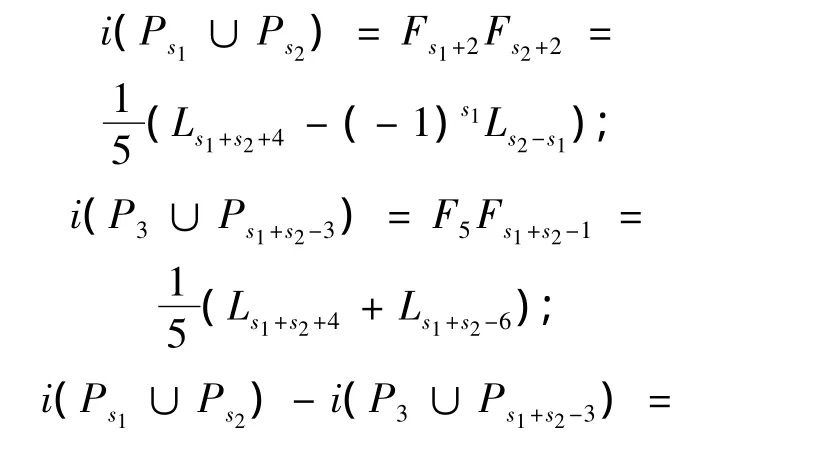
等号成立当且仅当，s1=3。所以当n=2时，结论成立。假设当n=k时，结论成立。即i(Ps1∪Ps2∪…∪Psk)≤i(P3∪P3∪…∪P3∪Ps1+s2+…+sk－3(k－1))，那么当n=k+1 时，由归纳假设，我们得到

所以

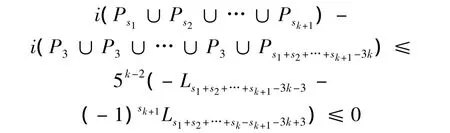
等式成立当且仅当，sk+1=3。

由上面两个证明过程可知，当n取遍所有大于2的自然数时，结论都成立。

定理2 假设s1，s2，…，sn都是正整数且满足si≥3(i=1，2，…，n)，在顶点数取定值时，则有

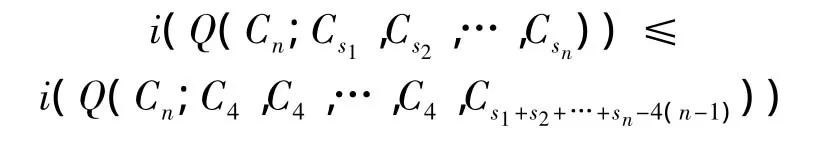
并且等式成立当且仅当

证明 由引理4和定理1，我们得到

同理得到

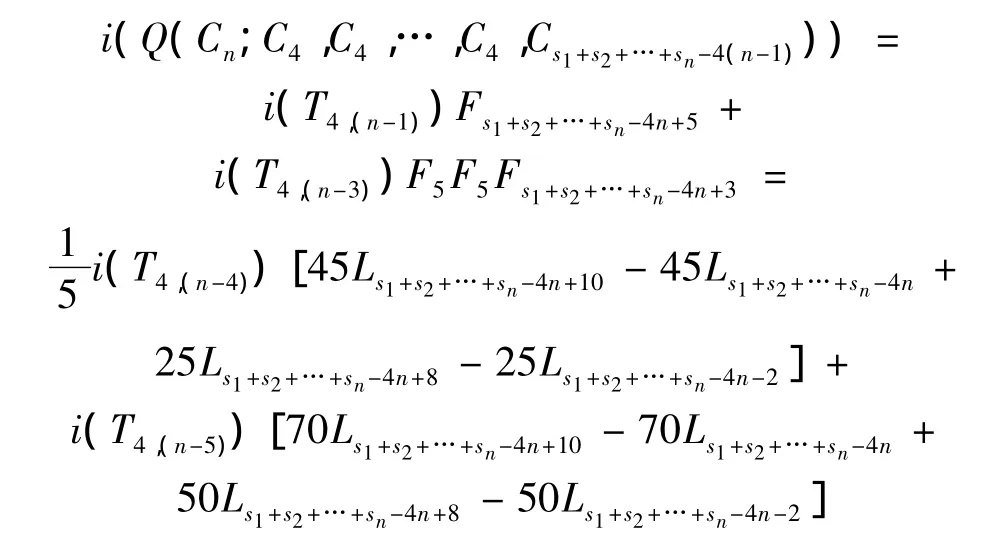
因此

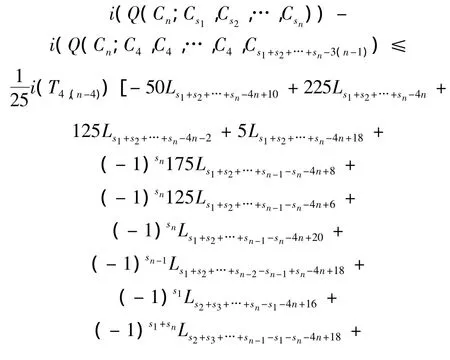
并且等式成立当且仅当Q(Cn;Cs1，Cs2，…，Csn)≅Q(Cn;C3，C3，…，C3，Cs1+s2+…+sn－3(n－1))。

在证明过程中，用到的符号标记T4，k=Q(Pk;C4，C4，…，C4)(k=1，2，…，n)，因此结论成立。

定理3 假设s1，s2，…，sn都是正整数且满足si≥3(i=1，2，…，n)，在顶点数为定值时，则有

并且等式成立当且仅当

证明 由引理2、定理1和定理2，可以得到

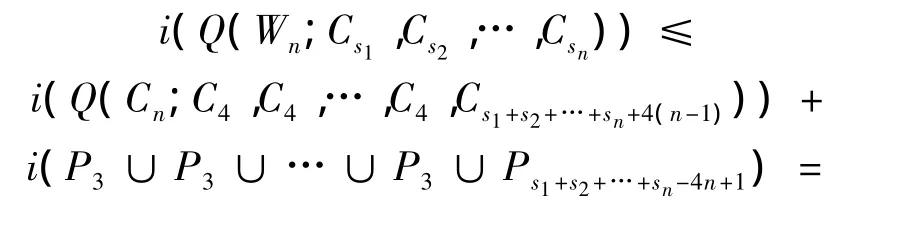
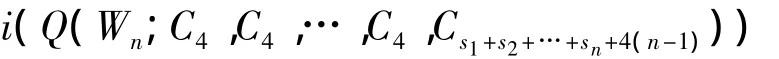
所以定理3成立。

［1］ZHAO H，LI I.On the Fibonacci numbers of trees［J］.Fibonacci Quart，2006，44(1):32 －38.

［2］PRODINGER H，TICHY R F.Fibonacci numbers of graphs［J］.The Fibonacci Quart，1982，20(1):16 －21.

［3］REN S Z，HE W S.The study of σ index onQ(Pk;Cs1，Cs2，…，Csk)graphs［J］.SCIENTIA MAGNA，2008，4(4):40－45.

［4］REN S Z，HE W S.The Merrifield－Simmons index in(n，n+1)－graphs［J］.SCIENTIA MAGNA，2009，5(2):6－14.

［5］REN S Z.Merrifield－Simmons index of tree－type hexagonal systems［J］.MATCH Commun Math Comput Chem，2011，66(3):837－848.

［6］REN S Z，HE W S.The study of σindex onQ(Sk;Cs1，Cs2，…，Csk)graphs［J］.SCIENTIA MAGNA，2008，4(2):49－55.

［7］GUTMAN I，CYVIN S J.Introduction to the theory of Benzenoid hydrocarbons［M］.Berlin:Springer，1989.

［8］SHIU W C.Extremal Hosoya index and Merrifield－Simmons of hexagonal spiders［J］.Discr Apple Math，2008，156(1):2978－2985.

［9］BONDY J A，MURTY U S R.Graph theory with application［M］.New York，1976.