可视化析取时态推理器的设计与实现*

刘越畅，林晓骏，汤 庸

(1.嘉应学院计算机学院，广东 梅州 514015；2.华南师范大学计算机学院，广东 广州 510631；3.华南理工大学计算机学院，广东 广州 510006)

人工智能规划(或称自动规划：automated planning)是人工智能领域一个重要的研究子领域。经典的智能规划依赖于几个理想化假设[1]，如：动作的效果是确定的，系统是静态、完全可观察的，动作是瞬时发生的(动作没有持续时间)，等等。随着解决实际问题的需要和智能规划技术研究的深入，这些理想化假设不再是必需的。例如，现实中的动作或者活动极少是瞬间发生的，往往具有一定的持续时间；另外，动作发生的前提条件不一定非得在动作开始执行时成立，同时动作的效果也不一定都发生在动作完成之时。再如，系统的初始条件和目标命题也可以赋以时间上的意义：初始条件命题可以发生在某个时间段内，而目标命题之间也可以有时间上的关系(时态扩展目标)，等等。此外，引入时间元素还可以对经典规划进行进一步的扩展，如引入外部事件等。时态规划便是经典智能规划对命题和动作在时间的维度上进行扩展的产物。析取时态问题(Disjunctive Temporal Problem, DTP)是Kostas Stergiou和Manolis Koubarakis提出的基于时间点的定量时态模型[2]。使用DTP作为时态规划中的时态模型的优势是可以将规划阶段的决策推迟到调度(时态推理)阶段解决，这样平衡两方面计算量的同时提高了规划灵活性[3]。自DTP问题提出以来，研究者陆续提出了DTP求解算法(如局部搜索DTP算法[4]、基于电路编码的SAT算法[5])、基于拓扑信息的启发式技术[6]，以及DTP问题的扩展(如动态DTP[7]、基于偏好的DTP[8]、多智能体DTP[9])。DTP丰富的表达力和应用潜力使得人们对它的研究持续升温，短短时间内国际著名的人工智能研究杂志《人工智能》已有多篇专门研究DTP的论文诞生。

基于结构信息在DTP问题求解中的重要性，在析取时态网络(Disjunctive Temporal Network, DTN)[10]的基础上，本文提出了DTP弱蕴含性和弱演化析取时态网络(Weakly Evolutional DTN, WEDTN)，设计了基于WEDTN的可视化DTP求解器TRSE(Temporal Reasoning Solution Environment)。系统演示可以看出，与常用的基于搜索树的可视化求解系统不同，基于WEDTN的DTP求解器可视化更有利于人们直观了解DTP的结构特征及其与求解过程的影响。

本文组织如下：第1节首先给出必要的问题定义；第2节介绍DTP问题求解的基本算法及TRSE系统设计；第3节是系统演示部分；第4节介绍相关结论和未来工作。

1 问题定义

定义1 一个简单时态问题(Simple Temporal Problem, STP)[11]是一个二元组，其中：X={x1,x2, …,xn}称为时态变量集合；C={c1,c2, …,cm}是简单时态约束集合，每个ci是形如xi-xj≤c(xi,xj∈X，c∈Z)的二元约束1。

由定义可知，一个STP与一个所有变量定义在整数域上的约束满足问题(Constraint Satisfaction Problem, CSP)是等价的。正如CSP可以使用约束图来表示那样，STP也可以使用时态约束网络来表示，下面给出具体定义。

定义2 给定一个STP，其简单时态网络是一个有向边标号图，其中：V={vi|xi∈X}，E={|xi-xj≤c∈C}，W是一个权重函数W:E→Z，使得：任意xi-xj≤c∈C则W()=c。

定义3 一个析取时态问题是一个二元组P=，其中：X={x1,x2, …,xn}是一个变量集合；C={C1,C2, …,Cm}是一个约束集合，每个Ci是一个形如ci1∨ci1∨…∨cik的析取式(也称为子句)，可以表示为集合{ci1,ci1, …,cik}，其中的cij是一个形如xu-xv≤c的简单时态约束(xu,xv∈X；xu,xv,c∈Z)。

定义4 给定一个析取时态问题P=，它相应的析取时态网络是一个五元组N=，其中：V(N)={v1,v2,…,vn}是顶点集合；E(N)={|vi,vj∈V(N),k∈L,w∈W}是一个四元组边集合；L={k|Ck∈C}是一个标号集合；W是一个权重符号集合；PRJ是个映射函数，使得：PRJ(xi)=vi(xi∈X)，PRJ(ck=xi-xj≤c)=。

由DTN的定义可以看出，一个DTN实际上是一个有向、多重标号图。

性质1 给定一个DTP=，其中：X={x1,x2, …,xn}，C={C1,C2, …,Cm},P是一致的，当且仅当存在一个一致的STP, (C’={c1,c2, …,cm},ci∈Ci)。这样的STP通常称为析取时态问题的解STP。

图1给出了DTP及其DTN的示例[10]。

性质2 给定DTPP=和P’=,称P’弱蕴含P，如果X=X’ ,C’⊂C，且P’是一致的⟹P是一致的。DTN之间的弱蕴含关系等价于它们相应的DTP的弱蕴含关系。

定义5 给定一个初始DTN，N0，和另一个DTN，N1，N1是N0关于边e的弱演化DTN(Weakly Evolutional DTN, WEDTN)，如果N1=N0-{e’|N0(L)(e’)=N0(L)(e)}且N1弱蕴含N0。

图2是弱演化DTN序列的示意图。

图2 弱演化DTNFig.2 Weakly evolutional DTN

弱演化DTN实际上考察了在搜索过程中DTN随着变量赋值的进行对原变量未选值从原DTN中删除后的演变过程。也就是说，DTP求解问题变为寻找一个原问题DTN的弱演化DTN的解STP的过程。

2 算法及系统设计

2.1 DTP一致性判定算法

根据性质1，一个DTP是否是一致的，可以应用搜索算法查找解STP来求解。此时相当于将原问题看作一个CSP：每个变量对应于DTP中的每个析取约束，而变量的取值范围是该析取约束中的所有析取肢(即简单时态约束)；而约束则要求所有变量的取值构成一个一致的简单时态问题(即解STP)。

图3给出了该CSP求解算法的大体框架[12]。该算法每次选择一个变量(第2行)进行尝试赋值，若当前赋值与当前部分解一致(第4行)则进行下一轮迭代(第5行)；否则尝试其它的值。

图3 DTP求解搜索算法Fig.3 Search algorithm for DTP solution

2.2 启发式(Heuristics)技术

DTP的求解与CSP的求解一样，实际应用中必须使用一些启发式技术，否则必定遭遇状态爆炸的问题。当前研究文献中提出的求解DTP的启发式技术主要有前向检查技术、最少剩余值变量排序、语义分枝、被吸收变量移除、递增前向检查技术、基于拓扑的变量、值选择策略等。以下对这些技术的基本思想作简要介绍。

2.2.1 前向检查(Forward Check, FC) 前向检查技术的核心思想在于：在尝试赋值之前，首先从未赋值元变量的取值域中删除那些与当前部分解不一致的元值。这种技术的优点在于可以在进行下一轮迭代之前首先发现搜索的死点(如果前向检查过程中某个元变量的取值域为空)，从而可以提前回溯，避免进行下一轮迭代。

2.2.2 最少剩余值(Minimal Remaining Values, MRV) 最少剩余值策略的主要思想在于：在当前节点选择变量(FC_DTP中的select_var函数)进行当前赋值的时候，优先选择那些具有最少候选元值的元变量。MRV策略是一种最常使用的基于“失败优先(FF)”原则[13]的变量选择策略。与前向检查技术配合使用时，由于元变量的取值域随着搜索的进行不断地发生变化，因此MRV实现了动态的变量选择功能。实验证明FC与MRV的组合具有显著的剪枝能力[14]。

2.2.3 语义分枝策略(Semantic Branching, SB)

语义分枝策略也是DTP求解中的一个剪枝能力很强的启发式技术。它的核心思想是：在针对某个变量赋值的搜索节点，若一个值(cij:x-y≤c)尝试后到达一个死点，该值将被抛弃并将尝试其它的值；此时，根据该不等式的语义，在当前DTP和部分解下，x-y≤c为假意味着～(x-y≤c)即x-y>c为真，在时态变量取值为整数的情况下有y-x≤-c-1为真，将y-x≤-c-1显式地加入到当前部分解中并将该约束传播不会改变原问题的一致性，并将有助于更早地剪枝。

2.2.4 被吸收变量移除技术(Removal of Subsumed Values, RSV) 被吸收变量移除技术的思想是：假设当前部分解STP的距离图中，有x、y之间的最短距离distance(x,y)=c，如果对于某个未赋值的元变量Ck其取值域中具有一个候选元值ckj：y-x≤c’且有c≤c’，则称Ck被该解STP所吸收；此时可直接将ckj：y-x≤c’赋值给Ck而不需要进行一致性判定和尝试其它的值(因为此时ckj：y-x≤c’的加入不会使最短距离发生任何变化，因此它与当前部分解STP必然是一致的。

2.2.5 基于拓扑的变量和值选择策略(Topology-based Variable/Value Ordering, TVO) TVO的基本思想是：从DTN中计算每条边的冲突系数，通过多种组合函数，计算每个变量的冲突系数。根据冲突系数和“失败优先”(Fail-First)原则，优先选择那些冲突系数较大的变量和冲突系数较小的值。虽然同样是变量选择策略，实验证明TVO比MRV具有更强的剪枝能力[6]。

2.3 系统设计

TRSE系统架构如图4所示。其中：Script模块主要是DTP问题的表示脚本。该脚本传递给系统的Model(建模)模块，生成问题的内部表示。Model模块将问题信息分别与Engine和Visulisation模块交互，完成问题的求解及可视化。以下分别阐述各模块的设计。

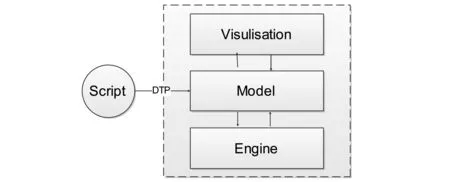
图4 TRSE系统架构Fig.4 TRSE architecture

2.3.1 建模(Model)和引擎(Engine)模块 将DTP问题放在CSP的框架下求解最大的优势是，可以使用大量现有的CSP研究成果应用到DTP的求解中。其次，应用现有优秀的CSP求解框架能够使整个求解器结构清晰，易于使用和维护。为了达到这个目的，本文使用Gecode作为建模和求解引擎。Gecode是瑞典皇家理工学院Christian Schulte开发的开放、免费、可移植、易使用、有效率的用于开发基于约束系统及应用的环境约束求解框架，它提供一个模块化和可拓展的约束求解器。图5展示了Gecode的系统架构[15]。

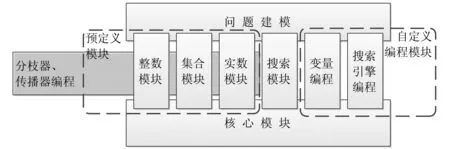
图5 Gecode系统架构Fig.5 Gecode architecture

从Gecode架构设计可见，除了提供预先定义的常见类型变量(整数、实数、集合类型)及相关约束，Gecode还提供了丰富的自定义编程(Programming)功能，使用户可以根据自己的需要对用户领域的约束满足问题进行灵活建模。对DTP的可视化约束满足建模要对其中的变量、传播器和分枝器、搜索引擎分别进行自定义编程。由于约束建模可以有多种灵活的方式，对同一个DTP，Gecode同样提供多种建模方法。在本系统中，为方便起见，我们仍然应用整数变量类型处理。使用Map数据结构将每个整数值与相应的简单时态约束联系起来。

根据这一架构，在TRSE系统中设计了以下的分枝、传播器。

1) 分枝(Brancher)策略。

根据以上对应用的启发式策略分析，其中的MRV和TVO分别可以作为不同的分枝器。连同最简单的变量随机选择方法，系统中设计了三种分枝器：BaseBrancher、MRVBrancher、TVOBrancher。需要注意的是，这三种分枝器是互斥的，即每次约束求解进行的时候，只能应用其中一种分枝器。

其结构如图6。

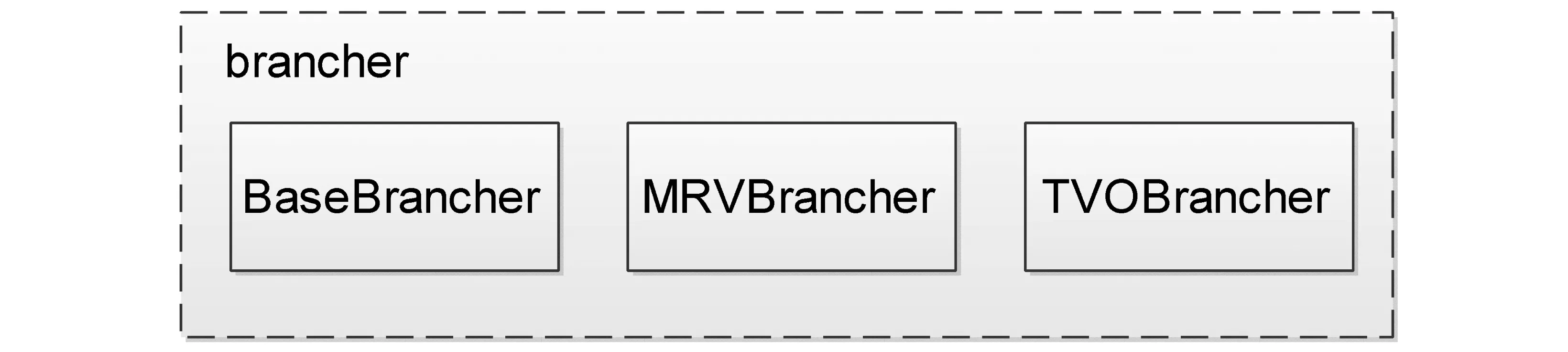
图6 分枝器类设计Fig.6 Brancher classes design

2) 传播器(Propagator)。

在Gecode框架中，传播器可以对两种元素进行描述：一种是约束，以判定当前值选择的一致性；另一种是约束的传播，以进行搜索的剪枝。本系统设计了以下传播器：FWPropgat/DPCPropgat/PC3Propgat是第一种传播器，用以判断当前部分解STP的一致性(分别对应FloydWarshall算法、DPC算法[11]、P3C算法[16])，这三个有且仅有一个在运行中起作用；FCPropgat/RSVPropgat/SBPropgat是第二种传播器，对应于前面描述的三种启发式：前向检查、被吸收变量移除、语义分枝，此三种传播器可以在约束求解前任意选择是否在求解中应用。传播器的设计如图7所示。

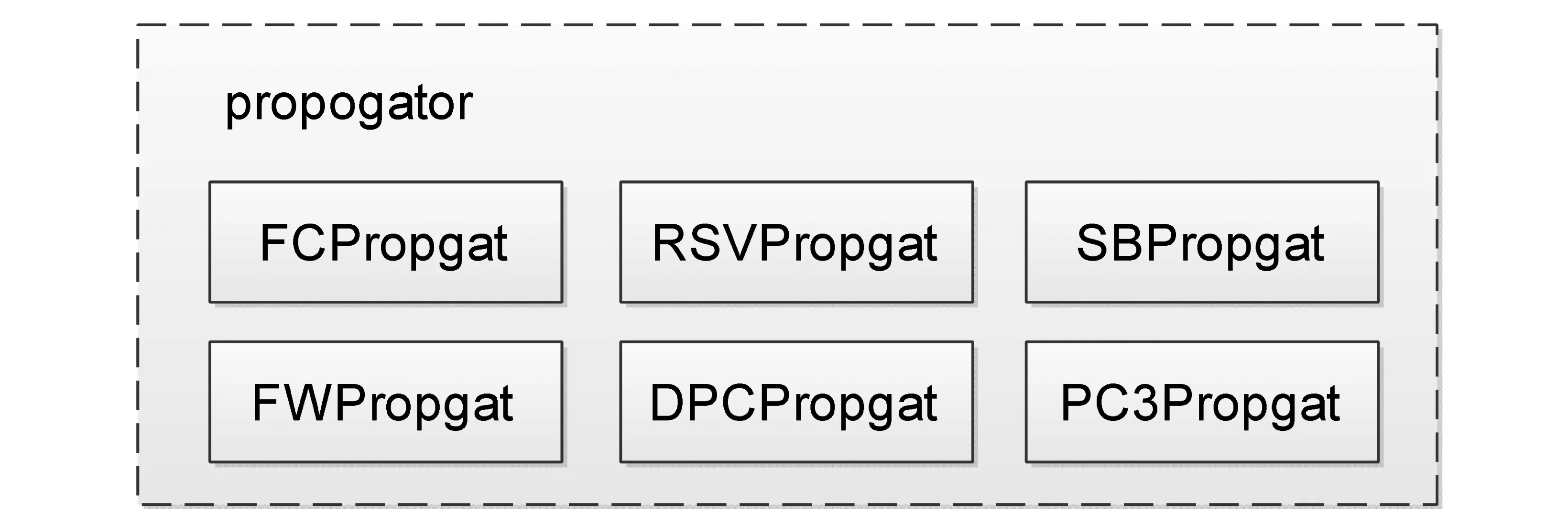
图7 传播器类设计Fig.7 Propagator class design

③ 引擎编程(Engine programming)

通过分枝器和传播器，利用Gecode缺省的算法引擎已经能够处理大多数的约束求解及应用。在TRSE中，可视化模块要求跟踪引擎的运行过程，以便将求解过程(主要是变量赋值信息)进行图形化展示。因此，需要对引擎进行变量选择并赋值后，将该信息传递给可视化模块进行图形展示。这主要在Status()函数中调用choice()函数获得。

图8展示了以上设计的分枝器和传播器交替执行的迭代过程。一个基于CSP的DTP求解过程主要就是分枝和传播的迭代过程，在这个过程中，首先进行分枝(即：变量和值选择)，然后根据分枝结果进行约束的传播为下一次分枝做准备。此过程也考虑了多个分枝器和传播器的相容性问题：MRVBrancher、TVOBrancher和BaseBrancher每次需要且只能选择其中之一，FCPropogat默认使用，RSV和SB传播器可同时使用，用于STP简单约束传播的P3C、DPC、FW传播器次需要且只能选择其中之一。

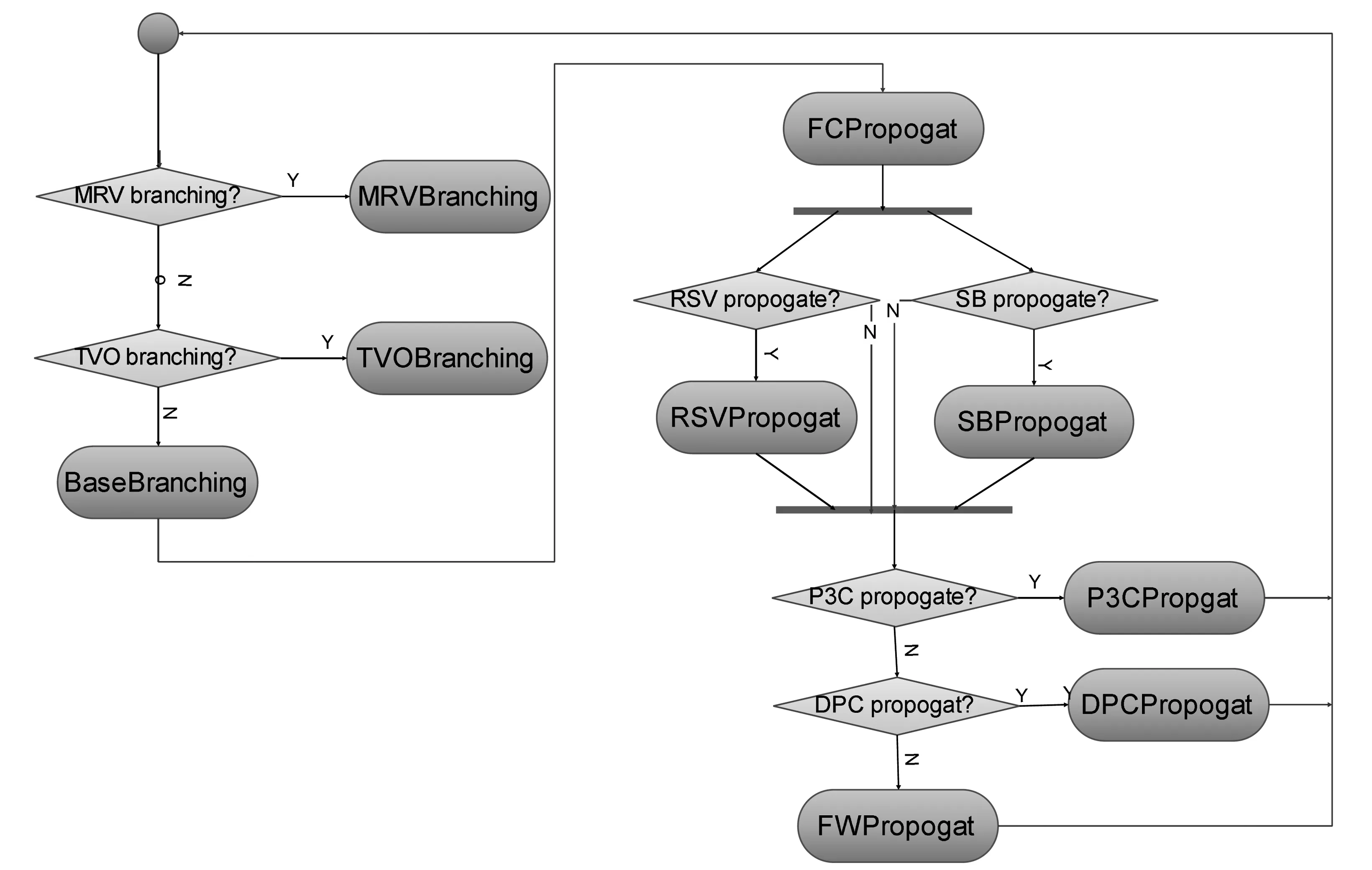
图8 分枝器和传播器交替执行过程Fig.8 Iterative execution of branchers and propagators

2.3.2 可视化(visualisation)模块 与Gecode现有的Gist可视化模块(仅表达搜索过程中节点选择的搜索树)不同，TRSE中的可视化模块使用DTN表达问题的拓扑结构，并在此结构上动态展示搜索中的动态值选择过程。内部图结构使用JGraphT[17]，而图形展示使用开源的JUNG库[18]实现。

3 系统实现及演示

图9是TRSE系统界面。该系统分为四大模块。一是输入模块，可以通过文本框键盘输入、选择一个DTP文件或者选择目录顺序求解该目录下所有DTP文件三种方式输入求解对象。二是选项设置模块，用于进行求解前的设置选项(使用的分枝器、传播器、超时设置、可视化设置)。三是可视化显示模块，用于通过演化DTN动态展示求解过程。四是结果输出模块，展示DTP求解结果。

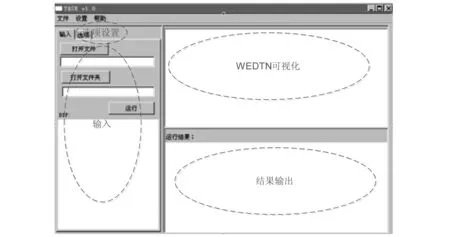
图9 TRSE主界面Fig.9 TRSE graphical user interface

示例：假设输入DTP：P=,X={x1,x2,x3,x4,x5},C={C1,C2,C3}。C1≡x1-x2≤2 ∨x3-x2≤-1；C2≡x2-x3≤2 ∨x1-x2≤4；C3≡x2-x1≤-3 ∨x3-x1≤-5。

选择BaseBrancher分枝器，不选择除FCPropgat之外任何传播器进行问题求解，可视化模块将按图10形式动态显示DTN演化过程。

4 结 语

由于析取时态问题在智能规划和调度领域中广泛得到应用，近年来成为该领域的研究热点，已产生了多篇国际《人工智能》杂志上发表的研究论文。本文阐述了一个以DTP为模型的通用时态推理系统TRSE的设计和实现。TRSE的设计充分采用软件设计模式和基于演化DTN的可视化设计，运用现有的高效CSP求解器Gecode和图可视化库JUNG，将重点放在各种启发式技术的设计和动态可视化上。虽然DTP的理论研究已经取得了较大进展，目前尚未有此类通用推理系统的研发，基于WEDTN的可视化技术解释了DTP求解中的结构特性，对于DTP乃至时态推理的学习、研究有重要的价值。进一步的工作将扩展对其他DTP求解技术的集成和已探索DTN和未探索DTN空间[12]等更细致的结构特征的展示支持。

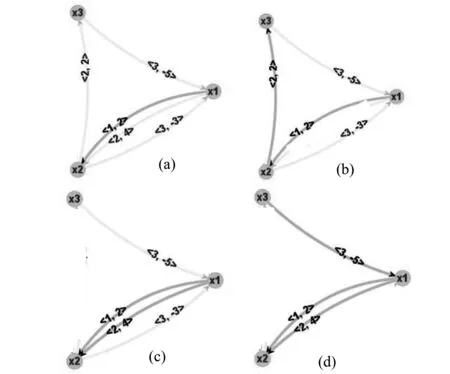
图10 DTN弱演化过程((a)→(b)→(c)→(d))Fig.10 Weak evolution process((a)→(b)→(c)→(d))

参考文献：

[1] GHALLAB M, NAU D, TRAVERSO P. Automated planning: theory and practice [M]. San Francisco: Morgan Kaufmann Publishers, 2004.

[2] STERGIOU K, KOUBARAKIS M. Backtracking algorithms for disjunctions of temporal constraints [J]. Artificial Intelligence, 2000, 120(1): 81-117.

[3] LIU Y, FANG Y. Boost the Integration of planning and scheduling: a heuristics approach [J]. Procedia Engineering, 2012, 29: 3348-3352.

[4] MOFFITT M D, POLLACK M E. Applying local search to disjunctive temporal problems [C]// IJCAI, 2005: 242-247.

[5] BLAINE NELSON T K S K. CircuitTSAT: a solver for large instances of the disjunctive temporal problem [C]//The Eighteenth International Conference on Automated Planning and Scheduling, ICAPS 2008, Sydney, Australia, 2008: 232-239.

[6] LIU Y, JIANG Y, QIAN H. Topology-based variable ordering strategy for solving disjunctive temporal problems[C]//In 15th International Symposium on Temporal Representation and Reasoning, 2008. TIME ’08, 2008: 129-136.

[7] SCHWARTZ PETER J, POLLACK MARTHA E. Two approaches to semi-dynamic disjunctive temporal problems[C]//ICAPS Workshop on Constraint Programming for Planning and Scheduling, Monterey, California, USA. June 2005.

[8] MOFFITT M D. On the modelling and optimization of preferences in constraint-based temporal reasoning [J]. Artificial Intelligence, 2011, 175(7/8): 1390-1409.

[9] BOERKOEL JR J C, DURFEE E H. A distributed approach to summarizing spaces of multiagent schedules [C]//In Proceedings of the 26th National Conference on Artificial Intelligence (AAAI-12), Toronto, Canada, 2012: 1742-1748.

[10] 刘越畅，姜云飞，钱红. 基于问题结构的启发式策略在析取时态问题求解中的应用 [J]. 计算机研究与发展，2008, 45(11): 1840-1849.

[11] DECHTER R, MEIRI I, PEARL J. Temporal constraint networks[J]. Artificial Intelligence,1991,49:61-95.

[12] 刘越畅. 基于约束的时态推理和时态规划[D]. 广州: 中山大学, 2008：75-99.

[13] HARALICK R M, ELLIOTT G L. Increasing tree search efficiency for constraint satisfaction problems [J]. Artificial Intelligence, 1980, 14: 26-31.

[14] TSAMARDINOS IOANNIS, POLLACK MARTHA E. Efficient solution techniques for disjunctive temporal reasoning problems [J]. Artificial Intelligence， 2003, 151(1/2): 43-89.

[15] SCHULTE C, TACK G, LAGERKVIST M Z. Modeling and programming with Gecode [EB/OL]. [2010] http://www.gecode.org/doc/4.2.0/MPG.pdf.

[16] PLANKEN L, WEERDT M D, KROGT ROMAN VAN DER. P3c: a new algorithm for the simple temporal problem [C]//In Proceedings of the International Conference on Automated Planning and Scheduling (ICAPS 2008), 2008: 256-263.

[17] JgraphT.A free Java graph library [EB/OL]. [2013] http://jgrapht.org.

[18] JUNG. Java universal network/graph framework [EB/OL]. [2013] http://jung.sourceforge.net.