一类复杂系统模型的动力特性及广义控制*

李 银，位瑞英

(1. 韶关学院数学与信息科学学院，广东 韶关 512005；2.中山大学数学与计算机学院，广东 广州 510275)

复杂系统在保密通信、激光物理、化学反应等领域有巨大应用潜力[1-6]。人们不断发现新的复杂系统，研究其分叉、混沌现象、混沌吸引子结构和混沌产生的条件等动力特性与控制问题．如同步控制、模糊控制、反馈控制等[7-13]。

本文针对复杂系统模型的动力特性特性作进一步探讨，利用射影同步控制方法实现该系统的广义同步控制，并利用Maple数值仿真试验，得到有效非线性控制器，验证了其方法的有效性。

1 一类复杂系统模型及其动力特性分析

考虑复杂系统模型[7]：

(1)

(x,y,z)T∈R3为系统的状态变量，当选取a=6,c=-4时，系统处于混沌状态。

1.1 复杂动力性

系统在变换(x,y,z)→(-x,-y,z)下，对所有的参数值保持不变性，具有对称性。系统模型振荡的复杂性和随机性演化时序图如图1。

图1(a)，(b) ，(c)分别表示初值(x(0),y(0),z(0))=(3,-4,2)时，x，y和z是随时间变化的曲线。 由图可知，系统变量具有复杂性和随机敏感性。

1.2 耗散性

对于系统(1)，计算向量场的散度

故系统(1)是耗散的。体积元V(0)在时间t时收缩为体积元V(0)e-10t，当t→∞时，包含系统轨线的每个小体积元以指数速率10收缩到0，这就意味着系统的动力学行为最终趋向于一个吸引子，该奇怪吸引子形成过程如图2。

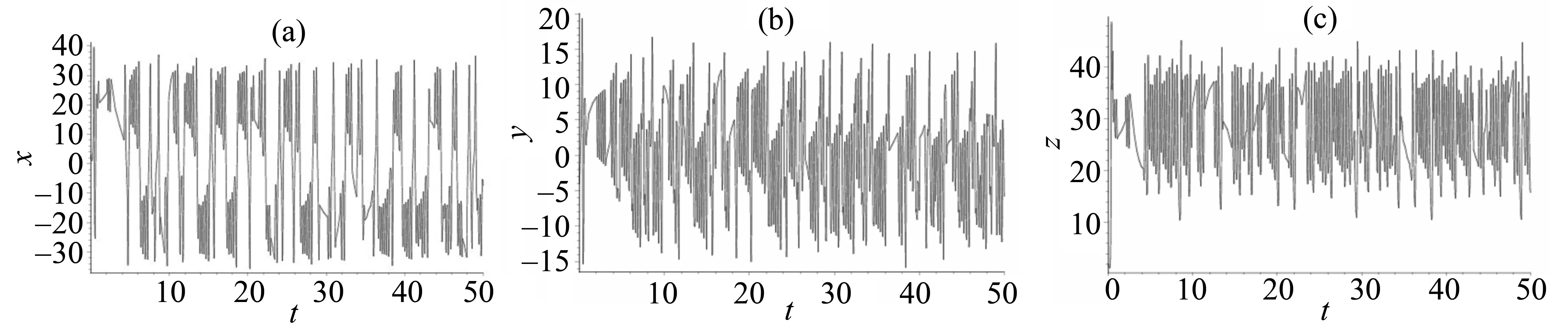
图1 复杂性和随机性Fig.1 Complex complexity and randomicity

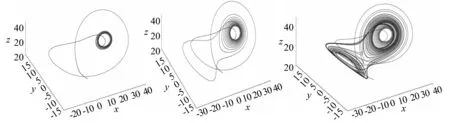
图2 系统模型(1)奇怪吸引子形成的渐进过程Fig.2 System model (1) strange attractor formation of gradual process

1.3 李雅普诺夫指数与分形维数

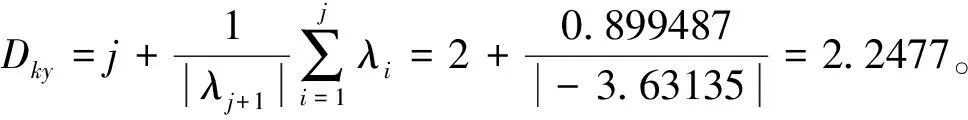
2 平衡点及其稳定性

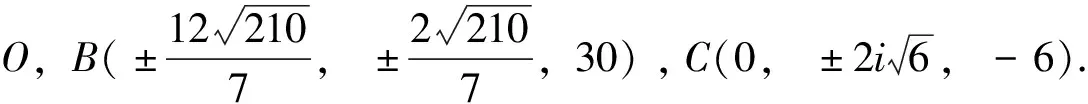
定理1 (Routh-Hurwitz定理)特征方程：λI-A=λn+a1λn-1+....+an-1λ+an=0, 其中I∈Rn×n单位矩阵，A为的实矩阵，若系数满足Δi>0(i=1,2,...,n):

那么特征方程的所有特征值都具有负实部。

命题1 当参数满足a=6,c=-4时，系统 (1) 的平衡点O(0,0,0)是不稳定的。

证明系统(1) 在平衡点O(0,0,0) 的Jacobi矩阵为

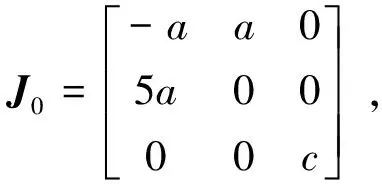
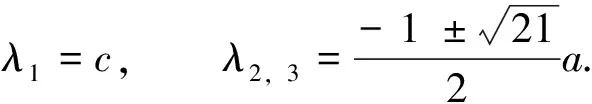
(2)

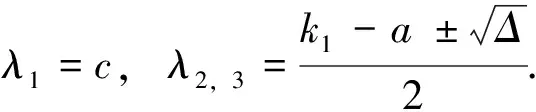
k1=4, (x,y,z)=(3,-4,2)。 图 3(a-c)为被控系统的动力学行为，控制器也可取其它函数等[6]。

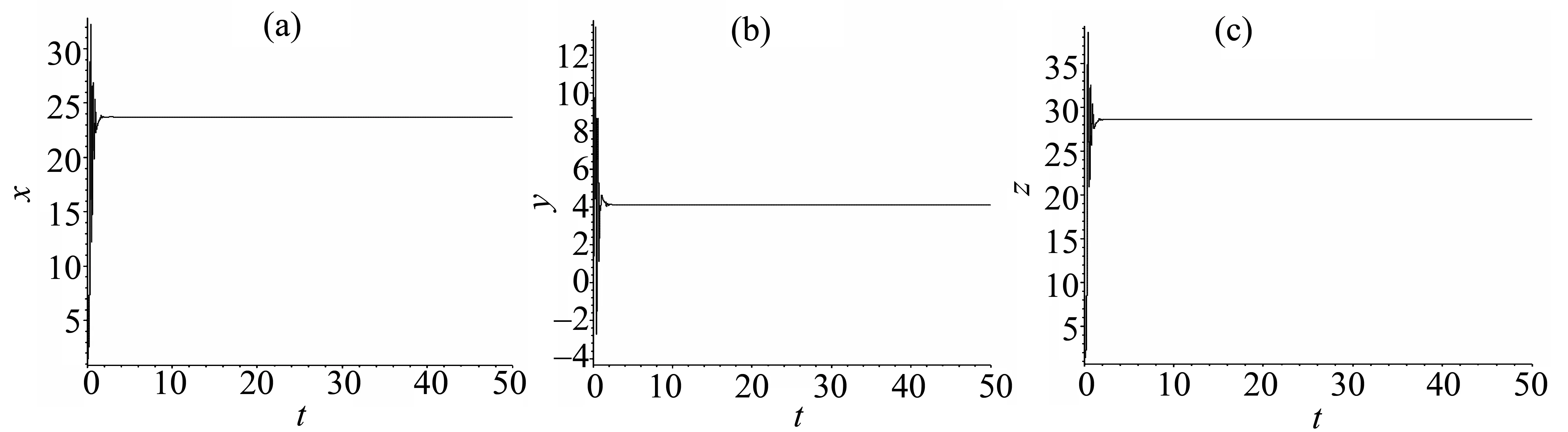
图3 (a) (x, t) 轨迹；(b) (y, t) 轨迹; (c) (z, t) 轨迹Fig.3 (a) (x, t) orbit;(b)(y, t) orbit; (c) (z, t) orbit

3 系统模型(1)的广义控制

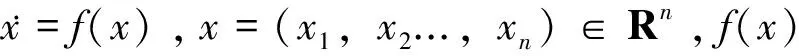
定理2 若定义1中g(y)满足Lipschitz连续条件，控制器被设计

u=M-1f(x)-M-1(A-α)e-

(3)

而α=diag(α1,α2......αn),且满足min(αi)>(LB+A)，则(1)和(2)广义同步控制。

证明误差系统：e(t)=x-My。 由定义1和(3)式知

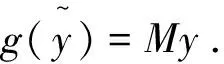
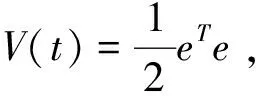
(A+LB-min(αi))e2

(4)

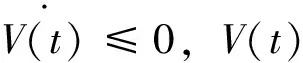
由于复杂系统对初值的敏感性, 即使结构相同的2个复杂系统, 因初值不同, 运动轨迹也会产生很大的差别。以下设计并实现同步控制。系统(1)写成如下:

(5)

假设系统(5)为驱动系统，构造响应系统

(6)

u1,u2,u3为所要设计的控制器。令e1=x1+α1x2,e2=y1+α2y2,e3=z1+α3z2，得到误差

(7)

根据(3)式设计如下控制器函数

将式(8)代入系统(7)，原误差系统简化为

(9)

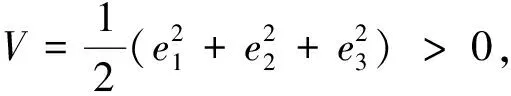
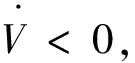
由图4知, (a),(b),(c) 展示了ei(i=1,2,3)的变化规律。图5为同步曲线。

图6分别是系统模型同步吸引子与相图。由图5-6可知，在极短的时间内实现了复杂系统的广义同步控制，达到系统变量快速跟踪。

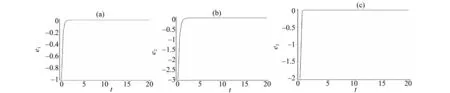
图4 误差状态：(a) e1=x1+α1x2；(b) e2=y1+α2y2; (c)e3=z1+α3z2Fig.4 The error states: (a)e1=x1+α1x2; (b) e2=y1+α2y2(c)e3=z1+α3z2

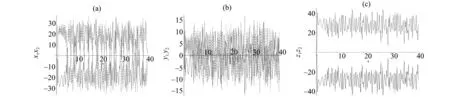
图5 跟踪状态：(a) 红x1与 蓝α1x2(b) 红y1与 蓝α2y2; (c) 红z1与 蓝α3z2Fig.5 Tracking states: (a) the redx1and the blue α1x2;(b)the redy1 and the blue α2y2; (c) the redz1 and the blue α3z2

图6 混沌吸引子和相图(红驱动系统，蓝响应系统)(a)(x,y,z)空间，(b) x-y平面; (c) x-z平面; (d) y-z平面Fig.6 Chaotic attractor and phase figure (the red is the drive, the blue is the response)(a) (x,y,z)space; (b) (x,y) phase; (c) (x,z) phase; (d) (y,z) phase

4 结 语

本文将数值计算、稳定性分析及非线性控制三者相结合，分析了一类复杂系统的动力特性。基于稳定性和控制理论，给出一类新控制器，实现了该模型的全局控制，而且实现同步的时间比较短，是实现系统模型控制的有效方法。

参考文献：

[1] 王光瑞,于熙龄,陈式刚.混沌的控制、同步与利用[M]. 北京:国防工业出版社, 2001.

[2] 关新平等.混沌控制及其在保密通信中的应用[M]. 北京:国防工业出版社, 2002.

[3] 陈红兵.一类具有收获率互惠系统的稳定性及Hopf分岔[J]. 中山大学学报：自然科学版, 2013，52(1):45-50.

[4] GOPALSAMY K. Stability and oscillations in delay difernetial equations population. dynamics[M].Kluwer Academic: Dordrecht, 1992:22-33

[5] PECORA L, CARROLL T. Synchronization in chaotic systems[J].Phys Rev Lett，1990，64:821-827.

[6] LI Y, LI B. Chaos control and projective synchronization of a chaotic Chen-Lee system[J].Chinese Journal of Physics，2009，47: 297-306.

[7] XIE C, XU Y, Chaos control and synchronization of a complex chaotic system[J]. IWCFTA，2010：1：71-76.

[8] 王瑞萍.基于分数阶PD控制器的永磁同步电动机控制[J].中山大学学：自然科学版,2013，52 (3): 34-39.

[9] LI Y, CHEN Y, LI B. Adaptive control and function projective synchronization in 2D discrete-time chaotic systems[J]. Commun Theor Phys, 2009，51: 270-281.

[10] LI Y, CHEN Y, LI B.Anticipated function synchronization with unknown parameters in discrete-time chaotic systems[J]. International Journal of Modern Physics C, 2009， 20:597-608.

[11] CHENY, AN H L, LI Z B. The function cascade synchronization approach with uncertain parameters or not for hyperchaotic systems[J]. Appl Math Computer，2008，197:96-108.

[12] LI X. Function projective synchronization of two identical new hyperchaotic systems[J].Comm in theor Physics, 2007， 48:864-873.

[13] LI Y, ZHENG C L. The complex network synchronization via chaos control nodes[J]. Journal of Applied Mathematics, 2013， 63 :1-12.