双散射环境下互耦对多入多出系统容量的影响

李岳衡 彭文杰 燕 璐 居美艳 黄 平

(河海大学计算机与信息学院，江苏 南京 211100)

引 言

多入多出(Multiple Input and Multiple Output，MIMO)多天线收发技术是新一代绿色无线通信系统中实现高速数据传输的关键技术之一. 已有研究结果表明[1]，收发端散射环境导致的阵列接收信号空域相关性会对MIMO系统容量产生显著影响. 对于收发两端皆使用天线阵列的多天线系统，随着整个系统尤其是移动终端日渐小型化的发展需求，天线阵元间的互耦效应已不可避免地成为影响阵列空域相关性和系统容量的重要因素[2-3]. 在已发表的研究成果中，文献[4]初步给出了互耦对MIMO信道空域相关性及系统容量的影响；文献[5]报道了多元阵列天线间的互耦对MIMO系统容量的影响，但仅考虑了接收端天线存在互耦效应的情形. 这些研究虽然分析了天线单元间互耦可能对空域相关性的影响，不过其所采用的信道模型都是基于简单独立同分布的瑞利衰落模型，故不具普遍性和现实性.

显然在具体考虑互耦效应对MIMO系统性能影响之前，选择或者建立一个合适的MIMO传输信道是非常有必要的，如此则可最大程度地模拟互耦效应对实际MIMO通信系统的功用，并在此基础上对原系统加以改进与完善. 文献[6]给出了一种基于散射效应的非频率选择性Rice衰落几何单反传输模型，但该模型仅适用于发射端天线较高，即其周围不存在阻挡电波传播的障碍物，且散射体只存在于接收端的情形. 显然在实际MIMO信道中，散射体的位置不仅仅位于接收端周围，在发射端周围也应有大量散射体存在. 为此文献[7-8]考虑了更切合实际的散射体位于收发两端的情况，但论文的应用背景是大尺寸MIMO系统，忽略了收发两端天线阵元本身的互耦效应对MIMO系统容量的影响，故其研究结论不适合紧凑型MIMO系统. 文献[9]虽然分析了天线单元间的互耦对室内MIMO无线信道的影响，亦即考虑了散射体位于发射端与接收端的情况，但并没有给出散射体排列等参数对MIMO系统容量影响的具体分析，研究内容不够完善.

1 阵列互耦效应

当两个或者多个天线近距离放置时，天线之间由于电流或电场的耦合会产生相互间的干扰，这种干扰就是所谓的互耦效应. 天线间互耦效应通常用耦合系数矩阵来表征.

图1 阵列互耦网络模型

如图1所示即为阵列互耦网络模型.n元天线阵受来波照射之后在每个阵元上激发电动势Vi1，Vi2，…，Vin；zL1，zL2，…，zLn为负载阻抗，z11，z22，…,znn为天线自阻抗. 由文献[10]的推导过程可知：若耦合系数矩阵在不计互耦时为单位阵，则在考虑互耦时耦合系数矩阵为

(1)

式中：ZL=diag(zLi),(i=1,2，…，n)是负载对角矩阵；In是n维单位矩阵；Z=(zij),(i=1,2，…，n) 是互阻抗矩阵；Zs=diag(zii),(i=1,2，…，n)是自阻抗矩阵. 假设各个天线的自阻抗相等且负载阻抗zL1等于自阻抗的共轭，此耦合系数矩阵可通过以下公式求得[10]：

Cr=(zL1+z11)(ZL+Z)-1.

(2)

以阵元自阻抗z11，以及阵元1和阵元2的互阻抗z12为例，Z矩阵各元素的求法如下[11]：

z11= 30×[0.577+ln(8πl/λ)-ci(8πl/λ)+

jsi(8πl/λ)];

(3)

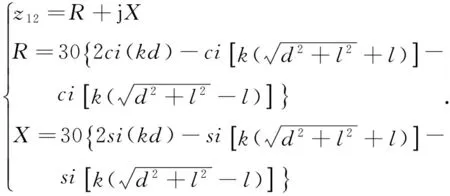
(4)

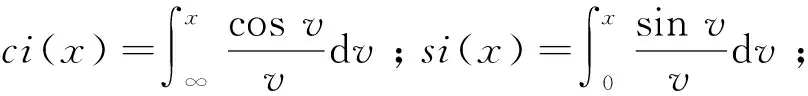
互耦效应最终对整个阵列接收信号的影响可表示为

式中：v=[V1,V2,…,Vn]T为计及互耦效应后天线阵各阵元的接收信号矢量；vi=[Vi1,Vi2,…,Vin]T为不考虑互耦效应时各天线阵元上的接收信号矢量.

2 双散射环境MIMO系统传输特性

2.1 双散射MIMO信道传输模型

在非视距(Non-Line-of-Sight，NLOS)传播中，无线传输信道的两端一般会产生散射衰落. 为研究方便，仅考虑信号为平面波的近场散射MIMO传输模型. 文献[7]最早提出并研究了一个双散射环境MIMO信道传输模型.

如图2所示，发射端和接收端分别由M和N

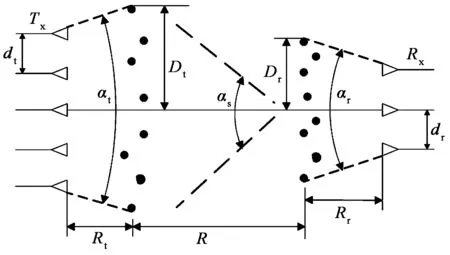
图2 双散射MIMO传输模型

个全方向天线组成线阵，且周围都围绕着大量散射体，以至于无法实现视距(Line-of-Sight，LOS)传输. 假设两端散射半径分别为Dt和Dr，R表示发送端散射体到接收端散射体之间的距离，发送端和接收端天线间距分别为dt和dr，发送端和接收端的角展度分别为αt和αr，αS表示发送端散射体到接收端散射体的角展度，发送端散射体和接收端散射体到各自天线阵的距离分别为Rt和Rr.

在双散射传输模型中，

(6)

(7)

假设收发两端周围的散射体个数都是S，则接收散射体的角展度为

(8)

2.2 信号相关特性分析

据文献[12]可知，存在散射的情况下，天线阵元m和阵元k之间的相关系数可表示为

(9)

式中：p(α)是波达方向的概率密度函数；αr为接收端角展度. 当波达角在[-αr/2，αr/2]区间服从均匀分布时，有近似相关系数公式[7]为

式中：Rαr,dr为N×N阶接收端相关系数矩阵；S(奇数)表示散射体数量； αr,i表示接收端散射线阵第i个散射体发射信号到接收天线线阵的波达角. 若设置参数值：Rt=Rr=50 m，波达方向满足均匀分布时，可得图3所示天线1和天线2之间相关系数随散射体半径变化的曲线.

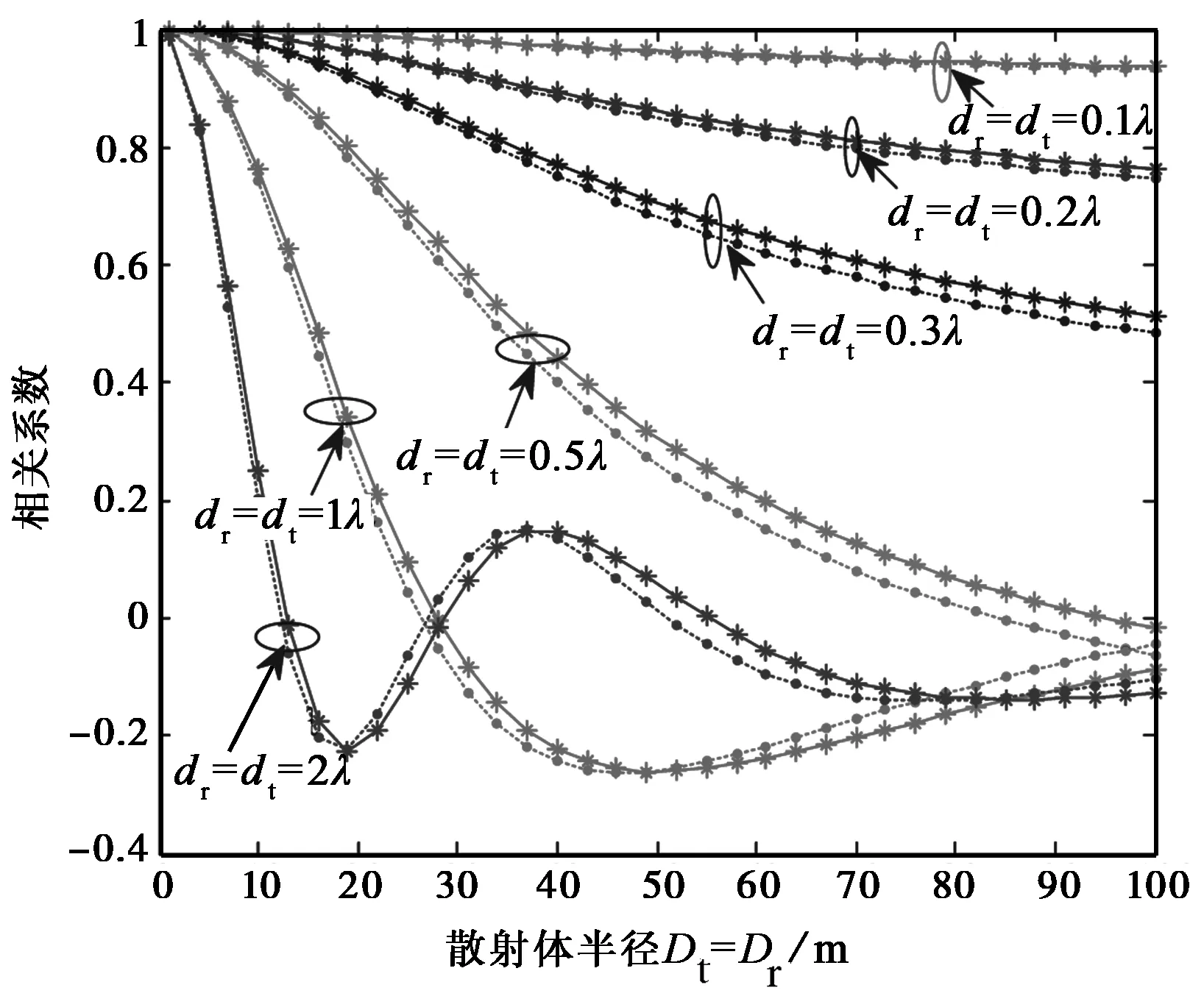
图3 波达方向为均匀分布时相关系数

图3中实线表示由公式(9)所得天线阵元间相关系数的理论值，虚线表示由近似相关系数公式(10)所得的阵元间相关系数的仿真值. 从图3可以看出：当天线间隔小于λ/2时，相关系数随散射体半径的增大而减小，且相关系数值都比较大；当天线间隔大于λ/2时，相关系数刚开始随散射体半径的增大而减小，最后接近于贝塞尔曲线.

若波达方向角服从零均值高斯分布，即波达方向角概率密度函数p(α)满足[12]

(11)

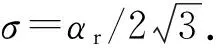
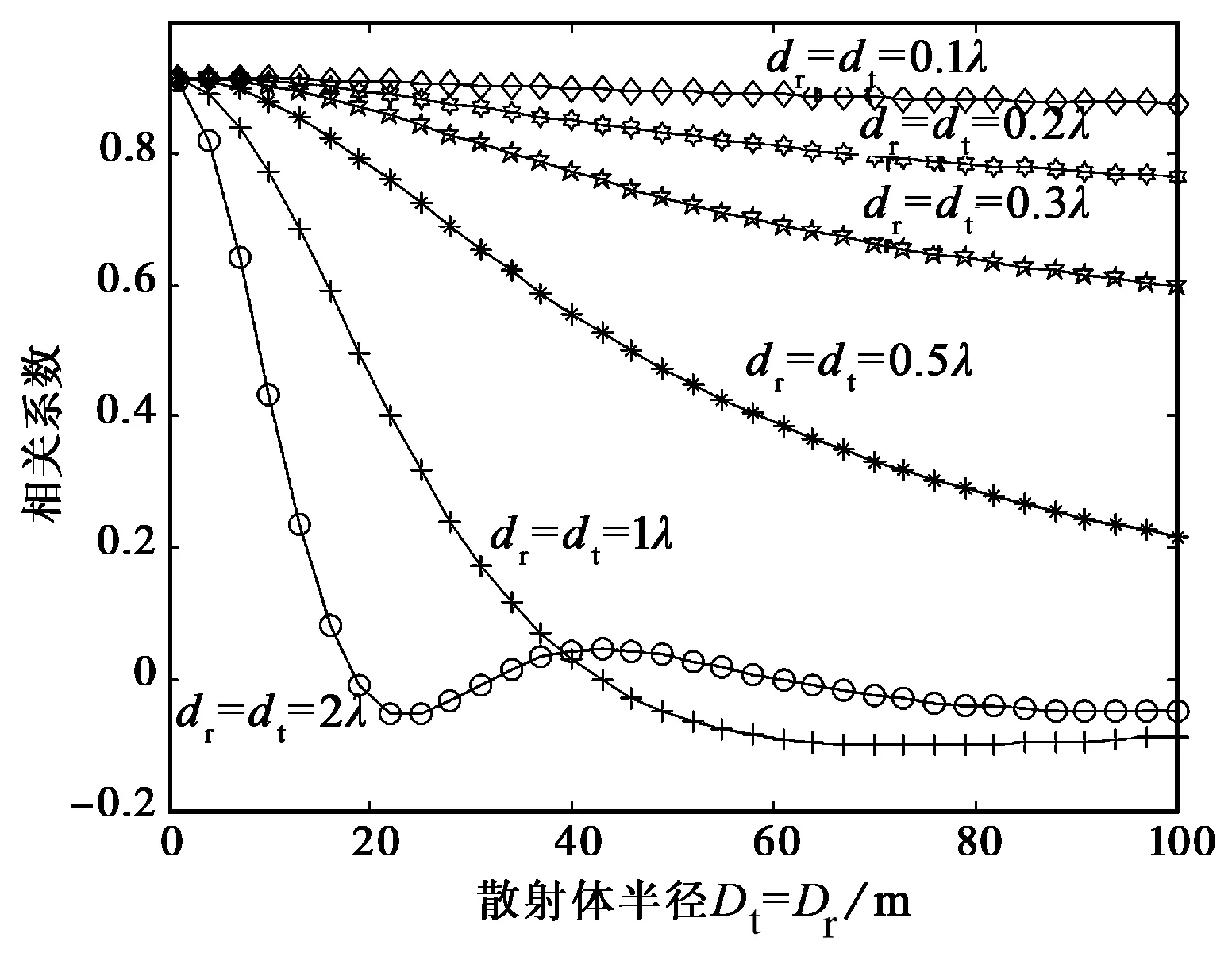
图4 波达方向为高斯分布时相关系数

在收发两端都存在散射体的情况下，由文献[7]可知信道传输系数矩阵为

(12)

式中：Rαr,dr、RαS,2Dr/S、Rαt,dt分别为N×N、S×S、M×M维的接收天线阵、接收端散射线阵与发射端散射线阵、以及发射天线阵的相关系数矩阵；Gr和Gt分别是N×S和S×M维的瑞利衰落矩阵.

公式(12)揭示了各散射参数可能对MIMO信道传输性能的影响，尤其展示了散射体半径和天线间距对计算MIMO系统信道传输特性的重要性.

2.3 信道容量计算

根据Foshini经典MIMO信道容量公式[13]，对于M×N的MIMO系统，有

(13)

式中：IN为N×N单位阵；ρ为接收阵元平均信噪比；M为发射端天线个数；H为信道传输矩阵.

把式(12)代入到式(13)，并设定系统各位置参数如下：发射天线阵与接收天线阵之间的距离为R=10 km；散射体个数S=21；发射端天线阵与接收端天线阵到散射体之间的距离为Rt=Rr=50 m；发射天线和接收天线个数同为4，即M=N=4；信噪比ρ=20 dB；发射端天线间距和接收端天线间距为dt=dr=0.5λ. 由于信道容量是一个随机变量，迭代10 000次，可得到双散射体环境下MIMO系统信道容量的仿真结果如图5所示.

图5 散射体半径对信道容量的影响

由上述仿真结果可知，在散射体数目固定、发射端散射体半径与接收端散射体半径相同的前提下，MIMO系统容量与散射体半径有密切的联系. 在散射体半径变大的情况下，系统容量随散射体半径的增大而变大，这是由于阵元间相关系数随散射体半径增大而下降导致的.

3 互耦效应对MIMO系统容量影响

由式(9)可以得出相邻阵元m、k在不计互耦效应时接收信号之间的相关系数，而由式(5)进一步可得在计及互耦效应下的接收阵列相关系数矩阵[11]为

式中：Rαr,dr是不计互耦时接收矢量的相关系数矩阵；Cr为接收端互耦系数矩阵. 根据MIMO信道Kronecker分解模型[14]及类似推导过程，可以推出存在互耦效应下发射阵列相关系数矩阵为

(15)

式中Ct为发射端阵列互耦矩阵.

所以在考虑互耦效应后，原不考虑耦合效应的信道传输系数矩阵可拓展为

在发射端天线单元功率平均分配时，考虑互耦效应的MIMO多天线系统信道容量计算公式为

(17)

假设MIMO系统采用4根发射天线和4根接收天线，则互耦网络传输矩阵依阵元间对称特性可写为

(18)

式中参数a、b、c、d可由式(1)～(4)计算得出.

由式(9)、式(15)～(18)可以计算出天线来波方向服从均匀分布时，四元线阵MIMO系统在计及和不计互耦效应时的“信道容量-累积分布函数”的关系变换图，如图6所示.

由图6可以看出：在双散射环境下，互耦效应的存在会降低MIMO多天线系统的信道容量；尤其随着天线阵元间距的缩短，互耦效应对信道容量的影响愈发明显. 以阵元间隔0.2λ为例，互耦效应使信道容量下降约16%.

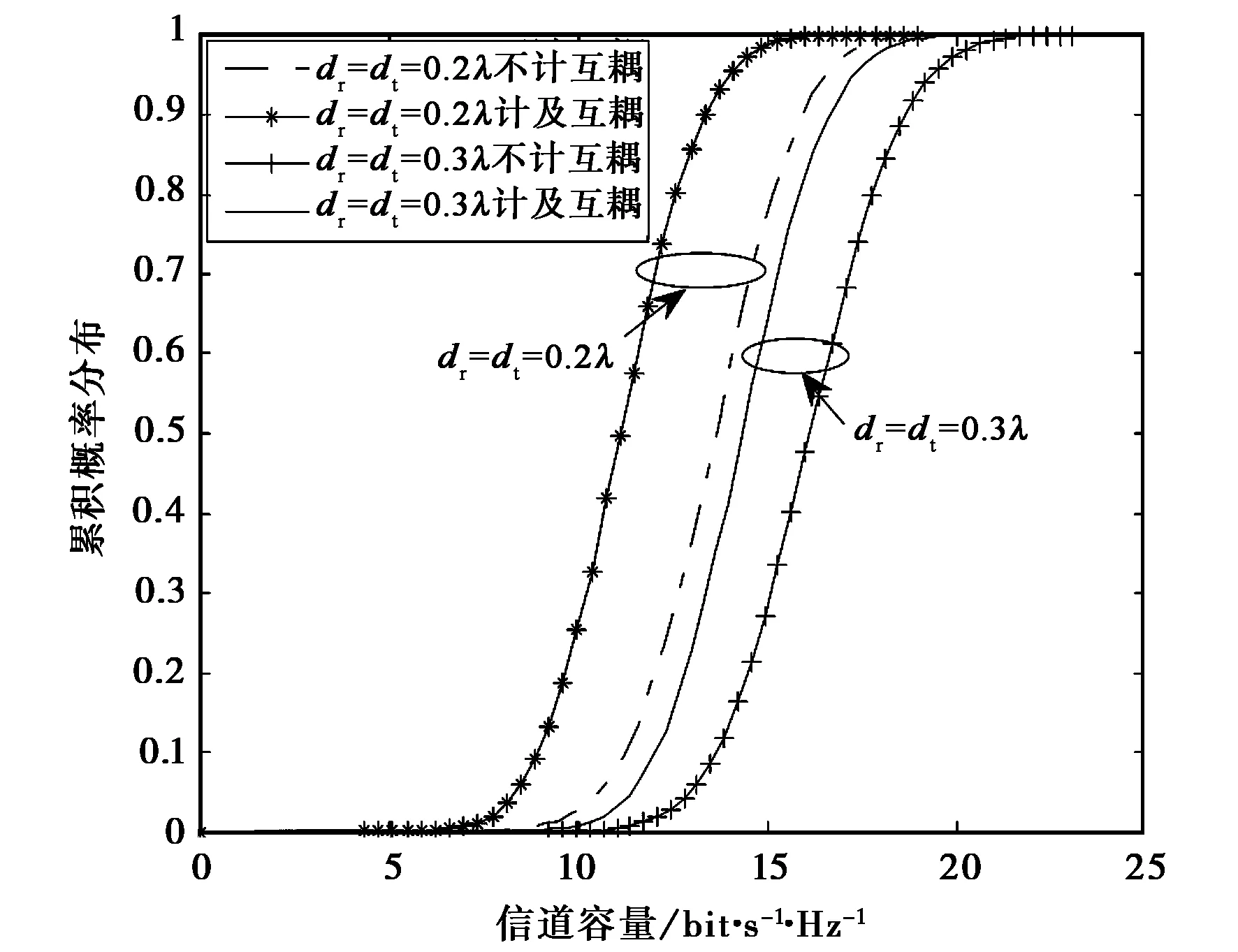
图6 均匀分布下MIMO信道容量累计概率分布曲线

当天线来波方向服从均匀分布时，MIMO系统在计及互耦和不计互耦时，信道容量随散射体半径增大而变化的曲线图如图7所示.

由图7可以看出：在双散射体环境下，当来波角谱满足均匀分布时，不论是不计互耦还是计及互耦，信道容量都随着散射体半径的增大而增大. 但结合图3相关系数仿真曲线可明显看出：当阵元间距很小时，比如0.1λ，阵列相关性明显增大，此时计及互耦后MIMO信道容量将比不计互耦时明显要小；随着阵元间距的不断增大，互耦效应亦随之减弱，此时计及互耦和不计互耦下的MIMO信道容量曲线逐渐趋于重合.

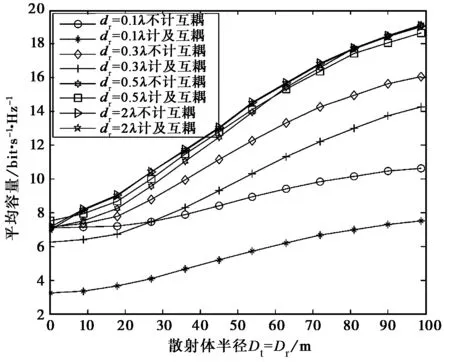
图7 均匀分布下MIMO信道容量

当来波方向服从高斯分布时，计及与不计互耦效应时系统信道容量随阵元间距和散射体半径变化的仿真曲线图如图8所示.

图8 高斯分布下MIMO信道容量

由图8可以看出，波达方向为高斯分布的MIMO系统容量随散射体半径或天线间距变化的曲线和均匀分布的情形基本类似. 只不过与图7相比，均匀分布下信道容量增加的速度更快，也就是波达方向为均匀分布的天线对散射体半径和天线间距的变化更为敏感. 同时，波达方向为高斯分布的平均容量大于波达角是均匀分布的平均容量.

图9同样显示了计及互耦和不计互耦情况下，当接收天线分别为0.2λ和0.3λ时，入射波到达方向角服从高斯分布时，MIMO系统“信道容量-累积分布函数”曲线图.

图9 高斯分布下MIMO信道容量累计概率分布曲线

由图9可知：天线间距增加时，波达方向角为高斯分布的相关瑞利衰落信道的平均容量小幅增加；同时，互耦效应也会降低MIMO信道容量. 不过与图6相比可以明显看出：随着天线间距的增大，波达方向角为均匀分布的平均容量增加速度要比高斯分布的更快，也就是波达方向角为均匀分布的天线系统对天线间距的变化更敏感.

当天线间距为0.2λ时，从图10两种分布的比较仿真可以进一步看出，在天线间距较小时，互耦效应对于均匀分布的影响要大于对于高斯分布的影响. 因此，波达方向为高斯分布时的MIMO通信系统的稳定性和可靠性要比均匀分布好.

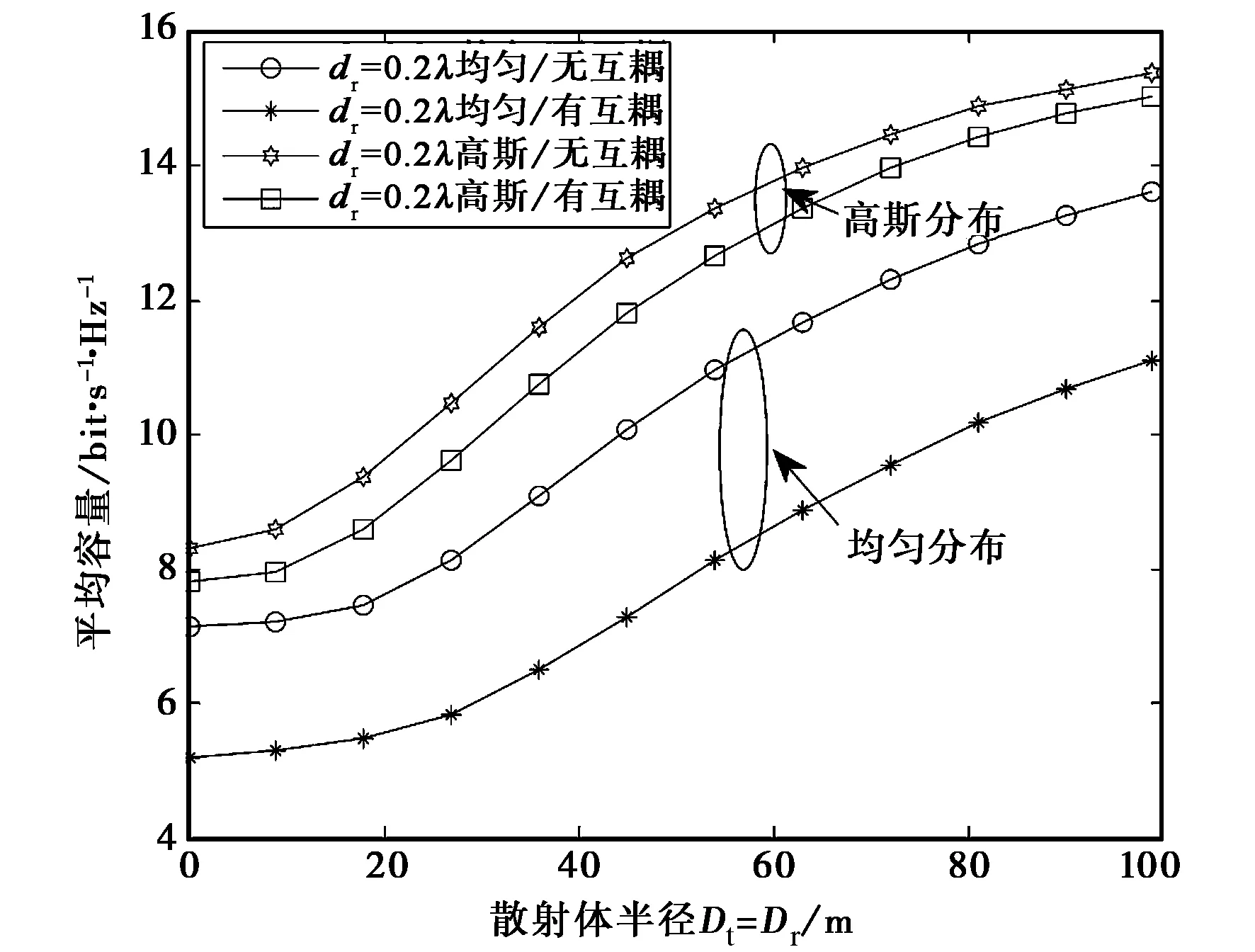
图10 天线间距较小时均匀和高斯分布信道容量比较

4 结 论

论文主要研究了收发两端存在双散射体这一较符合实际信道传输情形下，紧凑型MIMO系统中阵元互耦效应对MIMO信号空域相关及信道容量的影响. 研究结果表明，双散射信道中阵列信号的空域相关性与散射体半径之间有密切的联系，增大散射体半径可以明显地降低阵列空域相关性、提升系统容量；此外，在小尺寸天线间距(0.1～0.5λ)下引入阵元耦合效应时，不论散射体半径如何变化基本上耦合效应都将降低系统信道容量. 另外，当波达方向为高斯分布时，MIMO系统的容量稳定性要优于波达方向为均匀分布时的MIMO系统.

[1] SHUI D S, FOSCHINI G J, GANS M J, et al. Fading correlation and its effect on the capacity of multielement antenna systems[J]. IEEE Trans on Communications, 2000, 48(3): 502-513.

[2]WU Y, BERGMANS J W M, ATTALLAH S. Effects of antenna correlation and mutual coupling on the carrier frequency offset estimation in MIMO systems[C]∥ Wireless Commu Networking and Mobile Computing. Chengdu, September 23-25, 2010: 1-4.

[3] LUI H S, HUI H T, LEONG M S. A note on the mutual-coupling problems in transmitting and receiving antenna arrays[J]. IEEE Antennas and Propagation Mag, 2009, 51(5): 171-176.

[4] WALDSCHMIDT C, HAGEN J V, WIESBECK W. Influence and modeling of mutual coupling in MIMO and diversity systems[C]∥ Proc IEEE Antennas and Prop Soci Inte Symp. San Antonio, June 16-21, 2002.

[5] FLETCHER P N, DEAN M, NIX A R. Mutual coupling in multi-element array antennas and its influence on MIMO channel capacity[J]. Electronics Letters, 2003, 39(4): 342-344.

[6] ABDI A, KAVEH M. A space-time correlation model for multi-element antenna systems in mobile fading channels[J]. IEEE Journal of Selected Areas in Comm, 2002, 20(3): 550-560.

[7] GESBERT D, BOLCSKEI H, GORE D A, et al. Outdoor MIMO wireless channels: models and performance prediction[J]. IEEE Trans on Communications, 2002, 50(12): 1926-1934.

[8] 肖海林, 聂在平, 杨仕文. 室内MIMO无线信道：模型和性能预测[J]. 电波科学学报, 2007, 27(3): 385-389.

XIAO Hailin, NIE Zaiping, YANG Shiwen. Indoor MIMO wireless channels: models and performance prediction[J]. Chinese Journal of Radio Science, 2007, 27(3): 385-389. (in Chinese)

[9] 肖海林,欧阳缮, 聂在平, 等. 天线互耦对室内MIMO无线信道容量的影响[J].电子科技大学学报,2009, 38(4): 493-495.

XIAO Hailin, OUYANG Shan, NIE Zaiping, et al. Effect of mutual coupling on the capacity of indoor MIMO wireless cannels[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(4): 493-495. (in Chinese)

[10] 李 忻, 聂在平. 天线互耦对MIMO无线信道性能的影响[J]. 电波科学学报, 2005, 20(4): 546-551.

LI Xin, NIE Zaiping. Effect of mutual coupling on the performance of MIMO wireless channels[J]. Chinese Journal of Radio Science, 2005, 20(4): 546-551. (in Chinese)

[11] 李岳衡, 赵 静. 互耦效应对四元方阵天线阵列信道容量的影响[J].电波科学学报, 2011, 26(1): 145-150.

LI Yueheng, ZHAO Jing. Effect of mutual coupling on the capacity of 4-element squared antenna array MIMO systems[J]. Chinese Journal of Radio Science, 2011, 26(1): 145-150. (in Chinese)

[12] 李英梅, 邵玉斌, 王 纯. 不同天线相关分布特性下的MIMO容量性能分析[J].云南民族大学学报, 2007, 16(3): 277-280.

LI Yingmei, SHAO Yubin, WANG Chun. Performance of the MIMO capacity with the different antenna distribution characteristic[J]. Journal of Yunnan Nationalities University, 2007, 16(3): 277-280. (in Chinese)

[13] FOSCHINI G J, GANS M J. On limits of wireless communication in a fading environment when using multiple antennas[J]. Wireless Personal Communications, 1998, 6(3): 311-335.

[14] YU K, BENGTSSON M, OTTERSTEN B, et al. Modeling of wideband MIMO radio channels based on NLOS indoor measurements[J]. IEEE Trans on Vehicular Tech, 2004, 53(3): 655-665.