基于Excel环境下概率案例的分析

罗幼芝

(长沙民政职业技术学院，湖南长沙 410004)

1999年，教育部提出了高职高专数学课程“以应用为目的，以够用为度”的原则。在这一背景下，高职数学课程的教学应当把数学概念和专业实际联系起来，学生不再是机械地学习纯粹的数学理论知识，而要把这些数学知识和专业实际中遇到的典型问题结合起来，在解决这些问题时不再只是利用传统方式解决，还可以借助相关工具如Excel加以解决。这样能让我们真切感受到它的实用性，有利于提高学生学习数学的兴趣，让学生学习数学有更强的目的性。下面笔者就概率中的相关问题来阐述这一过程。

一、彩票中奖概率

1. 典型案例

某地发行福利彩票，每张彩票的号码是7个数字的无序数组，开奖时，用一个摇奖机，里面装有分别写上01,02,…，35的35个小球。充分搅拌这些小球一分钟，从出口处掉出一个小球，记下小球上的数字。摇出的小球不放回摇奖机中，重复刚才的做法，一直到产生一个7个数字的无序数组，记作a，设有一、二、三等奖。规定：彩票号码与a完全一样时，得一等奖；彩票号码与a有6个数字一样时，得二等奖；有5个数字一样时，得三等奖。

试问：买一张彩票，中一、二、三等奖的概率各是多少?

2. 解决方案

根据题意，将问题转化为一个袋子中有35个彩球，其中红球7个，白球28个，每次随机的取出一只，第一次取到的球不放回袋中，第二次从剩余的球中再取一球，共取7次，求取到7球中全是红球、有6个红球和有5个红球的概率。经过转换，问题变为无放回的随机抽样(超几何分布)，根据其概率分布即可计算出相应的概率值。

3. 解决办法

利用Excel中的超几何分布函数(HYPGEOMDIST函数)可计算出相应参数下超几何分布的概率。

4. 使用Excel的求解步骤

第一步：新建一个工作表，输入表头“应用超几何分布函数HYPGEOMDIST求概率”。

第二步：分别单击C2、E2、C3和E3单元格，输入已知参数:N=35， M=7，n=7，x=7。

第三步：运用HYPGEOMDIST求7个球中全为红球的概率，在B5单元格输入“=HYPGEOMDIST(E3，C3，E2，C2)”，结果如图11-1所示。

图11-1应用超几何分布求概率

利用相同的原理可求得x=6及x=5的概率值。

在熟悉超几何分布函数的基础上，可以绘制超几何分布的概率分布图。继续上述问题，可以求得各种情形下的中奖概率。具体操作如下：

第一步：新建Excel工作表，输入 “超几何分布函数概率分布图”。

第二步：分别单击C2、E2和C3单元格，输入己知参数N=35， M=7，n=7。

第三步：设定样本中中奖的号码个数x序列。在B6—B13单元格输入x为0，1，…，7的取值。

第四步：求不同的x对应的概率。单击C6单元格，输入"= HYPGEOMDIST(B6，$C$3,$E$2，$C$2)”，再次单击C6单元格，将鼠标至于C6单元格右下角，当光标变为小黑十字时拖曳至C13单元格，求出其他x对应的概率值，如图11-2所示。

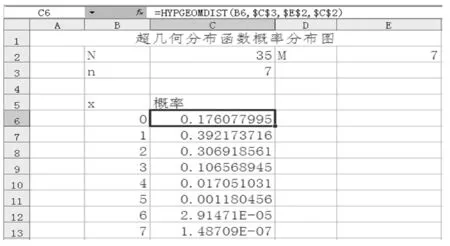
图11-2超几何分布概率分布图

二、保险赔付概率

1. 典型案例

某保险公司在一天内承保了5000张相同年龄，为期一年的寿险保单，每人一份。在合同有效期内若投保人死亡，则公司需赔付3万元。设在一年内，该年龄段的死亡率为0.0015，且各投保人是否死亡相互独立。求该公司对于这批投保人的赔付总额不超过30万元的概率。

2. 解决方案

死亡人数X服从B(5000,0.0015)的二项分布(详见本章第四节)，根据泊松定理，当n很大、p很小时，二项分布的概率值可由参数为λ=np的泊松分布的概率值近似，此案例中λ=5000×0.0015=7.5，通过泊松分布(详见本章第四节)的概率分布函数可求得相应的概率值。

3. 解决办法

利用Excel中的泊松分布函数(POISSON函数)可计算出相应参数下的概率。

4. 使用Excel的求解步骤

第一步：新建Excel工作表，输入表头“应用泊松分布函数POISSON求概率值”。

第二步：分别单击C2、E2单元格，输入己知参数λ=7.5,x=10。

第三步：求该公司对于这批投保人的赔付总额等于30万元的概率(即死亡人数为10个)，单击C4单元格，输入“=POISSON(E2,C2,0)”。

第四步：求该公司对于这批投保人的赔付总额小于30万元的概率。单击C4单元格，输入“=POISSON(E2,C2,1)”，结果如图11-3所示。

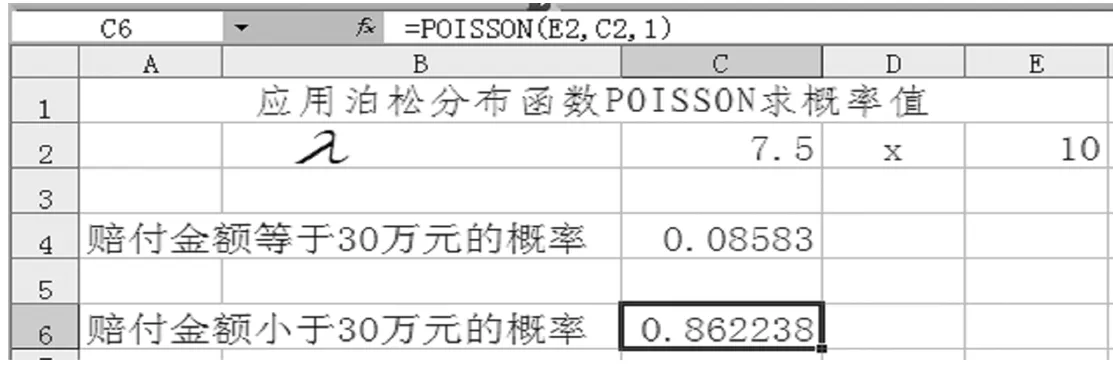
图11-3应用POISSON分布函数求概率值

为了更好地理解泊松分布，下面说明如何绘制泊松分布的概率分布图和概率分布函数图。继续保险赔付概率问题，计算赔付金额为0-45万元间不同金额下的概率，步骤如下：

第一步：新建Excel工作表，输入表头“泊松分布的概率分布图”。

第二步：单击C2单元格，输入已知参数λ=7.5。

第三步：采用序列填充生成“赔付金额”及“死亡人数”序列，由于保单有5000张，此处选定求x取值为0,1，…，15，即赔付金额取值为0，3，…，45的概率，死亡人数为15人以上的概率仍然存在，但极小。

第四步：运用POISSON函数求出不同赔付金额对应的概率，单击C4单元格，输入“=POISSON(B4，$C$2，0)”，再次单击C4单元格，拖曳至C19单元格，求出其他死亡人数对应的概率值；单击D4单元格，输入“=POISSON(B4，$C$2，1)”，再次单击D4单元格，拖曳至C19单元格，求出其他次数对应的累计概率值，结果如图11-4所示。

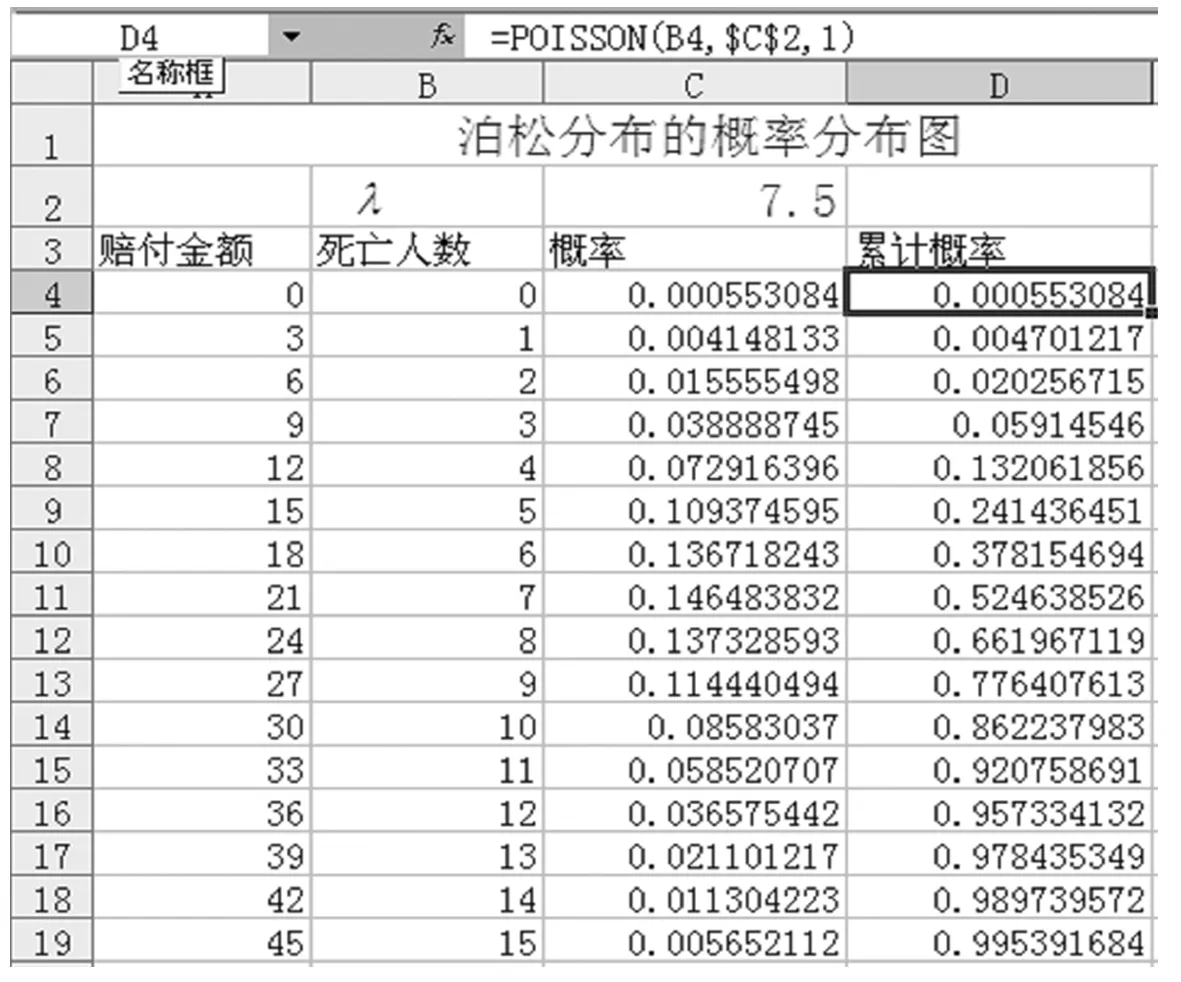
图11-4POISSON分布概率分布图

根据上图中所给的不同赔付金额下的累积概率值，保险公司可估算出应向投保人收取多少保费。

结语

通过以上案例的学习，让我们更加明确高职数学教育必须面向工作实际，解决实际问题，真正做到学校的教育是以培养生产、建设、服务和管理第一线的高端技能型专门人才为主要任务。

参考文献：

[1]李朋．Excel统计分析实例精讲[M]．北京：科学出版社，2006.

[2]陈士成．实用管理运筹学——基于Excel[M]．北京：清华大学出版社，2011.

[3]余小飞．面向专业需求的高职数学教学改革研究[J]．漯河职业技术学院学报，2011，(2).