累积辐照影响静态随机存储器单粒子翻转敏感性的仿真研究

丁李利 郭红霞 陈伟 闫逸华2) 肖尧 范如玉2)

1)(西北核技术研究所，西安 710024)

2)(清华大学工程物理系，北京 100084)

(2013年5月2日收到;2013年6月4日收到修改稿)

1 引言

空间辐射环境是由质子、电子、重离子等组成的复杂环境，星用微电子器件可能受到总剂量效应、单粒子效应和位移损伤的影响.在地面考核试验中，一般假设不同类型的辐射效应是相互独立的[1,2]，也有大量相关报道研究了不同效应间发生协同影响的可能性.早在1983年，Knudson等[3]首先研究了累积剂量对于动态随机存取存储器(DRAM)器件单粒子翻转敏感性的影响，其测试结果表明，存储值不变的情况下，单粒子翻转截面将随着器件受辐照所累积剂量的增加而减小.令人疑惑的是，Cambell和Stapor[4]等在随后针对静态随机存取存储器(SRAM)器件的测试中发现，随着累积辐照剂量增加且存储值不变的情况下，三类SRAM器件的单粒子翻转截面均表现出增大的趋势.迄今为止，相关测试结论已经屡屡出现，但并没有表现出一致的规律.部分结果表明，当SRAM器件在累积辐照与重离子测试阶段保持相同的存储图形时，对应的单粒子翻转截面将增大[5-8]，甚至增大两个量级[7].另一部分结果表明，只有所存储图形全部改为相反值时，对应的单粒子翻转截面才会增大，否则就会减小[3,6,7,9].其他结果则表明，累积辐照对于某些SRAM器件的单粒子翻转截面不会出现明显的影响[6,7].

针对上述问题，Bhuva等[9]针对大尺寸四管SRAM单元给出了相应的解析分析，其中单纯考虑了累积辐照导致金属氧化物半导体(MOS)管阈值电压漂移的损伤机制.Matsukawa等[10]采用重离子微束辐照的方法，认为大尺寸SRAM单元中nMOS和pMOS管的单粒子翻转敏感性将随累积辐照剂量的增加呈现出相反的变化趋势.Schwank等[6]利用光发射谱仪对累积辐照作用后的深亚微米SRAM器件开展损伤分析，判定内部的电压转换电路对整个器件的功耗电流贡献最大，所以很可能是导致器件单粒子翻转敏感性发生变化的直接原因.综合来看，目前的相关研究以整芯片实测为主，与此相关的解析分析和微束辐照等针对的都是大尺寸器件.当器件进入深亚微米尺度以后，累积辐照对MOS管的影响机制已经发生了显著变化，有必要对相关的解释加以修正.

本文采用仿真手段研究累积辐照对于SRAM器件单粒子翻转敏感性的影响.首先结合已有的0.18µm单管实测数据，对三维器件仿真模型的结构、掺杂及辐射相关参数进行校准;同时采用解析分析的方法，比较累积辐照对于大尺寸(特征尺寸为微米量级)和深亚微米尺度(特征尺寸≤0.25µm)下SRAM单元单粒子翻转敏感性的影响差异;接下来利用校准后的器件模型计算不同累积剂量下单个nMOS管输出单粒子瞬态脉冲的变化;最后，利用混合模拟详细计算了六管SRAM单元中对应不同累积剂量情况下，离子分别入射四个中心单管时的电学响应变化.

2 三维仿真模型介绍

为提高TCAD(technology computer-aided design)模拟的可信度，首先利用反向建模方式对三维器件模型的结构及掺杂参数进行校准.本文中结合0.18µm工艺对应的单管试验片，首先利用精密半导体参数测试仪HP4156A获取常态情况下的电学特性曲线，将半导体数值模拟软件ISE TCAD得到的仿真结果与实测曲线进行反复对比，最终得到了符合较好的三维器件模型.图1给出了宽长比为W/L=0.22/0.18µm nMOS管所对应的校准结果.

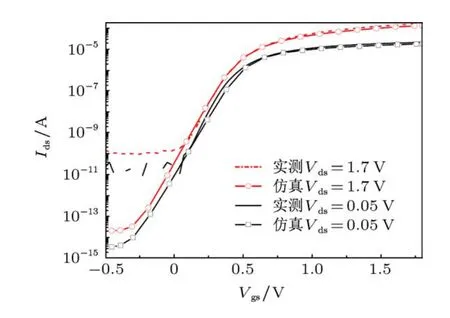
图1 nMOS管Ids-Vgs曲线的校准结果，W/L=0.22/0.18µm

模拟总剂量效应对器件的影响时，需要考虑辐射在氧化物材料中沉积能量产生过剩载流子、过剩载流子在氧化物中的输运、陷阱俘获空穴产生陷阱电荷、电子与陷阱电荷中的空穴发生复合等一系列过程.计算过程中涉及的待定参数包括：氧化层中的中性空穴陷阱浓度Nt，空穴被中性陷阱俘获的作用截面σp和被陷阱俘获的空穴与电子发生复合反应的截面σr，这就需要对辐射效应相关的参数进行校准.计算过程中所需的三维器件结构如图2所示，其中重点展示出场氧隔离区(shallow trench isolation，STI)，该部分区域内定义氧化物材料为宽禁带半导体.

利用西北核技术研究所的60Co源针对单管试验片开展总剂量效应实验，剂量率选取为50 rad(Si)/s，辐照过程中单管的栅极接1.8 V，测试得到累积剂量为58，100，140和200 krad(Si)情况下单管试验片的电学特性曲线.

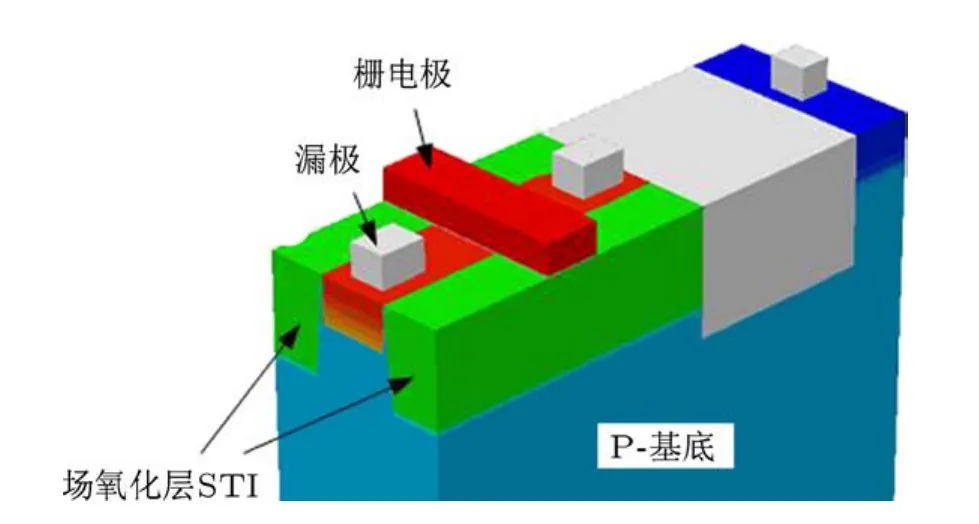
图2 计算单管总剂量效应时的器件模型示意图

器件尺寸减小至深亚微米尺度后，辐照过程仍会显著改变nMOS的电学特性，但对pMOS的影响会变得非常小.对于本文中的0.18µm工艺，其中尺寸为0.22/0.18µm的pMOS管在辐照剂量累积至200 krad(Si)时，对应的阈值电压漂移将小于-10 mV，并且未伴随出现截止区漏电流增大的附加现象.

最终的校准结果显示，当空穴陷阱均匀分布于 STI隔离区范围内，峰值浓度Nt=3×1017cm-3，陷阱俘获空穴的截面值为5×10-12cm2，电子与陷阱发生作用使空穴被释放并复合的截面值为1×10-14cm2时，模拟结果与测试结果之间的一致性较好.图3给出了分别利用TCAD模拟计算和辐照试验获取的关态漏电流(Vgs=0 V，Vds=0.05 V)随累积剂量的变化关系，对应单管尺寸为W/L=0.22/0.18µm.

确定了这些参数的具体数值后，就可以定量计算辐照前后器件的宏观电学响应及载流子微观输运过程.SiO2材料对应的过剩载流子产生率g0=7.6×1012rad-1·cm-3，而空穴产额Y(逃脱复合的空穴数/辐射诱发的空穴数)的关系表达式为[11]

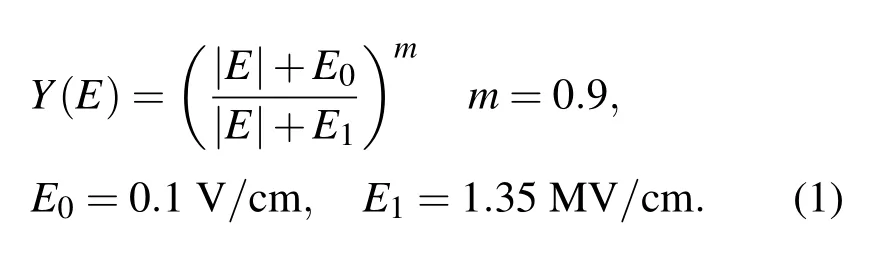
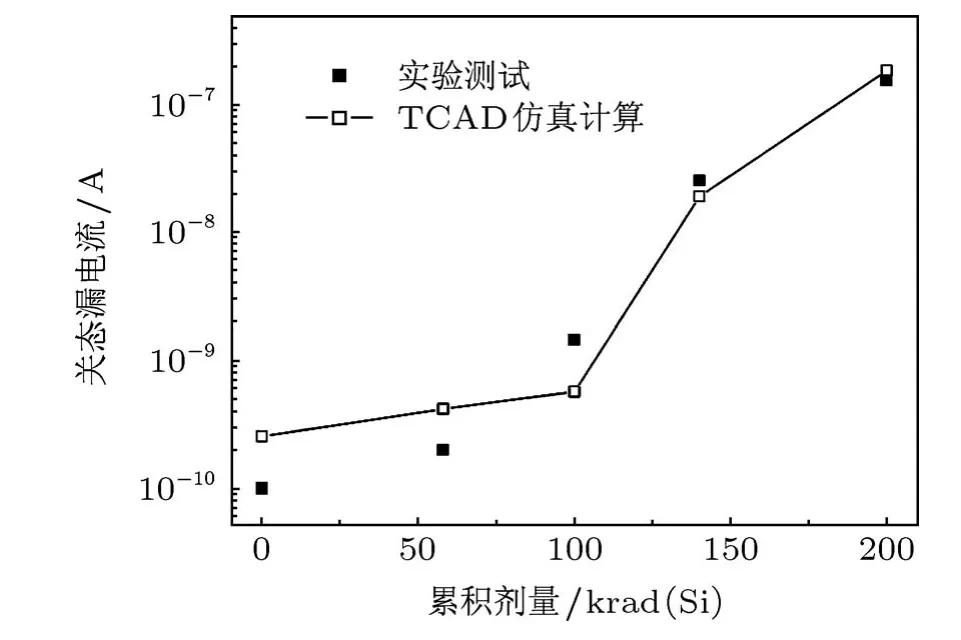
图3 nMOS管不同累积剂量下关态漏电流(Vgs=0 V，Vds=0.05 V)的校准结果，W/L=0.22/0.18µm

3 累积辐照影响不同尺寸SRAM单元单粒子翻转敏感性的解析分析

SRAM器件中的最主要组成为SRAM单元，其常见结构分为四管和六管两种.图4为典型六管SRAM单元的结构示意图，其主体部分为两个对接的反相器，分别由P1，N1和P2，N2组成.四管SRAM单元中，图4所示的P1和P2将由阻值较大的电阻所代替.

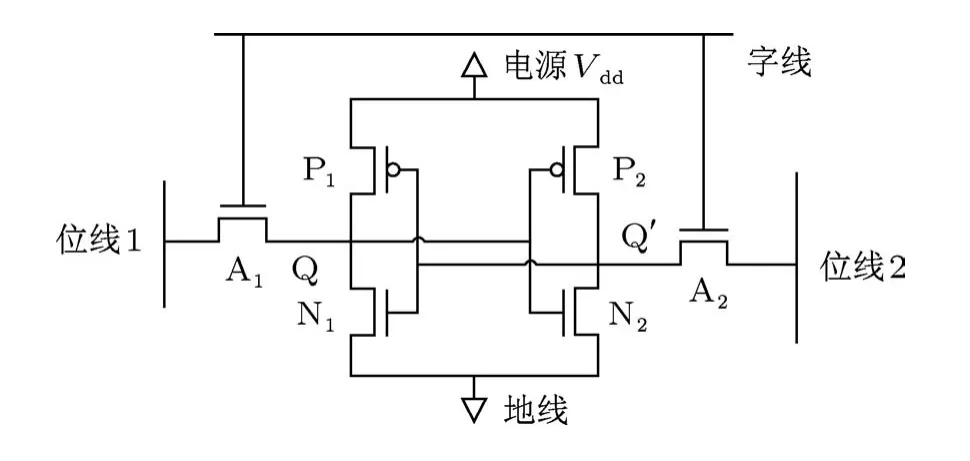
图4 典型六管SRAM单元的结构示意图

分析SRAM单元的稳定性及工作原理时，常采用如图5所示的曲线组，下面将结合图4与图5进行分析.令六管SRAM单元中的存储点Q′连接Vin，则存储点Q连接Vout.六管SRAM单元中左端反相器对应的输入电压为Vin，输出电压为Vout，其电学特性可表征为图5中的转移特性曲线1.与此相对应的是，右端反相器对应的输入电压为Vout，输出电压为Vin，其电学特性可表征为图5中的转移特性曲线2.

接下来说明转移特性曲线所代表的含义：以图4中左端反相器所代表的转移特性曲线1为例，当Vin=0 V时，晶体管P1处于开启状态，N1处于关断状态，所以Vout=Vdd，该区域在图5中表征为S1;随着Vin的持续增加，当满足高于N1阈值电压VN1,th并低于Vdd+VP1,th时，其中VP1,th代表P1管阈值电压，同时受到N1和P1管的分压作用，Vout的数值将介于0 V和Vdd之间，该区域在图5中表征为S2;当Vin高于Vdd+VP1,th以后，P1管彻底关断，只有N1管保持开启状态，所以Vout=0 V，于是进入S3区域.三个区域对应的输入电压范围分别为：VS1=VN1,th，VS2=Vdd+VP1,th-VN1,th，VS3=-VP1,th.令转变点电压Vsw1代表两条转移特性曲线的中心交点在特性曲线1输入电压轴上的投影，即所存储电压从高电平跳变为低电平的临界电压.

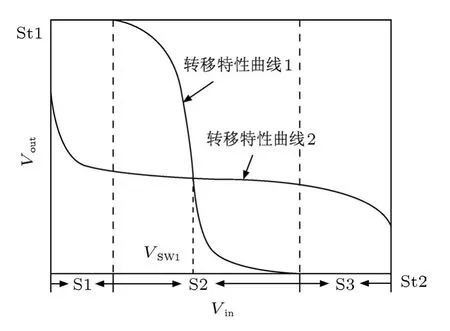
图5 SRAM单元中两个对接反相器的转移特性曲线

图5中，两条转移特性曲线相交于St1和St2点时，曲线斜率近似为零，说明对接反相器将处于稳定工作状态.当SRAM单元处于St2工作状态时(Q连接低电平)，对单粒子效应敏感的区域包括N2管和P1管的漏极，发生状态翻转所需的临界电荷分别为

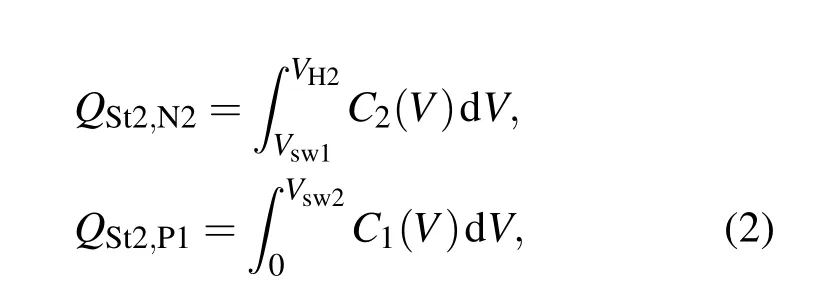
其中，C1(V)代表晶体管N1，P1的栅极与耗尽层对地的电容值，C2(V)代表晶体管N2，P2的栅极与耗尽层对地的电容值，Vsw1和Vsw2分别代表转移特性曲线1，2的电压转换点，VH2代表转移特性曲线2的输出电平最高值.

当SRAM单元处于St1工作状态时(Q连接高电平)，对单粒子效应敏感的区域包括N1管漏极和P2管漏极，发生状态翻转所需的临界电荷分别为

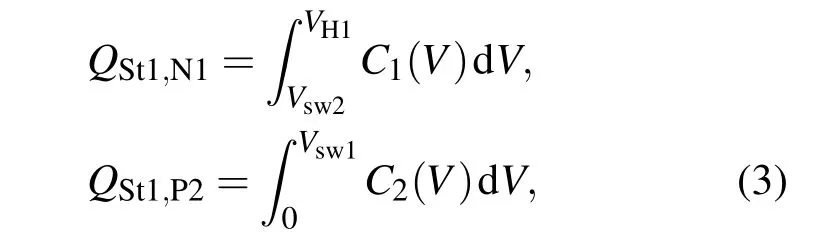
其中VH1代表转移特性曲线1的输出电平最高值.

对于大尺寸器件(特征尺寸为微米量级)，总剂量效应对于MOS单管的影响主要体现为阈值电压明显减小.假设辐照过程中Q连接高电平(St1工作点)，则受损伤的单管主要为N2和P1，导致VN2,th和VP1,th减小.于是，转移特性曲线2的S1区域将变窄，导致Vsw2随之减小;相应的两条转移特性曲线的交点将向左上方移动，导致Vsw1随之增大.结合(2)式可知，状态St2中N2与P1对应的临界电荷值均减小;结合(3)式可知，状态St1中N1和P2对应的临界电荷值均增大.换言之，六管SRAM单元在前期累积辐照阶段与后期单粒子作用阶段处于相反的工作状态时，对应的单粒子翻转敏感性将增大，反之则会减小.对于大尺寸四管SRAM单元，忽略了P1与P2管受累积剂量辐照后的阈值电压漂移，所得结论如下：前期累积辐照阶段与后期单粒子作用阶段处于相反的工作状态时，单元的单粒子翻转敏感性将增大，反而则无影响.

当器件尺寸减小进入深亚微米尺度(特征尺寸≤0.25µm)，总剂量效应对于nMOS单管的影响主要体现为关态漏电流明显增大，阈值电压的漂移反而可以忽略不计，同时可以忽略对于pMOS单管的影响.若辐照过程中Q连接高电平(St1工作点)，则N2的关态漏电流明显增大，导致转移特性曲线2的高电平值VH2降低，电压转换点Vsw2减小.结合(2)和(3)式可以得到，QSt2,N2将减小(高电平值减小所致)，而QSt1,N1将明显增大.所以，对于特征尺寸较小的SRAM单元，只有当前期累积辐照与后期单粒子作用阶段处于相反的工作状态，单元的单粒子翻转敏感性才会表征出增加的趋势.

4 累积辐照对单粒子瞬态脉冲的影响

为研究累积辐照对于SRAM器件单粒子翻转效应的作用机制，首先要了解累积辐照对于单粒子脉冲形状的影响.需要注意的是，总剂量效应的最劣偏置是nMOS管栅极连接高电平，而瞬时单粒子效应的最劣偏置是pn结处于反偏状态，且在nMOS管截止区的效应最为明显.综合来说，研究累积辐照对于nMOS管单粒子瞬态脉冲影响的最劣偏置为：在前期剂量累积阶段栅极电压Vg=1.8 V，其他电极电压Vd=Vs=Vb=0 V，到达设定的累积剂量后，改变偏置情况为漏极电压Vd=1.8 V，其他电极电压Vg=Vs=Vb=0 V.

表征重离子入射时，设定器件材料中产生过剩载流子的空间分布与时间分布均服从Gauss分布，特征半径选取为0.1µm，特征时间选取为2 ps，产生过剩载流子的峰值时刻为20 ps[2].设定重离子沿nMOS管漏极中心垂直入射，LET=2 MeV·cm2·mg-1.图6给出了不同累积剂量下由单粒子入射所引发的电流脉冲波形，可以看出：随着累积剂量的增加，单粒子所引发电流脉冲的峰值并没有呈现出明显的变化，不同曲线间最主要的差异体现在电流初始值，对应着单粒子入射前漏极电压Vd=1.8 V，其他电极电压Vg=Vs=Vb=0 V所对应的漏极电流，这是由累积剂量增加后nMOS管关态漏电流的增加所决定的.

图6 不同累积剂量下nMOS管单粒子脉冲形状的差异，LET=2 MeV·cm2·mg-1

可以看出，累积辐照对于nMOS管的单粒子瞬态脉冲形状确实会产生可见的影响，但对于稍大规模电路单元的定量影响仍然需要进一步评估.

5 仿真计算

利用前期校准得到的0.18µm器件模型，对六管SRAM单元执行混合模拟，定量计算不同累积剂量及不同存储图形情况下，累积剂量增加对于单元单粒子翻转敏感性的影响规律.图7所示为混合模拟的示意图，SRAM单元的中心单管 N1与 N2(W/L=0.22/0.18µm)，P1与 P2(W/L=0.35/0.18µm)利用三维器件模型进行构造并联立求解泊松方程与电子、空穴连续性方程，其他如A1，A2及不同单管间的连接关系则利用电路模型进行构造并求解电路节点的电流与电压平衡方程.

当累积辐照过程中固定Q连接低电平(St2工作点)时，受总剂量效应影响最严重的单管将为N1管.后期单粒子效应作用阶段，如果Q仍然连接低电平(即不改变偏置状况)，则对单粒子敏感的区域为N2和P1管的漏极;反之，如果Q连接高电平，则对单粒子敏感的区域为N1和P2管的漏极.总体来说，可以归纳为如表1所示的四种情况.

如表1所示，随着累积剂量的增加，六管SRAM单元的单粒子翻转敏感性将发生明显的变化.其中，No.1与No.3两种情况下(累积辐照与单粒子作用阶段存储值相同)，SRAM单元的单粒子翻转敏感性将随着剂量值的增高而减小.而对于No.2和No.4两种情况(累积辐照与单粒子作用阶段存储值相反)，单元的单粒子翻转敏感性将随之增大.

No.1情况下，SRAM单元在前期累积辐照与后期单粒子作用阶段处于相同的工作状态，重离子入射相对来说受总剂量影响很小的N2管漏极中心.图8给出了单粒子作用阶段SRAM单元所存储电平值随时间的变化，时间尺度为1 ns，LET=1.11 MeV·cm2·mg-1.

图7 六管SRAM单元执行混合模拟的示意图

表1 利用仿真手段计算累积剂量与单粒子效应共同作用的分类描述及初步结果

从图8中可以看出，当累积剂量为零时(辐照前)，单粒子入射带来的扰动将导致SRAM单元发生状态翻转，Q节点将从低电平改变为高电平.随着累积剂量的增加，这种情况逐渐发生了改变.当累积剂量为140，200和300 krad(Si)时，同样LET值的重离子入射将不能导致状态发生翻转，而只是出现一个瞬时的变化，一定时间后还能够恢复至初始时刻的水平.需要注意的是，当累积剂量为60 krad(Si)时，单粒子扰动项对于节点存储电压的影响趋近于临界状态，电压值出现瞬时变化后将持续很长一段时间稳定下来，从图中的趋势中可以看出，该情况下SRAM单元最终仍然会发生状态翻转.

图8中标出了70.7 ps时刻点，可以看出，在t≤70.7 ps时，不同累积剂量所对应的电平变化曲线基本重合，当t＞70.7 ps时，不同曲线间出现了明显的偏离.为了分析累积剂量影响SRAM单元单粒子翻转敏感性的原因，考虑到N1是整个SRAM单元中受累积辐照影响后惟一发生明显性能退化的单管，图9给出了70.7 ps时刻N1漏极电流随累积剂量的变化.N1所在电流通路是与单粒子效应直接作用的N2所在电流通路相对的，N2管漏极电流为重离子入射后产生过剩载流子并被节点收集而产生的电流脉冲，其幅值越高，SRAM单元发生状态翻转的可能性越高;受N2漏极电流的影响，P1和N1的栅极电压将首先出现小幅度的降低，导致Q节点电平随之增加，其增加的幅度与N1的电导值相关，即相同电压偏置情况下，N1的漏极电流越高，Q节点受扰动后电平增加的幅度将越小，于是SRAM单元发生状态翻转的可能性越低.

图8 No.1情况下，重离子入射后两个存储节点的电压值随时间的变化

从图9中可以看出，随着累积剂量的增加，t=70.7 ps时N1的漏极电流随之增加，结合上文中的分析，SRAM单元发生状态翻转的可能性将随之降低，这与图8中不同曲线的对比是相一致的.

No.2情况下，SRAM单元在前期累积辐照与后期单粒子作用阶段处于相反的工作状态，重离子入射受总剂量影响最大的N1管漏极中心.图10和给出了单粒子作用阶段SRAM单元所存储电平值随时间的变化，时间尺度为1 ns，LET=1.2 MeV·cm2·mg-1.

图9 与图8相对应，70.7 ps时刻N1漏极电流随累积剂量的变化

从图10中可以看出，当累积剂量为零时(辐照前)，重离子入射带来的扰动不足以使SRAM单元发生状态翻转，Q节点受扰动后将恢复为高电平.当累积剂量为60 krad(Si)时，Q节点受扰动后仍然能够恢复为高电平，但可以看出其扰动幅值已经有所增加.随着累积剂量的继续增加，当累积剂量为140，200和300 krad(Si)时，同样LET值的重离子入射将导致状态翻转的发生.

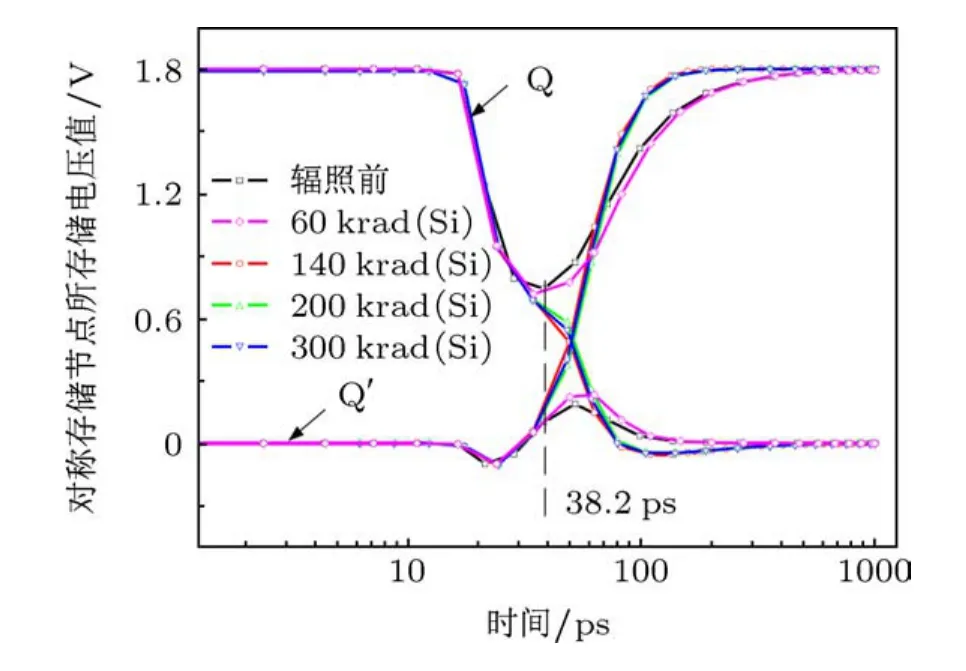
图10 No.2情况下，重离子入射后两个存储节点的电压值随时间的变化

与上文相似，图10中同样标出了类似于临界时刻的时间线，该情况下t=38.2 ps，图11给出了对应的N1漏极电流随累积剂量的变化.此时N1的漏极电流成分主要为重离子入射后产生过剩载流子并被节点收集而产生的电流脉冲，其幅值越高，SRAM单元发生状态翻转的可能性将越高.从图11中可以看出，随着累积剂量的增加，t=38.2 ps时N1的漏极电流将随之增加，于是增大了SRAM单元发生状态翻转的可能性.

No.3与No.4两种情况下，重离子分别入射P1和P2漏极，对应结论与上述两种情况是类似的：当累积剂量与单粒子入射阶段存储相同数值时，SRAM单元的单粒子翻转敏感性将减弱;存储相反值时，对应的单粒子翻转敏感性将增强.

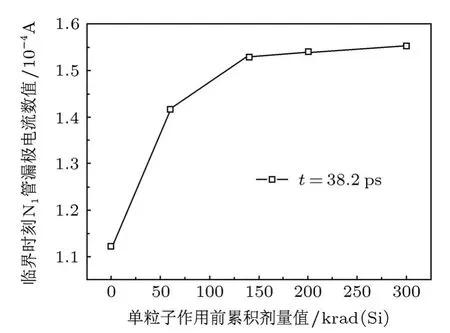
图11 与图10相对应，38.2 ps时刻N1漏极电流随累积剂量的变化

从文献中的报道可知，并不是所有SRAM器件的测试结果都符合上述结论，部分SRAM器件表征出的趋势甚至是相反的，即当累积辐照与单粒子入射阶段存储相同数值时，SRAM器件的单粒子翻转敏感性才会增强.因此，必须考虑除SRAM单元以外，器件中的其他组成部分是否同样发挥了作用.参照Schwank等[7]的相关工作，其中共考核测试了六款SRAM芯片，虽然不同芯片反映出的现象并不一致，但却在另一方面得出了一致的结论，即考察总剂量/单粒子协同影响时，最劣情况下的存储数值组合对应着SRAM器件功耗电流达到最大值的情况.例如，如果累积辐照阶段SRAM芯片存储的数值为55 H，那么若辐照后存储55 H时的功耗电流低于相反值AAH，则后期单粒子作用阶段对应翻转截面增加的存储值将为AAH;反之，若辐照后存储55 H时功耗电流更高，则后期存储55 H(即不改变存储状态)时器件的单粒子翻转敏感性将增大.

对于SRAM器件中的单元而言，令辐照前节点Q存储低电压，计算单粒子作用阶段节点Q存储不同电平时SRAM单元的功耗电流变化，如图12所示.从图中可以看出，当累积辐照与单粒子作用阶段存储相同值时，SRAM单元的功耗电流将基本上维持不变;当存储相反值时，对应功耗电流将表征出明显的增长，其增长趋势与单个nMOS管受总剂量影响后关态漏电流的变化相一致.

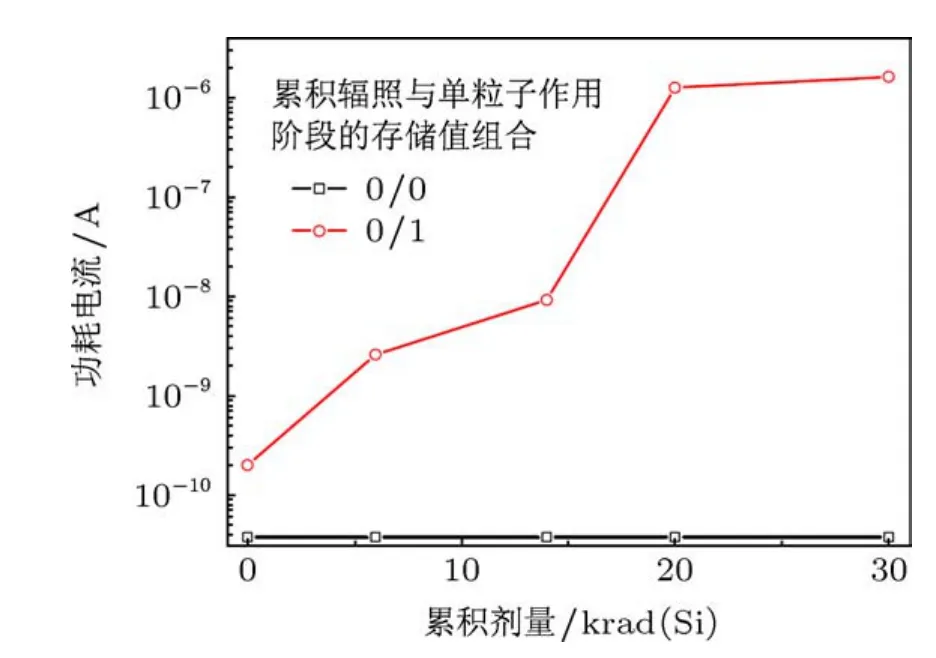
图12 累积辐照与单粒子作用阶段存储相同值与相反值时对应功耗电流随累积剂量的变化

利用解析分析就可以解释图12中的计算结果，累积辐照对nMOS单管的影响主要体现为截止区漏电流增大，其最劣表征对应着辐照过程中栅极接高电平，测试过程中栅极接低电平的情况，此时辐照前后的差异才能最大限度地体现出来.所以，导致部分SRAM器件在累积剂量与单粒子作用阶段存储相同值时功耗电流增大、存储相反值时功耗电流减小的机制必然不是由于其中的存储单元，而是与其他内部电路相关.SRAM器件的内部电路还包括灵敏放大器、译码器、IO电路、电压转换电路等，其中最可能受存储值影响的是灵敏放大器，因为其结构中同样包含对接反相器，相对而言，译码器、IO电路、电压转换电路等都属于逻辑电路，不会与存储值的图形产生直接的联系.

6 结论

本文主要利用仿真手段研究了累积辐照对于SRAM器件单粒子翻转敏感性的影响.首先结合已有的0.18µm单管实测数据对三维器件仿真模型的常规电学特性与总剂量效应相关参数进行校准，并针对大尺寸及深亚微米尺度SRAM单元，利用解析手段研究了表征SRAM单元单粒子翻转敏感性的特征量及其受累积辐照后的变化趋势.得到下述结论：只有当辐照阶段与单粒子作用阶段存储相反数值时，单元的单粒子翻转敏感性才会增强.基于校准后的0.18µm三维器件模型开展器件仿真工作，研究了累积辐照对于nMOS管单粒子脉冲形状的影响，结果主要体现为关断状态下瞬态单粒子脉冲初始值的显著增高.同时利用混合模拟详细计算了六管SRAM单元对应不同累积剂量情况下，离子分别入射四个中心单管时的电学响应变化.结果表明：只有当辐照阶段与单粒子作用阶段存储相反数值时，单元的单粒子敏感性才会增强，与解析分析的结论相一致.最后，针对参考文献中报道的部分不一致的测试结论给出了相应的推测并提供用于辅助的计算结果，初步判定是由于其他内部电路，最可能是同样包含对接反相器结构的灵敏放大器的影响所导致的.

[1]He B P，Ding L L，Yao Z B，Xiao Z G，Huang S Y，Wang Z J 2011Acta Phys.Sin.60 056105(in Chinese)[何宝平，丁李利，姚志斌，肖志刚，黄绍艳，王祖军2011物理学报60 056105]

[2]Zhang K Y，Guo H X，Luo Y H，He B P，Yao Z B，Zhang F Q，Wang Y M 2009Acta Phys.Sin.58 8651(in Chinese)[张科营，郭红霞，罗尹虹，何宝平，姚志斌，张凤祁，王园明2009物理学报58 8651]

[3]Knudson A R，Campbell A B，Hammond E C 1983IEEE Trans.Nucl.Sci.NS-30 4508

[4]Campbell A B，Stapor W J 1984IEEE Trans.Nucl.Sci.NS-31 1175

[5]He C H，Geng B，Wang Y P，Peng H L，Yang H L，Chen X H，Li G Z 2002Nucl.Electron.Detect.Technol.22 228(in Chinese)[贺朝会，耿斌，王燕萍，彭宏论，杨海亮，陈晓华，李国政2002核电子学与探测技术22 228]

[6]Schwank J R，Dodd P E，Shaneyfelt M R，Felix J A，Hash G L，Ferlet-Cavrois V，Paillet P，Baggio J，Tangyunong P，Blackmore E 2004IEEE Trans.Nucl.Sci.51 3692

[7]Schwank J R，Shaneyfelt M R，Felix J A，Dodd P E，Baggio J，Ferlet-Cavrois V，Paillet P，Hash G L，Flores R S，Massengill L W，Blackmore E 2006IEEE Trans.Nucl.Sci.53 1772

[8]Koga R，Yu P，Crawford K，George J，Zakrzewski M 2009IEEE Radiation Effects Data WorkshopQuebec，July 20—24，2009 p127

[9]Bhuva B L，Johnson Jr R L，Gyurcsik R S，Fernald K W，Kerns S E 1987IEEE Trans.Nucl.Sci.NS-34 1414

[10]Matsukawa T，Kishida A，Tanii T，Koh M，Horita K，Hara K，Shigeta B，Goto M，Matsuda S，Kuboyama S，Ohdomari I 1994IEEE Trans.Nucl.Sci.41 2071

[11]Integrated Systems Engineering Inc，2004 ISE TCAD Release 10.0 DESSIS manual，Switzerland