B/N掺杂对于石墨烯纳米片电子输运的影响*
邓小清 杨昌虎 张华林
(长沙理工大学物理与电子科学学院,长沙 410114)
(2013年3月31日收到;2013年6月4日收到修改稿)
1 引言
石墨烯是一种从石墨材料中剥离出的单层碳原子面材料,是碳的二维结构.自从2004年石墨烯被发现以来[1,2],引起了许多科学工作者的关注[3-14].目前实验和理论上研究较多的是将石墨烯裁剪成特定的纳米结构,使其形成功能性电子器件,如整流[6]、开关和负微分电阻效应[7]、自旋极化效应[8]、场效应管[9]以及巨磁阻效应[10]等.理想的石墨烯纳米带有两种边界类型:锯齿(zigzag)型[11-15]和扶手椅(armchair)型[16-18]边界.其中,锯齿型石墨烯纳米带(ZGNR)表现为金属电导性,并且呈现有趣的磁学特性;扶手椅型石墨烯纳米带(AGNR)的导电性取决于其宽度,宽度W满足3p-1,3p或3p+1(p为非零正整数)的不同AGNRs其电子结构区别较大,3p和3p+1型AGNRs分别具有中等和较宽带隙的半导体性质,但3p-1型AGNRs为窄带隙半导体[19,20].在对石墨烯的研究中,缺陷及掺杂对其结构和性能的影响一直受到人们的关注[21-27],B,C,N元素处在元素周期表的同一周期且彼此相邻,C—N和C—B是比较稳定的共价键,对石墨烯的B(N)掺杂能改变电子结构,进而影响其电子的输运特性[21-25].如N掺杂使得锯齿(zigzag)型石墨烯的能带结构中出现能隙,材料从金属转变为半导体[23];对三角形(zigzag)型石墨烯进行N-B成对掺杂后,石墨烯的电子输运显示出整流特性[24,25];利用化学气相沉积方法实现了对石墨烯的N原子掺杂,掺杂以后石墨烯的能带结构发生了明显变化[24,25];Kang等[8]用自旋极化密度泛函理论(DFT)理论研究了N(B)掺杂H2-ZGNR-H的电子结构和输运性质,发现N和B掺杂GNR可以调制电子自旋朝上和朝下状态的转换.一般来说,分子器件的输运性质主要与两类因素相关:一类是分子的本征特性,包括中心分子的空间构型以及所组成的原子的种类[18,24,25];另一类是分子与电极之间的界面特性,包括电极材料、电极构型以及分子与电极的耦合方式等[28-31].本课题组对N(B)掺杂的三角形石墨烯进行过研究,将石墨烯放入金电极之间,石墨烯与电极通过S原子连接,研究了不同尺寸器件下的整流行为,该整流主要来自于掺杂后N-B的原子极化形成类似于p-n结效应[24,25].考虑到三角形石墨烯的特殊性,作为该工作的延续,本文以矩形石墨烯为研究对象,以金作电极,石墨烯与电极之间通过S进行耦合,对石墨烯进行N(B)掺杂,主要考虑掺杂的位置、数目以及中心分子的空间构型(两石墨烯分子之间用烷链连接)对器件电子输运的影响.
本文采用基于DFT的非平衡格林函数(NEGF)方法,研究了锯齿(zigzag)型石墨烯纳米片夹在两金电极之间组成分子器件的输运性质,讨论石墨烯掺杂B和N原子对其输运性能的影响.
2 模型和方法
以锯齿(zigzag)型石墨烯纳米带为研究对象,以Au作为电极如图1所示,选用3×3的Au的(111)面模拟半无限大电极与分子间的相互作用.分子平面与Au的(111)面垂直,并通过末端S原子化学吸附于金属表面.整个体系包括三个部分,即左电极、右电极以及中心散射区域.中心散射区域由锯齿(zigzag)型石墨烯纳米片,S原子和每电极的两层金原子组成,这些金原子层用以屏蔽分子对电极的势扰动.体系M1和M2对应石墨烯纳米带左右两端的边缘分别掺杂2个和6个N原子和B原子;体系M3,M4和M5中,两石墨烯纳米带的中间用烷链连接,体系M3(M4,M5)分别掺杂1(2,7)个N原子和B原子.
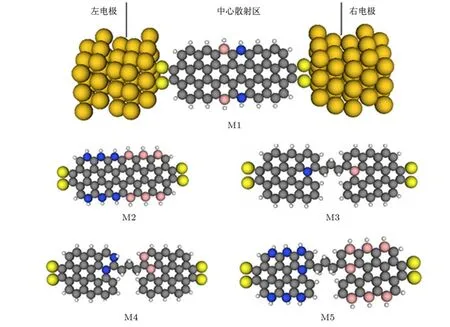
图1 石墨烯纳米片与Au电极组成的电极-分子-电极的结构示意图
体系的电流可以由Landauer-Buttiker公式求出[32,33]:

其中,uL和uR分别是左右电极的电化学势,Vb为左右两端的电压,Vb=(µR-µL)/2,µR=EF-Vb/2,µL=EF+Vb/2,[uL,uR]为能量积分区间,也称为偏压窗.由于计算中费米能处的能量设为零,[-Vb/2,+Vb/2]即为计算偏压窗,fL(E-µL)和fR(E-µR)是左右电极的费米分布函数;T(E,Vb)为能量E,外加偏压为Vb时体系的透射系数,可由下式求得


在本文的计算中,体系的几何结构优化、电子结构以及I-V特性的计算等均利用基于非平衡态格林函数和密度泛函理论的第一原理方法(ATK软件)[34,35].采用Quasi Newton算法优化时,每个原子上的作用力小于0.05 eV/˚A.Au电极原子的价电子轨道的基函数选为SZP(singleζ+polarization),其余原子的价电子轨道的基函数选为DZP(doubleζ+polarization),并通过 Siesta局域化数字轨道进行具体运算.对于Mesh cut-off,我们取150 Ry,Mesh cut-off主要控制实空间积分时网格划分的大小以及泊松方程的数值求解,其数值越高越接近真实值,但耗时也越长.原子实采用Troullier Martins赝势模型.电子交换关联势设为广义梯度近似(GGA-PBE).输运计算中传输方向上K取200,与传输方向垂直的另外两个方向上K点均取为1.
3 计算结果与讨论
3.1 电流-电压特性及整流系数
图2(a)和(b)分别为体系M1—M5分子器件在-1.6—1.6 V范围内的伏安特性曲线以及整流系数随偏压的变化,整流系数的定义采用:

R大于1为正向整流,反之为反向整流.如图2(a)所示,M1体系的电流在正偏压较负偏压下开启电流早,高偏压下电流比较接近,即低电压下呈现非对称性.M2体系的电流比较大,在负偏压下表现出负微分电阻现象.M3和M4体系表现出相似的电流-电压关系,正偏压下的电流明显大于对应的负偏压的电流,相对而言,M4的正向电流更大一些.低偏压下,M5体系在正负偏压下的电流均比较小.可以从整流曲线上看出,M3和M4体系表现出较好的整流效应,整个偏压下都是正向整流,其最大整流系数分别为60和214.M5体系的最大整流系数为85,整流系数变化太大,正向和反向整流都存在,与M2有点类似.M1在整个偏压下都是正向整流,但最大整流系数只有4左右.以上结果表明,石墨烯纳米带的电子输运性能与掺杂的浓度和掺杂位置是相关的.作为比较,我们也给出了M1和M3模型未掺杂前的石墨烯片与金电极构成分子器件在偏压下的电流-电压曲线,如图2(c)和(d)所示,Ma为M1未掺杂的分子器件,Mb为M3未掺杂的分子器件.可以看出,未掺杂的情况下,器件在正负偏压下的电流比较接近,没有整流发生,而且用烷链连接石墨烯片后的器件电流大大减小,比较掺杂前后模型的电子输运,发现B和N掺杂以后对电子的输运加强了,特别是正偏下的电流更加明显,主要是B(N)掺杂一方面改变了分子的电子结构,另一方面增加了器件中的载流子,包括空穴和电子.
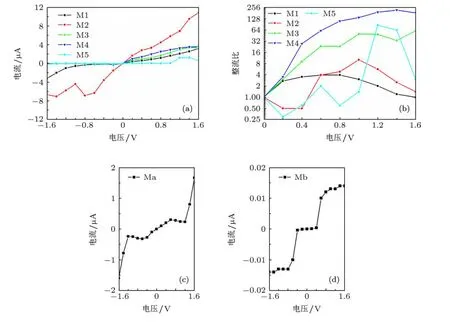
图2 M1—M5的(a)I-V和(b)整流曲线,(c)和(d)为M1和M3掺杂前的I-V曲线
3.2 体系的透射谱和MPSH分析
当分子与两电极形成双探针体系时,电子结构会由于分子与电极的耦合而受到影响,一部分分子的电子态扩展到了电极中,同时一部分电极的电子态扩展到分子中.特定能量的电极电子态具有确定的概率通过分子-电极结而进入另一电极,形成透射谱.由Landauer-Buttiker公式可知,通过分子器件的电流由偏压窗口中的透射系数T(E)所决定,透射系数反映了电子通过分子器件的传输性质,透射峰相应于电子通过分子态的共振透射概率.为了更清楚地理解分子体系的电子输运性质,图3给出了体系M1—M5体系在零偏压下的电子透射谱T(E)随能量变化的关系曲线.其中费米能级EF定为能量零点,由图可以看出,对于对应体系M1和M2,有两个明显的透射峰在费米能级附近,分别对应的最高占据分子轨道(HOMO)和最低未占据分子轨道(LUMO),因而在较低的偏压下就开启了较大电流.对于体系M3和M4,其HOMO(LUMO)透射峰比较低,体系M5的主要透射峰远离费米能级,因而在低偏压下的电流较小.

图3 平衡态下,M1—M5体系的透射谱
一般来说,透射系数与分子能级轨道有关,而对于分子体系的轨道分布,可以从分子投影自洽哈密顿量(MPSH)的分布来分析.MPSH是体系的自洽哈密顿在分子上的投影,与自由分子的哈密顿相比,它包含了左右电极对分子轨道的影响.为了重点分析整个开放系统中分子的HOMO和LUMO的空间分布,本文计算得到了MPSH对应的轨道.表1为平衡态下,模型M1—M5的HOMO和LUMO轨道的空间分布MPSH.可以看出,无论是HOMO还是LUMO轨道,都表现出一定的局域性分布,HOMO轨道主要局域在分子的右边部分,而LUMO轨道则主要局域在分子的左边部分,而这种局域的分布会导致偏压下电流的非对称性.由于模型M1和M2的轨道局域化程度相对其他体系要小一些,因而电子的透射也强些,对应图3透射谱上费米能级附近有较高的透射峰.
为了进一步分析整流效应,我们给出了M1,M3,M4和M5体系在偏压从-1.6 V到1.6 V每隔0.2 V的透射谱,为了特殊说明,我们把零偏压下的透射谱用红色曲线,具有最大整流对应的正负电压下的透射谱则用绿色和紫色曲线,如图4(a)—(d)所示.平衡态下,左右电极的电化学势相等,施加偏压会使它们发生变化,图中蓝色直线所夹的能量范围即为偏压窗.从图可知,随着偏压的变化,透射峰的位置和透射系数发生了较大的变化.对于M1体系来说,正负偏压下,随着偏压的增大,主要透射峰均向低能方向移动;低偏压下、正偏压下偏压窗内的透射峰高于负偏压.根据Landauer-Buttiker公式,电流的值为透射曲线与能量区间(偏压窗)积分的面积大小,正压电流较大,从而表现为正向整流,随着偏压进一步增大,负方向的透射很快增大,导致整流系数降低.M3和M4体系的透射谱有相似的特点,正偏压下,偏压窗内的透射谱明显高于负偏压下,相对而言,M4的正向偏压的透射更强,故整流系数最大.M5体系偏压窗内的透射系数比较小,负的低偏压下,偏压窗内的透射比正压下的强,表现为反向整流,当偏压增大到1 V以后,负偏压下的透射降低,而正偏压下,有3个透射峰进入偏压窗,整流变成了正向,特别是1.2 V时,整流系数达到最大为85,只是在1.6 V电压时,正向偏压的透射突然减少,导致整流效果减弱.可见,相比M3和M4,M5体系的整流是非常不稳定的.

表1 平衡态下体系M1—M5在HOMO和LUMO轨道上的MPSH分析
为了分析以上透射谱形成的机制,以M4体系为例,比较了零偏压和1.4 V(-1.4 V)下的主要透射谱对应的分子轨道和能级,如表2所示.零偏压下,费米能附近的透射谱主要由HOMO-1(-0.07 eV),HOMO(-0.02 eV),LUMO(0 eV)能级轨道产生.当偏压增加到1.4 V,能级轨道往负方向移动,变成 HOMO-1(-0.67 eV),HOMO(-0.6 eV),LUMO(0.55 eV),这三个轨道共同产生一个宽而高的透射峰,可以看出,相对零偏压,LUMO轨道的局域程度大大降低,有利于电子的透射.当偏压为-1.4 V时,不仅轨道 HOMO-1(-0.7 eV),HOMO(-0.07 eV),LUMO(0.3 eV)的位置发生了变化,更重要的是轨道分布变得更加局域,通道被抑制以至于在透射谱中有很小或者无透射峰显示.因此,该电压下这些轨道对应的透射系数很低.
对于M2体系在负偏压下的负微分电阻效应,我们给出了-0.8,-1.0和-1.2 V偏压下的透射谱.如图5所示,在-0.8 V偏压下,偏压窗[-0.4 V,0.4 V]内,有一个宽而高的透射峰P1(对应的分子轨道是比较离域分布),还有P2和部分P3;当偏压增加到-1.0 V时,尽管偏压窗增大,并且进入窗内的透射峰增加了.但是,由于P1对应轨道的局域化,导致该能量处的透射系数明显降低,根据电流的计算公式(3),该偏压下电流比-0.8 V下的电流要小得多;随着偏压进一步增加到-1.2 V,透射峰P1继续降低,对应的分子轨道非常局域,近似于被抑制,但是P2和P3完全进入了偏压窗,并且具有较高的透射系数,因此-1.2 V偏压下的电流比-1.0 V下增大了.综上所述,M2体系中的负微分电阻现象主要由于偏压导致透射峰的改变,并且在某些偏压下主要透射通道被抑制而引起.

图4 体系M1,M3,M4和M5在-1.6—1.6 V偏压下的透射谱图,电压间隔为0.2 V,蓝色直线所夹的能量区域为偏压窗

表2 在0 V和1.4 V(-1.4 V)时,体系M4在HOMO(HOMO-1)和LUMO轨道上的MPSH分析

图5 体系M2在-0.8,-1.0和-1.2 V偏压下的透射谱
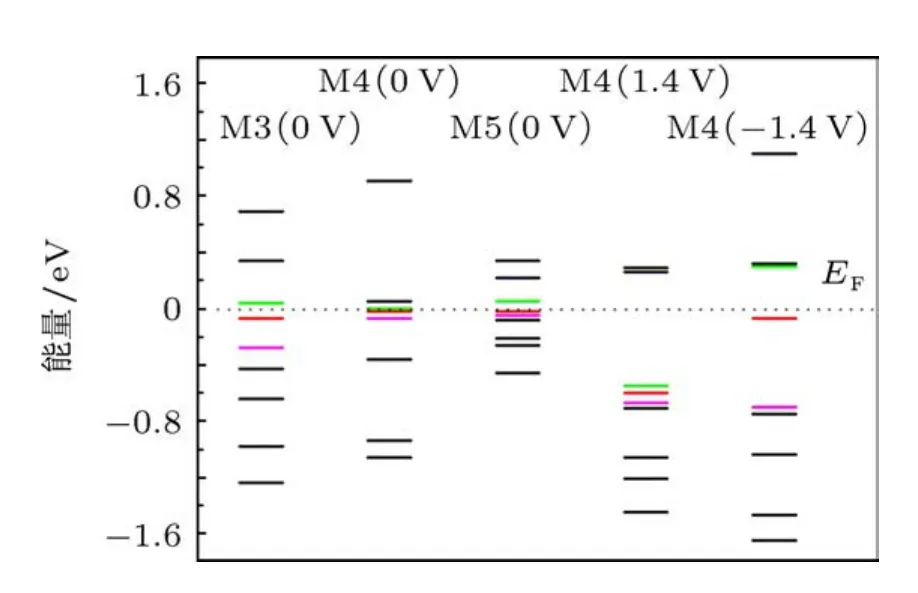
图6 体系M3,M4,M5在零偏压下和M4在1.4 V(-1.4 V)偏压下的能谱
最后计算了M3—M5体系的中心分子的能谱,为了方便区分,HOMO-1,HOMO和LUMO分别用紫色、红色和绿色的短线标出,如图6所示.由于掺杂会使得更多的电子从电极进入中心分子[36],因而导致分子的能级移动,导致费米能级附近的能级轨道也不同,掺杂N(B)原子较多的体系比较少体系的能级间距更小,正负电压下,这些轨道的移动也会不同.以M4为例,-1.4 V下,LUMO越过了费米能级,移到-0.67 eV,而1.4 V下,LUMO能级为0.3 eV,HOMO则为-0.07 eV.可见由于掺杂的位置的数量的不同,导致分子轨道分布有差异,而正负偏压也会导致轨道发生不同的移动,再加上某些偏压下轨道会受到抑制,因此就会有不同的电子输运性能.
4 结论
利用基于密度泛函理论的第一性原理方法,对锯齿(zigzag)型石墨烯纳米片进行N(B)掺杂,在纳米片的边缘掺杂N(B)原子,发现电流-电压具有非线性行为,但是整流系数较小,特别是掺杂较多时,整流具有不稳定性.而用烷链把两个石墨烯片连接,在烷链附近和石墨烯片的边缘进行N(B)掺杂,发现在烷链附近掺杂具有较大的整流,但是掺杂的原子个数和位置会影响整流性能.研究表明:整流主要为正负电压下分子能级的移动方向和空间轨道分布不同导致.部分体系中的负微分电阻现象主要由于偏压导致能级移动和透射峰形态的改变,并且在某些偏压下主要透射通道被抑制而引起.
[1]Zhang Z H,Peng J,Zhang H 2001Appl.Phys.Lett.79 3515
[2]Zhang Z H,Peng J,Huang X 2002Phys.Rev.B 66 085405
[3]Zhang Z H,Yuan J,Qiu M 2006J.Appl.Phys.99 104311
[4]Zhang Z H,Yang Z,Wang X,Yuan J,Zhang H,Qiu M,Peng J 2005J.Phys.:Condens.Matter17 4111
[5]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004Science306 666
[6]Zeng M,Shen L,Yang M,Zhang C,Feng Y 2011Appl.Phys.Lett.98 053101
[7]Masum Habib K M,Zahid F,Lake R K 2011Appl.Phys.Lett.98 192112
[8]Kang J,Wu F,Li J 2011Appl.Phys.Lett.98 083109
[9]Soudi A,Aivazian G,Shi S F,Xu X D,Gu Y 2012Appl.Phys.Lett.100 033115
[10]Zeng M,Huang W,Liang G 2013Nanoscale5 200
[11]Zheng X H,Wang X L,Huang L F,Hao H,Lan J,Zeng Z 2012Phys.Rev.B 86 081408
[12]Zheng X H,Wang X L,Abtew T A,Zeng Z 2010J.Phys.Chem.C 114 4190
[13]Zheng X H,Song L L,Wang R N,Hao H,Guo L J,Zeng Z 2010Appl.Phys.Lett.97 153129
[14]An Y P,Yang Z Q 2011Appl.Phys.Lett.99 192102
[15]Jin F,Zhang Z H,Wang C Z,Deng X Q,Fan Z Q 2013Acta Phys.Sin.62 036103(in Chinese)[金峰,张振华,王成志,邓小清,范志强2013物理学报62 036103]
[16]Ouyang F P,Xu H,Lin F 2009Acta Phys.Sin.58 4132(in Chinese)[欧阳方平,徐慧,林峰2009物理学报58 4132]
[17]Xu JM,Hu X H,Sun LT2012Acta Phys.Sin.61027104(in Chinese)[许俊敏,胡小会,孙利涛2012物理学报61 027104]
[18]Zheng J M,Guo P,Ren Z,Jiang Z,Bai J,Zhang Z 2012Appl.Phys.Lett.101 083101
[19]Yao Y X,Wang C Z,Zhang G P,Ji M,Ho K M 2009J.Phys.:Condens.Matter21 235501
[20]Son Y,Cohen M L,Louie S G 2006Phys.Rev.Lett.97 216803
[21]Zeng J,Chen K Q,He J,Zhang X J,Hu W P 2011Organic Electronics12 1606
[22]Zeng J,Chen K Q,He J,Fan Z Q,Zhang X J 2011J.Appl.Phys.109 124502
[23]Lin Q,Chen Y H,Wu J B,Kong Z M 2011Acta Phys.Sin.60 097103(in Chinese)[林琦,陈余行,吴建宝,孔宗敏2011物理学报 60 097103]
[24]Deng X Q,Zhang Z H,Tang G P,Fan Z Q,Qiu M 2012Appl.Phys.Lett.100 063107
[25]Deng X Q,Tang G P,Guo C 2012Phys.Lett.A 376 1839
[26]Wei D C,Liu Y Q,Wang Y,Zhang H L,Huang L P,Yu G 2009Nano Lett.9 1752
[27]Guo B D,Liu Q,Chen E D,Zhu H W,Fang L,Gong J R 2010Nano Lett.10 3079
[28]Tworzydlo J,Trauzettel B,Titov M,Rycerz A,Beenakker C W J 2006Phys.Rev.Lett.96 246802
[29]Schomerus H 2007Phys.Rev.B 76 045433
[30]Zhang G P,Qin Z J 2011Chem.Phys.Lett.516 225
[31]Hu S J,Du W,Zhang G P,Gao M,Lu Z Y,Wang X Q 2012Chin.Phys.Lett.29 057201
[32]Landauer R 1970Philos.Mag.21 863
[33]B¨uttiker M 1986Phys.Rev.Lett.57 1761
[34]Zhang Z H,Qiu M,Deng X Q,Ding K H,Zhang H 2009J.Chem.Phys.130 184703
[35]Zhang Z H,Deng X Q,Tan X Q,Qiu M,Pan J B 2010Appl.Phys.Lett.97 183105
[36]Zhang Z H,Guo C,Kwong G,Deng X Q 2013Carbon51 313

