基于Fisher信息理论的突变检测新方法*

蔡舒平 戴理 倪淏

1)(江苏大学电气信息工程学院，镇江 212013)

2)(江苏大学，机械工业设施农业测控技术与装备重点实验室，镇江 212013)

(2013年1月8日收到;2013年6月14日收到修改稿)

1 引言

由于自然界本身和人类活动的加剧，许多复杂系统如生态系统、气象系统等常常表现为从一个相对稳定状态翻转到另一个相对稳定状态的现象.生态系统中一个典型的例子是在一个浅水湖泊中，由于磷的流入，生态系统有可能从一个寡营养状态翻转到一个富营养状态而导致藻类过度生长，进而由于缺乏鱼类生存所需要的氧气而使生物的多样性减少和水质量恶化，随之而来的是系统的大部分功能和效用丧失.气候系统中如全球气候在温暖而潮湿的间冰期和凉爽而干燥的冰川期之间快速地翻转等等.近年来，对复杂系统状态翻转的研究因其对现代社会的影响而引起了人们广泛的关注.科学工作者通过深入研究后发现，所有这些系统的状态翻转具有一个共同的特征，那就是其内在的动力学结构随着外强迫作用的变化而发生了突变.因此，有关动力学结构突变检测的研究近年来受到了普遍重视，其中气候系统因其本身的复杂性及与人类日常生活的密切相关性，使得在这方面的研究显得尤为迫切.

封国林等[1]从气候突变的检测和研究、气候资料信息的提取和分离、气候系统复杂性的研究、气候系统动力学结构特征及极端气候事件的检测等5个方面阐述了近年来在我国气候突变检测技术研究方面所取得的新进展.传统的检测方法如滑动t-检验，Cramer法，Yamamoto信噪比法以及Mann-Kendall(M-K)法等，在突变检测的早期得到了广泛应用，然而由于这些传统方法自身固有的一些缺陷使得在实际检测中所得结果均存在不同程度的突变点漂移，在此情况下，一些新的检测方法如分割方法(即BG算法)应运而生，龚志强等[2]对此进行了实际检验和应用，并得到了一些有益的结果.近年来，国内学者如封国林、龚志强、何文平、王启光和侯威等人将非线性科学的一些研究成果应用于动力学结构突变检测中，分别提出了动力学相关因子指数法[3]、动力学指数分割算法[4]、滑动去趋势波动算法[5]、排列熵算法[6]、近似熵算法[7]、滑动移除近似熵算法[8]、重标极差法[9]等检测方法.成海英等[10]将偏度系数和峰度系数引入时间序列的突变检测中，提出了基于概率密度分布型变化的突变检测方法.此外，还有学者将小波分析、粒子滤波等方法用于突变检测中[11,12].在与气候突变有关的其他研究领域，龚志强等[13]把希尔伯特-黄变换(Hilbert-Huang transform，HHT)应用于气候资料信息的分离和提取中，且与小波变换进行了对比分析，并针对它们各自的缺点提出了可能改进的措施.与此同时，封国林等[14]介绍了一种能判断不同时间序列之间动力学异同性的条件熵算法，讨论了其物理意义，并以长三角地区为例，验证了这一算法的有效性和可靠性.万仕全等[15]利用Q指数来识别时间序列之间动力结构的异同性，并利用该方法分析了几种典型代用资料的动力学结构，得到了一些有益的结果.而在极端气候事件的检测方面，封国林等[16]利用固定阈值法研究了Lorenz系统极端事件序列的长程相关性特征，并在此基础上分析了实际的气象观察资料，得到了一些有参考价值的结论.所有这些研究工作极大地丰富了突变检测方法，拓宽了突变检测的途径.然而，由于所研究问题的复杂性，不可能存在一种万能的方法一劳永逸地解决所有问题，因此，人们从未停止过对突变检测新思想、新方法的探寻，尤其是分析那些已被噪声污染且稀疏的实际野外观察数据方法的研究.

实际中往往会面临单变量的一维时间序列，很显然，系统的非线性突变特征信息就蕴藏在这些序列中，如何有效地从中提取这类信息成为一个非常关键的问题.

Fisher信息(FI)恰好为我们提供了表征这样一类突变特征信息的可能性.原因是任何类型的数据和模型本质上都可以转换为信息而不管最初的学科是什么[17].不像系统信息的其他测量方法，Fisher信息提供了一种通过监测系统变量从而监测系统的状态和状态突变的方法[18]，这种检测状态和状态突变的能力使得识别发生在系统中的最根本的变化成为可能.事实上，Frieden[19,20]使用该理论推导出了许多基本的物理学、热力学、人口遗传学方程.近年来，生态学家广泛使用Fisher信息理论来研究生态领域的问题，Fath等[18]和Mayer等[21]使用Fisher信息来作为一种复杂生态系统动态秩序的度量.Mayer等[21]和Karunanithi等[22]提议用来作为一种量化的指标来检测和评估生态系统状态的翻转以及作为一种可持续性标准[23].Fisher信息还被用于研究包含一个多间隔食物链稳定性问题的模型系统[24-26]以及用于可持续环境管理中的动态模型系统的优化控制问题[26,27].Rico-Ramirez等[28]把Fisher信息应用于医疗化工领域的优化控制问题.在了解了以上为研究生态系统尝试使用Fisher信息理论所取得的成果后，本文试图用它来解决动力学结构的突变检测问题.

2 方法

2.1 Fisher信息

统计学家Ronald Fisher在1922年提出了一种度量不确定性的方法，即现在称之为费歇信息[29].然而，由于信息只能从代表现行动力系统稳定性的数据中获得，使得Fisher信息尤其被认为是一种对现行动力系统秩序的度量.许多文献已经展示了使用Fisher信息来度量生态系统的秩序的能力[21,22,30].一个变量单次测量的Fisher信息I计算如下：

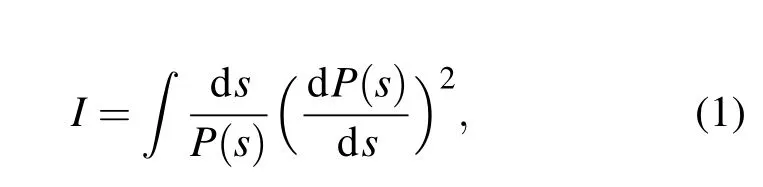
这里P(s)为概率密度函数(PDF)，s是一个状态变量.

对于一个稳定的动力系统而言，系统变量的概率密度分布也较为稳定，而当动力学结构发生变化后，系统变量的概率密度分布也会发生不同程度的变化.由于Fisher信息是基于概率密度函数的导数，因此它反映的是一种局部特性，这使得它能敏锐捕捉系统变量的概率密度分布发生微小的变化.鉴于此，本文用它检测和识别蕴藏在时间序列中的突变特征，为突变检测提供一种新的途径.

实际计算中，为了避免因除以较小的P(s)值而带来的计算误差，我们用一个变量的强度来代替(1)式中概率密度函数P(s)，即令q2(s)=P(s)，于是(1)式变为

为了使(2)式适合于分析和检测实际系统的观察序列，我们用求和来代替积分以及用差分来代替微分，即用ΔS=Si-Si+1和Δq=qi-qi+1来分别代替ds和dq，从而Fisher信息能被近似为

(3)式中，Si代表系统的某一个特定状态，即S1代表状态1，S2代表状态2等等.于是：Si-Si+1=1，则计算Fisher信息的最终表达式为

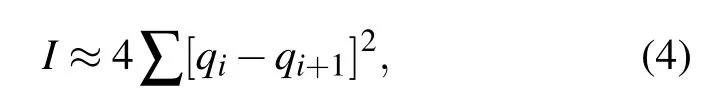
表达式(4)将会用于我们以下所有的计算.

2.2 Fisher信息的计算

检测系统动力学结构突变的第一步是获取描述系统状态随时间变化的观察数据序列集，然后在数据集上定义一个滑动时间窗口，窗口宽度取决于可得到的数据量和系统的行为.按照经验，窗口宽度至少应该包含8个数据点以确保窗口中的每一点不会过度影响整个计算.窗口的滑动因子应小于窗口宽度，这样相邻的窗口间就会出现一个重叠，这样做的好处是能够捕获有可能已经延伸到该窗口边界之外的动力学结构的突变.

即若设观察数据序列集为D={d(k),k=1,···,N}，其中N为序列总长度，窗宽为w∈N，滑动因子为δ∈N，用数学公式可把滑动窗W描述如下：

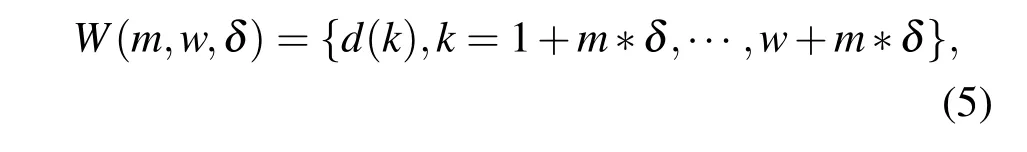
式中m=1，2，···，M，M为窗口个数，M=(N-w)/δ.

在把时间序列转变为一个重叠窗口序列以后，接下来是将每个滑动窗口划分成如下I个区间：

式中{Zi=[Si-1,Si),i=1,2,···,I}，互不相交.

则数据d(k)∈W(m,w,δ)落入区间Zi的概率P(Zi)等于d(k)∈W(m,w,δ)落入区间Zi的数目与W(m,w,δ)中总数据个数w之比值.

即使用如下公式计算窗口中相应于Zi区间上的概率密度分布P(Zi)：

需要说明的是，在上述计算中，窗口中区间个数I的取值越大，区间越窄，相同条件下，所计算出的窗口概率密度分布比较平缓，从而Fisher信息值较小，这使得其对突变的反应不够敏感.反之，I取值越小，区间越宽，相同条件下，所计算出的窗口概率密度分布比较陡峭，从而Fisher信息值较大，而这又容易受到噪声的干扰而引起误判.一般情况下，I的取值应根据待分析数据的最大波动范围而定.

接下来，为每个状态计算q(Zi)(q(Zi)=以及使用(4)式为每个时间窗口估计FI.值得注意的是计算的FI值被分配给每个时间窗口的末端位置.

归纳起来，计算FI的基本步骤如下：1)把时间序列数据划分为一连串重叠的时间窗口，2)把每个时间窗口划分成长度相等的若干个区间，清点落入每个区间的数据个数;3)计算相应于该窗口的概率密度分布;4)对每个时间窗口使用Fisher信息实用计算公式从概率密度函数中计算Fisher信息.

3 结果

3.1 FI方法在理想时间序列中的性能测试

在所有的突变测试函数中，正余玄复合函数因其构造简单，表现形式多样，物理意义明确而得到了广泛的应用.为了便于对照，本文亦选择它为测试函数来检验新方法的有效性.

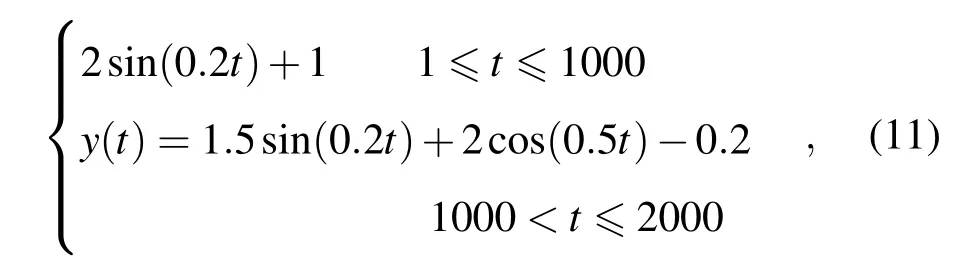
(11)式表明，上述时间序列来自两种不同的动力学结构，在区间[1，1000]上，由单一的正玄函数所组成，在区间(1000，2000]上，由正余玄函数复合而成.很显然，在t=1000时，系统从一种形式的动力学结构突变为另一种形式的动力学结构.图1(a)给出了该理想信号序列波形.为了进一步测试新方法的抗噪能力，在原理想信号的基础上，同时构造如下两种形式的加噪信号.图1(b)为加入信噪比为30 dB高斯白噪声后信号波形，图1(c)为随机加入12个尖峰噪声后的信号波形，其大小在2—5之间变化.

图2为采用Fisher信息方法在滑动窗口宽度w=20，滑动步长δ=1情况下，对3种信号进行突变检测所得结果.

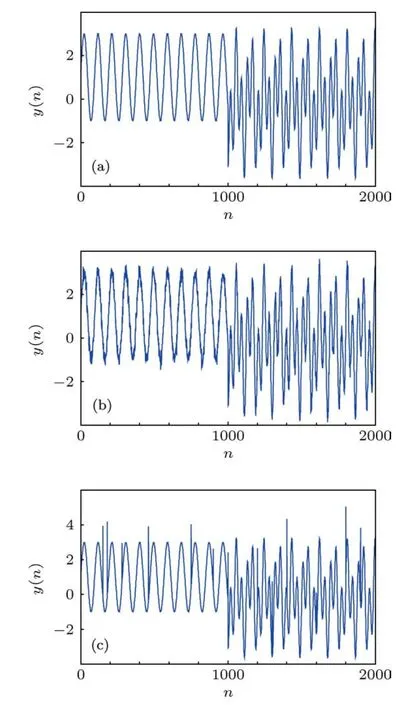
图1 测试信号 (a)理想信号;(b)加白噪声的理想信号;(c)加尖峰噪声的理想信号

从图2(a)所呈现的检测结果可以看出，在区间[1，1000]上，FI值表现出疏密有致的有规律波动，而在区间(1000，2000]上，FI值表现出疏密不等的无规律变化，在n=1000处，出现了一个幅度为4(最大的FI值)的尖峰.而由Fisher信息的定义可知，Fisher信息是基于序列概率密度分布的导数，这意味着在上述两个区间上，序列的概率密度分布肯定不同，这种不同意味着在整个区间[1，2000]上，序列的概率密度分布在n=1000处会出现一次“跃变”.我们知道，跃变函数的一阶导数刚好是冲击函数，这就不难理解为什么在n=1000处会出现一个尖峰冲击.由此看来，基于Fisher信息的突变检测方法深刻地揭示了突变发生的机理，如实地反映了突变发生的整个物理进程.另一方面，Fisher信息又是一种对信号稳定程度的一种度量，从这一点来讲，突变前序列的稳定性要优于突变后.

从图2(b)的测试结果来看，该方法具有一定的抗噪能力.和图2(a)相比较，突变前后因其噪声的加入使得在一定程度上会影响序列的概率密度分布，又因为Fisher信息是基于概率密度分布的导数，反映的是一种局部特性，因此，它对任何影响序列概率密度分布发生微小变化的因素较敏感，其结果是突变前后FI值较图2(a)出现了一定程度的波动，尤其是突变前，FI值呈现出一种毫无规律的小幅尖峰震荡.但该方法对噪声的这种敏感性仅限于此，丝毫不会影响突变检测的最终结果，这一点从图2(b)的FI分布趋势与图2(a)中完全一致就说明了这一点.

图2 三种信号的FI突变检测 (a)理想信号;(b)加白噪声信号;(c)加尖峰噪声信号

图2(c)展示的该突变检测方法抗尖峰噪声的能力.从图中可以看到，信号中的尖峰噪声仅仅会对突变前后FI值造成轻微的影响，并使突变点n=1000处FI值的跃变幅度有所减弱，尽管如此，从图中仍可以清楚地识别出突变点.有趣的是尖峰噪声对突变前后FI值的影响恰好与白噪声相反，这是由FI值的计算方法所决定的.FI是以窗口为单位进行计算的，单个的尖峰噪声对整个窗口的影响被平均掉了，这样看来，窗口中的单一信号比复合信号能更有效地抑制尖峰噪声的影响，这也就是图2(c)中所看到的突变前FI的变化要比突变后FI的变化更平稳的原因.

在以上测试过程中，子序列长度即窗口宽度固定为一个特定的值(w=20)，得出了完全相同的突变检测结果.由此引出了另外一个问题，那就是对于任意的子序列长度检测结果是否仍然完全相同呢?为此，需要考察不同子序列长度下该方法对同一信号的突变检测结果.

图3给出了子序列长度分别取10，50，100和200时，对理想信号的突变检测结果.

从图3不难看出，四种不同情况下，FI的演化规律完全类似，即以突变点为界，FI划分为两个明显不同的演化阶段，在两个不同阶段的衔接处即为突变点，此处的FI值表现为一个急促向上的跳变，跳变幅度及突变前后FI波动幅度随着子序列长度的增加有所减弱，这是因为子序列取得越大，子序列中的单个数据点对由整个子序列计算出来的FI值的影响愈小，FI值愈稳定，但这丝毫不会影响最终的检测结果.不同子序列长度下检测结果的一致性，表明了该方法的检测结果不依赖于子序列长度.

图3 理想序列FI突变检测 (a)w=10;(b)w=50;(c)w=100;(d)w=200

一种方法之所以被提出必有其不同于传统方法的独特之处.为此，有必要把该方法与一些传统方法进行比较，以检验其有效性.仍以上述线性理想序列为例，分别基于滑动t检验和Yamamoto法对该序列进行检测，其中子序列长度取200，滑动步长取1，图4所示为这两种方法的检测结果.

在图4(b)和(c)中，对应突变点t=1000，滑动t检验和Yamamoto法均给出了一个明显的突变区域(800—1200之间)，在突变点附近，无论t值还是信噪比均出现了最大值，且超过了0.01显著性水平.然而，若想进一步准确定位突变点则存在一定的困难.而由FI法在此种情况下所给出的检测结果中(见图3(d))，对突变点的检测能够做到准确定位.

进一步考察当子序列的长度取不同值时，滑动t检验和Yamamoto法的检测结果是否仍然保持一致.图5给出了当子序列长度取20，滑动步长取1时，滑动t检验和Yamamoto法对此的检测结果.

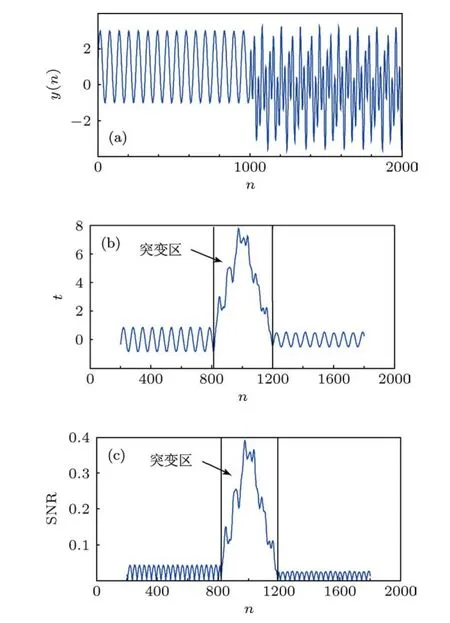
图4 子序列长度取200时检测结果 (a)理想序列;(b)滑动t检验;(c)Yamamoto法

从图5中可以看出，尽管滑动t检验和Yamamoto法在此情况下仍能对突变点做出一定的反应，但要对检测结果做出合理的解释已变得不可能;而FI法在此种情况下对突变点的检测结果(见图2(a))未发生任何改变.改变子序列的长度(如取50，100)会得出类似的结果(图略).同时对在本质上也是基于均值思想的传统检测方法——Crammer法也进行了类似的实验，发现存在同样的问题.而另一种传统检测方法——M-K法常常被用来检测序列中的趋势突变，若时间序列中不存在明显的趋势突变，则对此序列中动力学结构突变的检测就无从谈起.综合对比以上检测实验结果和分析可知，FI法无论在对动力学结构突变检测的准确性还是稳定性方面较传统方法均具有明显的优势.

3.2 FI方法在实际气象观察资料中的应用

图5 子序列长度取20时检测结果 (a)理想序列;(b)滑动t检验;(c)Yamamoto法

气候系统具有典型的时空多尺度、结构多层次、本质非线性特征，不同层次之间关系及其相互作用十分复杂[31].自从Lorenz[32,33]和Charney等[34]从理论上论证了气候突变存在的可能性，有关气候突变的研究得以广泛开展.按照控制气候系统的动力学方程是否发生变化将气候突变分为动力学结构突变和气候状态变量在统计意义上发生了显著变化的突变，如均值突变、趋势突变等.传统的突变检测方法如滑动t-检验，Cramer法，Yamamoto法以及M-K法等均是基于状态变量在统计意义上的显著变化来判断突变的发生，其检测结果均具有多尺度特征.然而系统的动力学结构突变发生的时间与特定的时间尺度没有必然的关联，因此基于系统状态变量在统计意义上的显著变化来判断突变的传统检测方法不能够对系统的动力学结构突变进行有效识别[5].近年来，一些新的突变检测方法如近似熵(ApEn)算法，Q算法等用于检测气候系统的动力学结构突变均取得了一定的效果.然而随着人们对复杂气候系统愈来愈多的了解和掌握，一些原先未曾认识到的问题逐渐暴露了出来，人们迫切需要探寻新的突变检测方法来应对不断涌现的新情况、新问题.因此，有关气候系统的动力学结构突变检测问题一直处于持续的研究和探索中.

气候系统中的两大气象要素温度和降水是两个最能体现气候动力学结构发生突变的量，因此，本文采用两大气象要素之一的温度来检验本文所提方法在检测气候系统动力学结构突变中的有效性.文中所用数据来自中国气象局国家气象信息中心“西北地区地面气候资料日值数据集”兰州站1960—2008年日平均气温资料.图6给出了该观察站1960—2008年逐日平均气温的FI检测结果.

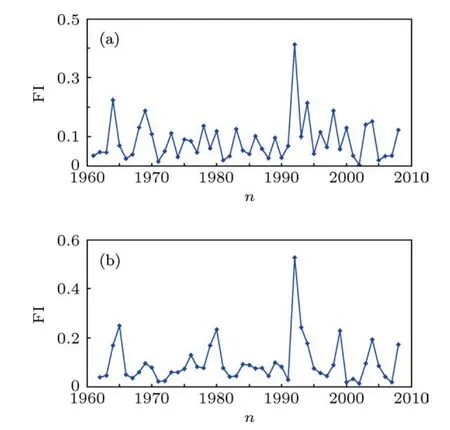
图6 兰州站逐日平均温度序列FI变化情况 (a)子序列长度取365 d(1年);(b)子序列长度取730天(2年)

从图中可以看出，20世纪90年代初该观察站日均温度发生了一次明显的突变，这与已有该站所在地区历史上日均温度突变年份的研究结果相一致[35,36].另一方面，从图6中子序列长度取1年和2年时，所检测到的突变点相一致来看，进一步表明该方法所得检测结果不依赖于子序列的长度.

4 讨论与结论

本文引入常被用来检测生态系统稳定性和生态状态翻转的指标——Fisher信息来识别和检测系统动力学结构突变，是因为本文紧扣Fisher信息是基于概率密度分布的导数这一基本原则.基于不同动力学性质的数据其概率密度分布大小不同，而具有相同动力学性质的数据其概率密度分布差异不大.因此，当系统的动力学结构发生突变时，基于突变前后两种不同动力学结构的数据其概率密度分布肯定会发生不同程度的改变.这种细微的改变恰好通过Fisher信息加以定格和放大.因此，理论上Fisher信息是对动力学结构突变的一种很好的测量.

本文首先将它用于分析理想时间序列，结果表明该方法能够准确定位突变点，并且具有良好的抗噪性能，同时，检测结果不依赖于子序列长度的选择.紧接着，比较了新方法与传统检测方法的检测效果，彰显了新方法的优越性.最后，应用于“西北地区地面气候资料日值数据集”兰州站1960—2008年(49年)日平均气温资料，发现检测结果与已有该站所在地区历史上日均温度突变年份的研究结果完全符合，进一步展示了该方法的有效性和实用性，表明该方法在动力学结构突变检测中的应用前景和实用价值.

不像在研究气候时空分布时那样需要做时空插值，由于受观察资料的限制，边界效应是一个不容忽视的问题.而本方法是按照所给时段内的观察数据，采用滑动窗技术逐点计算FI值，并把计算结果分配给窗口的末端，这就意味着对突变点的真正检测是从观察数据的第L点开始的(L为窗口宽度即子序列长度)，对前L-1点上的突变检测无法进行，这是基于滑动窗技术的此类检测方法的一个共性问题(包括滑动t检验，Yamamoto法和Crammer法等基于子序列均值的传统检测方法).

本方法可用于检测任何时间尺度的观察数据序列，观察数据的时间尺度仅仅影响检测的精度即分辨率.

[1]Feng G L，Gong Z Q，Zhi R 2008Acta Metrol.Sin.66 892(in Chinese)[封国林，龚志强，支蓉2008气象学报66 892]

[2]Gong Z Q，Feng G L，Wan S Q，Li J P 2006Acta Phys.Sin.55 477(in Chinese)[龚志强，封国林，万仕全，李建平2006物理学报55 477]

[3]Feng G L，Gong Z Q，Zhi R 2006Nonlinear Theories and Methods on Spatial Temporal Distribution of the Observational Data(Beijing：China Meteorological Press)pp1—100(in Chinese)[封国林，龚志强，支蓉2006观察数据时空分布的非线性理论和方法(北京：中国气象出版社)第1—100页]

[4]Gong Z Q，Feng G L，Dong W J 2006Acta Phys.Sin.55 3180(in Chinese)[龚志强，封国林，董文杰2006物理学报55 3180]

[5]He W P，Wu Q，Zhang W，Wang Q G，Zhang Y 2009Acta Phys.Sin.58 2862(in Chinese)[何文平，吴琼，张文，王启光，张勇2009物理学报58 2862]

[6]Hou W，Feng G L，Dong W J，Li J P 2006Acta Phys.Sin.55 2663(in Chinese)[侯威，封国林，董文杰，李建平2006物理学报55 2663]

[7]Wang Q G，Zhang Z P 2008Acta Phys.Sin.57 1976(in Chinese)[王启光，张增平2008物理学报57 1976]

[8]He W P，He T，Cheng H Y，Zhang W，Wu Q 2011Acta Phys.Sin.60 049202(in Chinese)[何文平，何涛，成海英，张文，吴琼2011物理学报60 049202]

[9]He W P，Deng B S，Wu Q，Zhang W，Cheng H Y 2010Acta Phys.Sin.59 8264(in Chinese)[何文平，邓北胜，吴琼，张文，成海英2010物理学报59 8264]

[10]Cheng H Y，He W P，He T，Wu Q 2012Acta Phys.Sin.61 039201(in Chinese)[成海英，何文平，何涛，吴琼2012物理学报61 039201]

[11]Babak A S，Krishnaprasad P S 2004EURASIP J.Appl.Signal Processing15 2295

[12]Abhisek U，Rastko Z 2006Electric Power System Research76 815

[13]Gong Z Q，Zou M W，Gao X Q，Dong W J 2005Acta Phys.Sin.54 3947(in Chinese)[龚志强，邹明玮，高新全，董文杰2005物理学报54 3947]

[14]Feng G L，Hou W，Dong W J 2006Acta Phys.Sin.55 962(in Chinese)[封国林，侯威，董文杰2006物理学报55 962]

[15]Wan S Q，Feng G L，Dong W J，Li J P 2005Acta Phys.Sin.54 5487(in Chinese)[万仕全，封国林，董文杰，李建平2005物理学报54 5487]

[16]Feng G L，Wang Q G，Hou W，Gong Z Q，Zhi R 2009Acta Phys.Sin.58 2853(in Chinese)[封国林，王启光，侯威，龚志强，支蓉2009物理学报58 2853]

[17]Cabezas H，Fath B D 2002Fluid Phase Equilibria194–197 3

[18]Fath B，Cabezas H，Pawlowski C W 2003J.Theor.Biol.222–224 517

[19]Frieden B R 1998Physics from Fisher Information：A Unification(Cambridge，UK：Cambridge University Press)

[20]Frieden B R 2001Probability,Statistical Optics and Data Testing(3th Ed.)(New York：Springer-Verlag)

[21]Mayer A L，Pawlowski C W，Cabezas H 2006Ecol.Model.195 72

[22]Karunanithi A T，Cabezas H，Frieden B R，Pawlowski C W 2008Ecol.Soc.13 22

[23]Fath B D，Cabezas H 2004Ecol.Model.174 25

[24]Cabezas H，Pawlowski C W，Mayer A L，Hoagland N T 2005J.Clean.Product.13 455

[25]Cabezas H，Pawlowski C W，Mayer A L，Hoagland N T 2005Resources,Conservation and Recycling44 279

[26]Shastri Y，Diwekar U，Cabezas H 2008Environ.Sci.Technol.42 5322

[27]Shastri Y，Diwekar U，Cabezas H，Williamson J 2008Environ.Sci.Technol.42 6710

[28]Rico-Ramirez V R，Qunitana-Hernandez P A，Ortiz-Cruz J A，Hernandez-Castro S 2008Computer-Aided Chem.Engin.25 1155

[29]Fisher R A 1922Philosoph.Trans.Roy.Soc.London222 309

[30]Eason T，Cabezas H 2012J.Environ.Manage.94 41

[31]Li Y Q 2001Plateau Meteorol.20 88(in Chinese)[李跃清2001高原气象20 88]

[32]Lorenz E N 1963J.Atmos.20 130

[33]Lorenz E N 1976Quat.Res.6 495

[34]Charney J G，Devore J G 1979J.Atmos.Sci.36 1205

[35]Wei F Y，Cao H X 1995Sci.Atmos.Sin.19 140(in Chinese)[魏凤英，曹鸿兴1995大气科学19 140]

[36]Zhao F F，Xu Z X 2006Sci.Atmos.Sin.64 246(in Chinese)[赵芳芳，徐宗学2006气象学报64 246]