关于古塔变形研究的数学模型

唐纪芳，张子卫

（四川职业技术学院,四川 遂宁 629000）

关于古塔变形研究的数学模型

唐纪芳，张子卫

（四川职业技术学院,四川 遂宁 629000）

我国是一个文明古国，各地的古塔建筑非常的多，由于长时间承受自重、气温、风力等各种作用，偶然还要受地震、飓风的影响，古塔会产生各种变形，诸如倾斜、弯曲、扭曲等.为保护古塔，文物部门需适时对古塔进行观测，了解各种变形量，以制定必要的保护措施.本文通过对古塔测量数据进行分析研究，对古塔各层的中心、变形的塔身倾斜度、扭曲度、古塔弯度等给出了明确的定义，并运用数学软件进行了相应计算，对古塔的各个测试时间的变形程度给出了具体量化结论，并建立了古塔变形的数学模型预测其变形趋势，给文物管理部门提出了有关古塔保护的建议.

古塔变形；各层中心点；倾斜度；弯曲度；扭曲度；变形预测

1 问题（2013年全国大学生数学建模竞赛C题）

由于长时间承受自重、气温、风力等各种作用，偶然还要受地震、飓风的影响，古塔会产生各种变形，诸如倾斜、弯曲、扭曲等。为保护古塔，文物部门需适时对古塔进行观测，了解各种变形量，以制定必要的保护措施.

某古塔已有上千年历史，是我国重点保护文物.管理部门委托测绘公司先后于1986年7月、1996年8月、2009年3月和2011年3月对该塔进行了4次观测.

请你们根据附件1提供的4次观测数据，讨论以下问题：

（1）给出确定古塔各层中心位置的通用方法，并列表给出各次测量的古塔各层中心坐标.

（2）分析该塔倾斜、弯曲、扭曲等变形情况.

（3）分析该塔的变形趋势.

2 模型假设

(1)假设附件1中的数据是以同样的方式对同样的8个点进行了4次观测.

(2)假设古塔最初建筑时是正八边形，而它的中心就是重心.

(3)假设塔尖就是一个点.

(4)假设底层不考虑弯曲和扭曲程度.

(5)假设各层的倾斜、弯曲和扭曲均是以第1层为基础作比较.

(6)假设古塔是公元1000年修建.

(7)假设古塔的变形不受强烈地质灾害影响.

3 模型建立与求解

3.1 问题1的求解

（1）分析.根据附件提供的数据信息，发现所测数据为古塔各层底部角点处的空间坐标数据，经过试算，1至13层为边长相等的空间八边形，因此我们认为，古塔修建时，1至13层为水平的平面正八边形，正八边形的中心就是各顶点的重心，由于时间久远，长时间承受自重、气温、风力等各种作用，偶然还要受地震、飓风的影响，从而产生变形，各层底面已经不再是正多边形，顶点已经变化位置，但中心应该在各层底面各顶点的重心附近，因此我们先根据《图论》中的知识得出空间有限个点的中心的定义，再运用matlab软件编程在各层底部各顶点的重心附近搜寻中心位置.

（2）空间个n点Ai(i=1,2,…,n)的中心O的定义.若空间一点O满足min﹛ max﹛ OAi﹜﹜(i=1,2,…,n)，则O叫做空间n个点Ai(i=1,2,…,n)的中心.即对空间上的任一点到这n个点的距离中有一个最大值，则所有可能的最大值中那个最小的值所对应的那个点我们就把它叫做这n个点Ai(i=1,2,…,n)的中心.

（3）各层底面中心的确定.在研究各层的中心之前，我们首先对缺失的数据进行了补充.在1986年和1996年的第十三层的第5个观测点的数据都缺失了.我们将2009年和2011年该层的同一个观测点的数据差值除以年份差作为每年的变化差值，然后计算出1986年和1996年的补充数据.然后，各层底面中心应该在各层8个观测点的重心附近，所以我们先求出其重心坐标，以其为中心构造长方体型区域，在这个区域内编程搜索满足min﹛ max﹛ OAi﹜﹜(i=1,2,…,n)的点O，其程序见附录1，计算结果如下（表1）：

表1 各年所测古塔各层中心坐标

我们运用matlab软件的三维作图工具作出古塔在各年所测的顶点与中心的图形，见图一.

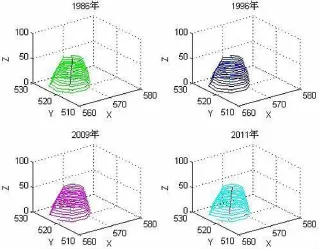
图一

3.2 问题2的求解

（1）古塔倾斜角的计算.我们认为，古塔的倾斜分为塔基的倾斜与第i层的倾斜，而倾斜度的刻画分为与铅直方向的偏离角度和偏向水平面的具体方位，这个方位我们用塔身向量在平面上的投影与轴的正方向的夹角来确定.底层倾斜角的计算我们采用将底层各顶点拟合的平面的法向量与铅直方向的偏离角度和偏向水平面的具体方位来确定，第i层的倾斜程度我们用第1层的中心为起点，第i层的中心为终点的向量与铅直方向的偏离角度和偏向水平面的具体方位来刻画.（见下图）

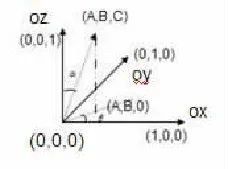
1）第一层底面（塔基）的倾斜度

我们先求出各顶点的拟合平面，设拟合平面方程为Axil+Byil+Czil=1(C＞0)，代入八个顶点坐标得到八个关于A,B,C的一次方程，然后用matlab软件解超定方程的矩阵左除法得到拟合平面的法向量（程序见附录3），m=﹛A,B,﹜C得到它与铅直方向向量{0，0,1}的夹角度数

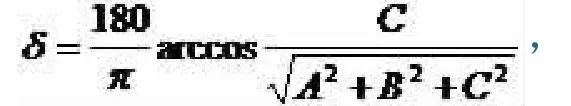
在水平面上偏离ox轴的正方向的夹角为

2）古塔第1层至第j层的倾斜度的计算

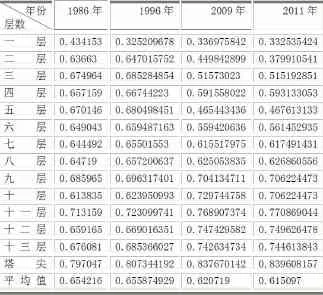
表2 各年竖直倾斜度α

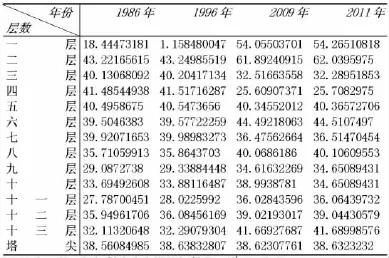
表3 各年水平偏转度θ

我们取各层的平均倾斜度为古塔的倾斜度，结果见上表.

（2）古塔扭曲度的计算.我们在每层塔的测量数据中选定第一个观测点与该层的中心点连线成一个空间向量，然后将古塔第j-1层与第j层两层的这两个向量的夹角作为古塔第j-1层的局部扭曲度，运用表2数据我们得到如下结果，见表4.

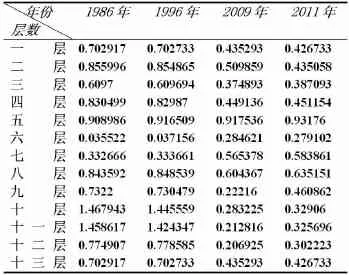
表4 扭曲度

1986年最大扭曲度在第十层，扭曲度为1.467943度，1996年最大扭曲度在第十层，扭曲度为1.445559度，2009年最大扭曲度在第五层，扭曲度为0.917536度，2011年最大扭曲在第五层，扭曲度为0.93176度.

（3）古塔弯曲度的计算.古塔在第j层的弯曲度，我们认为是由Oj-1,Oj,Oj+1这三个点确定。这三个点可确定一个圆，把这个圆的半径的倒数作为古塔在第j层的弯曲度.

接下来我们计算弯曲度，我们以第1,2,3层为例：

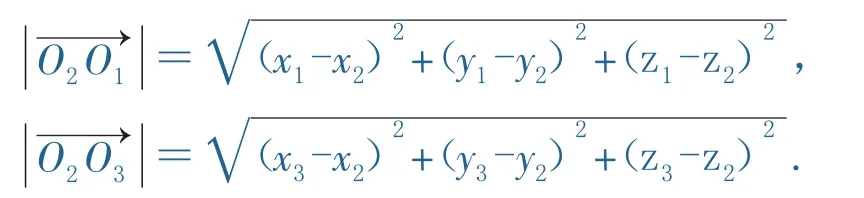
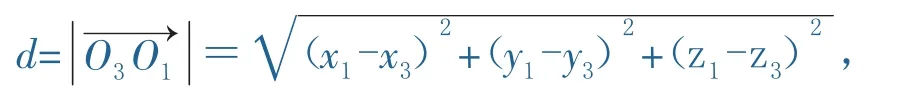
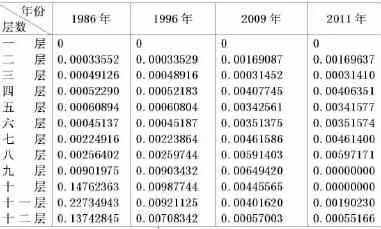
表5 各年弯曲度对比表

1986年、1996年、2009年、2011年最大扭曲分别发生在第11层、第10层、第9层、第8层，弯曲度为分别为：

3.3 问题3的求解

古塔变形趋势的预测我们假设古塔建于公元1000年，其倾斜度，扭曲度、弯曲度均为0，我们以时间t为变量，建立第t年古塔最大倾斜度，最大扭曲度、最大弯曲度的函数f(t),g(t),h(t).

首先，取古塔每年最大竖直及水平偏转度，建立了表6，再用这5个点进行回归，，通过回归方法求出倾斜函数f(t)，然后根据此函数计算，得出2011——2026年预测数据见表7，作出相应的图形，见图二、图三.

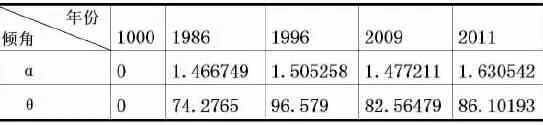
表6

倾斜函数：

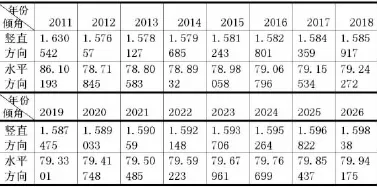
表7

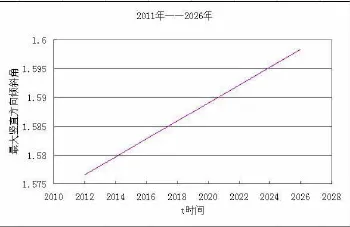
图二

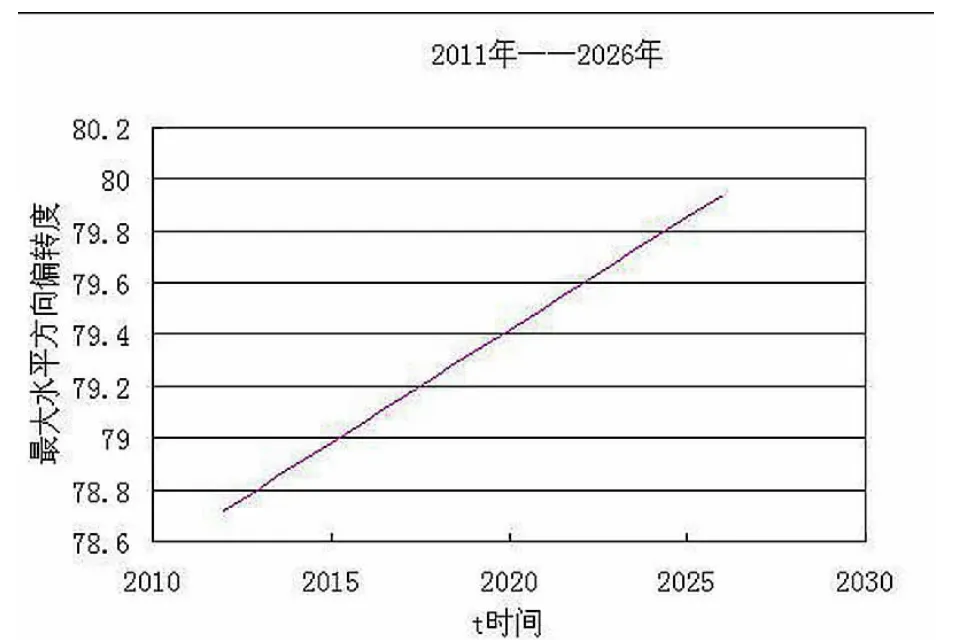
图三

取古塔每年最大扭曲度建立了表8，利用这5个点进行回归分析，通过回归方法求出扭曲函数，即最大扭曲度函数：，然后根据函数计算，得出2012——2026年预测数据见表9，作出相应的图形，见图四.

表8

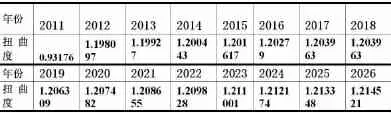
表9

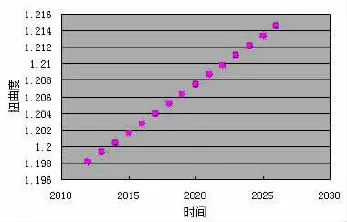
图四

表10

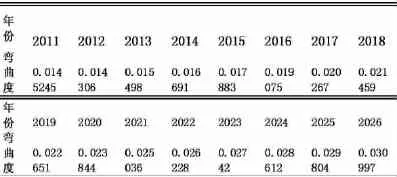
表11

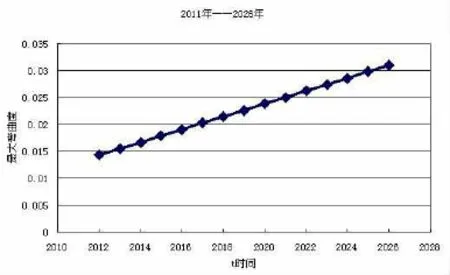
图五

4 模型评价与改进

本文在实际问题的基础上，通过合理的假设，预测出古塔的最大可能的倾倒方向，可以协助有关部门对古迹的维护.

充分利用excle来对大量的数据进行计算，完成表格的输入、统计、分析等多项工作，可生成精美直观的表格、图表.

Matlab是一种科学计算软件，专门以矩阵的形式处理数据，利用matlab计算可以使我们所计算的数据更加精确.

[1]陈国华,韦程东.数学建模与数学建模方法[M].天津：南开大学出版社，2012.

[2]陈光亭,裘哲勇.数学建模[M].北京：高等教育出版社，2012.

[3]梁海奎.古塔变形测量方法探讨[J].城市勘测，2011，（3）.

[4]吴望名.图论及其应用[M].北京：科学出版社，1984.

责任编辑：张隆辉

O 29

A

1672-2094(2013)06-0155-05

2013-10-28

唐纪芳（1982-），女，四川遂宁人，四川职业技术学院应用数学与经济系讲师，硕士。

张子卫（1963-），男，四川遂宁人，四川职业技术学院应用数学与经济系副教授。