小波分析在测井数据融合处理中的应用

雷芬丽，许 平，程武伟，黄世强

（浙江华东工程安全技术有限公司，杭州 310014）

小波分析在测井数据融合处理中的应用

雷芬丽，许 平，程武伟，黄世强

（浙江华东工程安全技术有限公司，杭州 310014）

受各种干扰和人为因素影响，单一的地球物理测井信号曲线存在多解性和局限性。本文综合利用多条测井信号所反映的地层信息，应用小波分析方法，采用多尺度分析理论重构小波变换系数模极值，从而将多条测井曲线信号融合成一条参数曲线。通过对融合后的参数曲线解译，增强了原始测井曲线中所包含的共有信息，削弱了单条测井信号中存在的偶然误差，使测井数据的可信度大为提高。阐述了数据融合处理的原理与具体方法，并结合工程实际分析了应用实效。该方法有助于更好地分析和解决实际工程问题。

地球物理探测；测井技术；数据融合；测井曲线；小波分析；多尺度分析

地球物理测井技术是解决矿产资源地质、工程地质、灾害地质、生态环境等问题的重要手段[1]。地球物理测井是一门仍在迅速发展的技术学科，特别是20世纪90年代后，测井技术取得长足发展，应用领域也在不断扩展[2～7]。

测井技术是对钻井内实际地质情况的间接反映，必须将测井信息进行处理和加工，才能达到分析和解决问题的目的。由于受到各种干扰因素和人为因素的影响，分析单条测井信号曲线得出的结论往往存在多解性和局限性。为此，本文提出应用小波多尺度分析方法融合处理多条测井信号成一条测井参数曲线，以增强原始测井曲线的公共信息，削弱单一测井信号中的偶然误差，从而提高测井资料的可信度和分析解决实际工程问题的能力与水平。

1 小波系数模极值多尺度重构

岩性、地层结构等各种地质信息综合反映在测井曲线上，当测量工作是在传统单一尺度上进行并从测井信号中提取各类信息，各种噪声信号往往会将测量有效信号淹没。小波变换的多尺度分析方法很大程度上弥补了传统信号分析的弱点，并在实际资料处理中得到了很好的应用效果，即测井信号采用小波变换在多个尺度上分解，使噪音减弱，测量信号的信噪比得到大大提高，对原始测量信号小波多尺度分析可取得比单一尺度更好的处理效果。

作为小波分析核心内容的多尺度分析形成于20世纪80年代后期，在1990年美国电气和电子工程师协会（IEEE）第29届IEEE控制与决策会议上，美国学者A. Benveniste、R. Nikoukhah和A. S. Willsky提出了多尺度分析理论的框架体系[8]，之后其在控制系统、地球物理勘探、信号处理等领域中得到了广泛应用[9～13]。

实际测井资料处理过程中，一个关键的问题是小波变换系数模极值能否完全包含整个测井信号，即能够根据小波系数模极值的信息重构测井曲线。为快速计算小波系数，考虑二进离散尺度上的小波变换系数模极值，S. G. Mallat最先研究该问题[14]，提出交替投影算法，在一定约束条件下可重构出与原始信号十分逼近的信号[15]。

交替投影算法运用平方可积函数F(x)在多个尺度下的小波变换函数W2jF(x)的局部极值及位置求信号的估计函数为极大值位置序列由小到大排列）。

交替投影法的基本思想是：

（2）对每一个j，求函数G(x)使W2jG(x)=gj(x)并尽可能等于hj(x)。

求 G(x)采用迭代法，取初始值G(x)=0，所以对于每一个j，gj(x)=0。设εj(x)=hj(x)-gj(x)，而当gj(x)为已知时，求hj(x)转化成求εj(x)。

εj(x)满足：

其Euler方程为：

求得Euler方程的通解： ，由边界条件（3）式确定α、β。将通解代入εj(x)=hj(x)-gj(x)后得到{hj(x)}。

最后求函数G(x)：设平方可积函数γ(x)的二进小波集合为{yj(x)| j∈Z}，记W(γ(x))={yj(x) | j∈Z}，于是根据小波变换W及逆变换W-1的关系有：

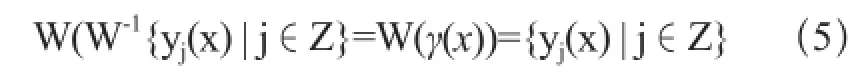
说明二进小波变换集合{yj(x) | j∈Z}在WW-1的作用下不变。令G'(x)=W-1{gj(x)| j∈Z}。以初值{gj(x)=0 | j∈Z}的改进值作为新初值，按上述迭代方法可以算出进一步改进值

2 测井资料多尺度融合

基于模极值边缘检测的数据融合是分别对各条测井信号曲线进行二进小波分解，找出各尺度上模极大值点，比较不同尺度下各测井曲线小波分解后在同一尺度上的细节信息，提取重要的小波变换系数[16]，最后就不同尺度进行小波逆变换[17]，可得到小波分析多尺度数据融合后的综合测井参数曲线。

下面以两条测井曲线为例，多尺度数据融合的基本步骤是：

（1）分别对两条测井曲线进行趋势分析预处理；

（2）测井曲线的归一化处理；

（3）设分解层次为J，对归一化测井信号进行二进小波变换，找出各尺度下模极值点。

（4）将测井曲线的小波变换系数模极大值在各个尺度j (j=1，2，…，J)上进行比较，保留各尺度上对应位置高频系数模极大值较大的小波系数，即

其中，和分别表示在j尺度下两条测井曲线信号对应点的高频系数值；

（5）对测井信号进行小波分解后的逼近系数cA1J和cA2J处理：与信号的细节信息相比，曲线低频信息保持较好，因此两条测井曲线经小波分解后其模极值的差异要远大于逼近系数之间差异，故数据融合后逼近系数可由下式确定：

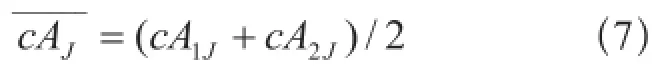
另，依据两条测井曲线的实际情况，(7)式可进一步推广为：

式中：α+β=1。

3 实际资料处理

根据上述讨论方法，现对某实际工程中钻井测试得到的自然伽马（GR）曲线和自然电位（SP）曲线进行小波多尺度数据融合，图1表示GR、SP测井曲线多尺度融合得到测井参数曲线的过程。图2(a)、(b)分别表示GR曲线和SP曲线归一化值，图2(c)表示多尺度融合后的测井参数曲线，从曲线图中可以看出，数据融合后测井参数曲线突显了两条测井曲线的公共部分，削弱了原始测井信号中个别畸变点的局部影响。比较三条测井参数曲线的小波系数色谱图，如图3所示，(a)中红色线框区域内能量团是因GR曲线的突变引起，(c)中融合测井参数曲线小波色谱图上红框区域内能量团得到相应减弱；(a)、(b)中黑色线框区域内能量团共同反映了相应的地质公共信息，(c)中融合后测井参数曲线小波系数色谱图黑框区域能量团也较强，证明融合测井曲线突出了多条测井曲线的公共信息。

图1 两条测井曲线的融合过程Fig.1 Fusion processing of two well logging curves

图2 测井曲线归一化及融合Fig.2 Normalization and fusion of logging curve

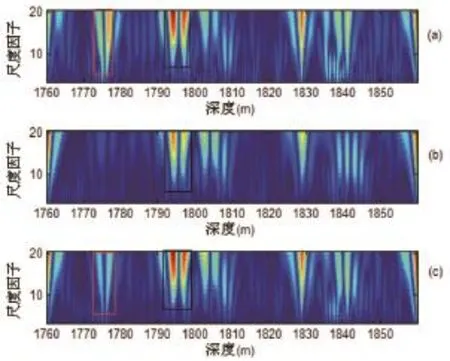
图3 小波系数色谱图Fig.3 Wavelet coefficients chromatogram

4 结论

（1）依据小波多尺度分析理论，对曲线信号进行多尺度分析，把一维的测井信号变换到二维的时间—尺度（频率）域，清晰展示出信号内部的能量聚集与分布，从而在复杂多变的原始测井信号中提取出测井数据所不能体现的信息。

（2）以模极大值重构算法和小波多尺度边缘检测方法为基础，利用测井信号多尺度分析的高频系数取模极大、低频系数加权的融合规则，进而融合处理多条测井曲线信号成一条参数曲线。小波多尺度分析融合后的测井参数曲线增强了原始测井曲线的公共信息，减弱了单一测井信号中存在的偶然误差，提高了测井资料的可信度。

References)

[1]中国科学院士刘光鼎教授接受本刊专访. 地质调查深化拓展应重视地球物理学[J]. 上海国土资源,2013,34(1):1-4.

Liu G D. Geological survey deepening development should attach importance to the geophysics[J].Shanghai Land & Resources, 2013,34(1):1-4.

[2]杨建刚. 工程物探方法在上海城市建设与管理中的应用[J]. 上海地质,2006,27(4):14-18.

Yang J G. The application of engineering-physical geography on city construction and management in Shanghai[J].Shanghai Geology,2006,27(4):14-18.

[3]许方伟,陆次平,王荷萍,等. 用测井信息综合评价钻遇地层[J]. 上海地质,2004,25(2):48-53.

Xu F W, Lu C P, Wang H P, et al. Using logging data to evaluate the drilling strata compositely[J].Shanghai Geology,2004,25(2):48-53.

[4]王治华,杨建刚. 物探在上海地区工程性地质灾害勘查中的应用分析[J]. 上海地质,2009,30(4):12-16.

Wang Z H, Yang J G. The application analysis of geophysical exploration for the geological disaster survey in Shanghai[J].Shanghai Geology,2009,30(4):12-16.

[5]张舒杰,吴健生,赵永辉,等. 综合物探方法在城市地下桩基地籍调查中的应用研究[J]. 上海国土资源, 2012,33(4):80-83,88.

Zhang S J, Wu J S, Zhao Y H, et al. Application of integrated geophysical methods to urban underground pile foundation cadastral investigate[J].Shanghai Land & Resources, 2012,33(4):80-83,88.

[6]司永峰,王永. 基于重力场和磁场测量的地下管道三维探测研究[J]. 上海国土资源,2013,34(1):76-80.

Si Y F, Wang Y. 3D detection of underground pipelines using magnetic and gravity field measurements[J].Shanghai Land & Resources,2013,34(1):76-80.

[7]刘伍,曾来,司永峰,等. 地下障碍物探测井中地震散射波成像数值模拟[J]. 上海国土资源,2012,33(3):66-70.

Liu W, Zeng L, Si Y F, et al. Numerical simulation of borehole seismic scattered wave imaging for the detection of underground obstacles[J].Shanghai Land & Resources, 2012,33(3):66-70.

[8]Benveniste A, Nikoukhah R, Willsky A S. Multiscale system theory[A]. Proceedings of the 29th IEEE Conference on Decision and Control[C], 1990:2484-2487.

[9]赵巍,潘泉,戴冠中,等. 多尺度系统理论研究概况[J]. 电子与信息学报,2001,23(12):1427-1433.

Zhao W, Pan Q, Dai G Z, et al. Development of multiscale system theory[J].Journal of Electronics and Information Technology, 2001,23(12):1427-1433.

[10]房文静,范宜仁,李霞. 多尺度分析方法及其在测井中的应用[J].测井技术,2006,(2): 139-141,194.

Fang W J, Fan Y R, Li X. Multiscale Analysis and Its Application in Well Logging[J].Well Logging Technology,2006,(2): 139-141,194.

[11]房文静,范宜仁,李霞. Morlet小波用于测井沉积旋回多尺度特性研究[J]．物探化探计算技术,2007,2(2):109-111.

Fang W J, Fan Y R, Li X. The multi-scale characteristic study of sedimentary cycle in well logging data using morlet wavelet[J].Computing Techniques for Geophysical and Geochemical Exploration,2007,2(2):109-111.

[12]李霞,范宜仁,房文静,等. 测井多尺度分析方法用于层序地层划分研究[J]. 新疆地质,2006,24(4):454-457.

Li X, Fan Y R, Fang W J, et al. Research on the demarcation sequence stratigraphy using multiscale analysis method of well logging[J].Xinjiang Geology,2006,24(4):454-457.

[13]许平. KJZ盆地新近系地层测井参数分析及应用[D]. 成都理工大学硕士学位论文,2011.

Xu P. Analysis and application of logging parameters in Neogene layer of KJZ basin[D]. Master's thesis, Chengdu University of Technology, 2011.

[14]Mallat S G. Multiresolution approximation and wavelet orthonormal bases[J].Transactions of the American Mathematical Society,1989,315(1):69-88.

[15]于继锋,李增学. 测井数据小波变换及其地质意义[J]. 中国矿业大学学报,2003,32(3):336-339.

Yu J F, Li Z X. Wavelet transform of logging data and its geological significance[J].Journal of China University of Mining & Technology,2003,32(3):336-339.

[16]陈正星. 小波分析算法与应用[M]. 西安:西安交通大学出版社, 1998.

Chen Z X. Wavelet analysis algorithms and its applications[M]. Xi’an: Xi'an Jiaotong University Press,1998.

[17]李红波. 基于融合算法的沉降监测数据反馈分析[J]. 上海国土资源,2013,34(2):84-87.

Li H B. Feedback analysis of subsidence monitoring based on data fusion algorithm[J].Shanghai Land & Resources,2013,34(2):84-87.

Application of wavelet analysis for multi-scale fusion of well logging data

LEI Fen-Li, XU Ping, CHENG Wu-Wei, HUANG Shi-Qiang
(Zhejiang Huadong Engineering Safety Technology Co., Ltd., Hangzhou 310014, China)

Using a single well-logging curve can help to solve practical engineering problems. However, the results often have multiple solutions and limitations due to various interfering and human factors. The fusing of multiple logging curves into a new parameter curve using wavelet multi-scale analysis can facilitate the utilization of multiple logging curves that contain useful information. Based on the theory of signal detection and multi-scale analysis, publicly available information contained in the original curves is enhanced, the accidental error associated with single well data has been reduced, and the credibility of the comprehensive well logging dataset has been improved.

geophysical prospecting; well logging technology; fusion of data; well logging curve; wavelet analysis; multiscale analysis

P631.8

A

2095-1329(2013)04-0087-04

10.3969/j.issn.2095-1329.2013.04.020

2013-09-27

2013-10-30

雷芬丽(1983-),女,工程师,主要从事地球物理勘探技术研究.

电子邮箱：lei_fl@ecidi.com

联系电话：0571-56553775