面向等几何分析的B样条参数体生成方法

许华强， 徐 岗， 胡维华， 汪国昭

（1. 杭州电子科技大学计算机学院图形图像研究所，浙江 杭州 310018；2. 浙江大学数学系图像图形研究所，浙江 杭州 310027）

随着CAD/CAE 领域的快速发展和降低设计成本的需要，设计与分析的一体化已成为大势所趋[1]。目前，有限元分析已经成为CAE 领域对CAD 产品进行仿真模拟的主流方法。然而，当今设计与模拟分析阶段几何数据模型的不一致性，严重影响了求解精度和计算效率。据统计，数据交换可以占到CAE 软件大约70%的运行时间，而整个CAD/CAE 过程80%左右的工作量用于离散网格生成阶段。此外，由于有限元分析中的计算域只是对CAD模型的逼近表示，这必然导致模拟分析及优化结果存在一定的误差。对于某些模拟仿真中的物理问题而言，由此所导致的误差可能会非常显著，因此，如何实现真正意义上的CAD/CAE 系统的无缝融合，便成为CAD/CAE 向前发展过程中亟需解决的问题。

等几何分析方法的提出为实现CAD/CAE系统的无缝融合提供了新途径[2]。相对于经典的有限元分析方法，该方法的主要优势在于：

1）具有与CAD阶段统一的几何数学模型，或者两个阶段的几何数学模型具有互用性，无需进行容错转换；

2）采用高阶基函数作为形函数，具有良好的收敛性；

3）求解所得到的物理场具有高阶连续性，对某些薄壳问题的求解可达到比较高的精度；

4）实现了CAD 模型与计算域的精确转换，提高了模拟分析及优化设计的准确度；

5）在细化过程中（节点插入或升阶操作）可以使计算域的几何保持不变[3]，这一特性适用于流体和固体的耦合问题。等几何分析方法的提出为已趋成熟的几何造型领域注入了新的活力，目前已成为几何设计与计算领域新的关注热点，由于等几何样条分析的研究目前处于起步阶段，该方法在应用的广度与模拟的自适应性等方面仍存在一定的局限性。

等几何分析方法虽然无须由CAD 模型的边界曲面表示生成离散的四面体网格作为计算域，但仍然需要由其边界表示生成连续的参数样条体表示以完成计算域的构造。这一体参数化过程与有限元方法中的网格生成过程的不同之处在于：我们需要在精确保持边界曲面的前提下，将CAD 模型的内部用若干个三变量参数体填充起来，而有限元分析中的网格生成过程得到的则是该CAD模型的四面体网格逼近表示。CAD 模型的体参数化结果对模拟分析的精度有着重要影响[4]，这一问题在Cottrell 和 Hughes 等所著的《Isogeometric Analysis: Toward Integration of CAD and FEA》一书中被列为等几何分析面临的最富有挑战性的公开问题之一。目前，国际上对这一问题的研究屈指可数。Martin 等利用离散调和函数方法来完成对四面体网格的参数体逼近[5]；Escobar 等利用参数域剖分和插值逼近技术来构造三角网格模型的三变量T 样条体参数化[6]；Zhang 等利用参数映射和八叉树技术来构造三角网格模型的三变量T样条体参数化[7]。上述3种方法虽然均可有效生成体参数化，但它们的缺点是显而易见的，即其输入是三角网格模型或者四面体网格模型，而参数样条表示是CAD系统中的标准形式，显然违背了等几何分析方法的精髓——精确几何表示。理想的方法应该是以CAD 模型的边界样条曲面表示作为输入，构造其内部空间的参数体表示。本文提出了基于模板的由边界曲面生成参数体的新方法。首先给出了插值边界曲面的Coons体的参数表达式。由该表达式的离散表示，内部控制顶点可表为边界控制顶点的线性组合。然后由其离散表示可得到Coons模板，并将Coons模板推广到统一形式，这为内部控制顶点的生成提供了更多选择。本文通过几个热传导问题的例子对由不同的模版所得到的不同的体参数化结果及其对等几何分析结果的影响进行了比较分析。

1 Coons 参数体

给定6张边界曲面S(0,v,w),S(1,v,w) ,S(u,0,w),S(u, 1,w),S(u,v, 0),S(u,v, 1), 插值上述6张曲面的Coons参数体S(u,v,w)可按如下方式构造：

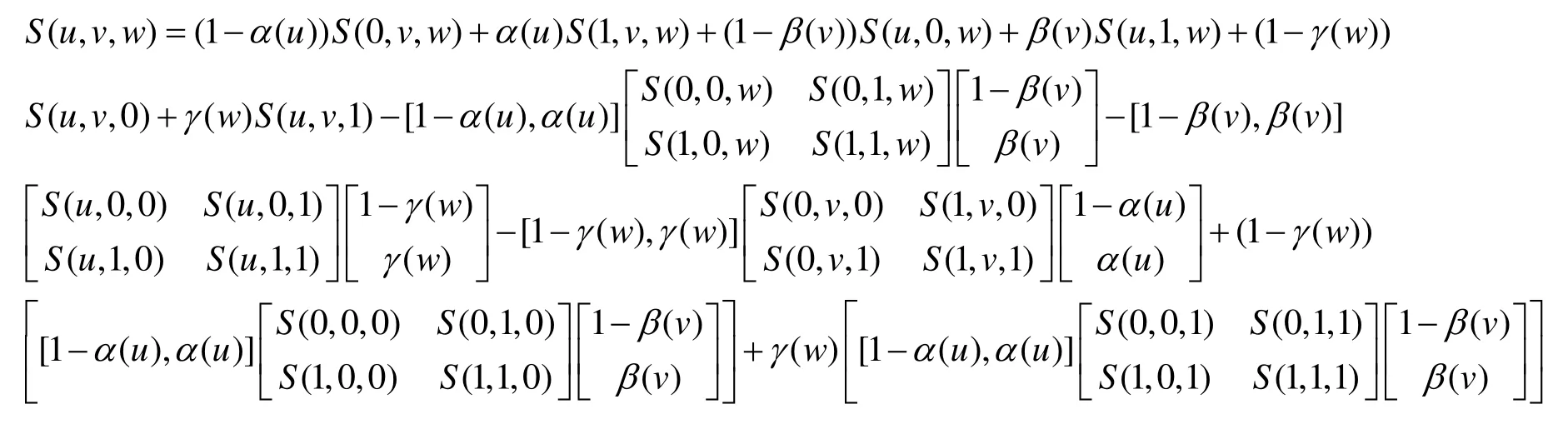
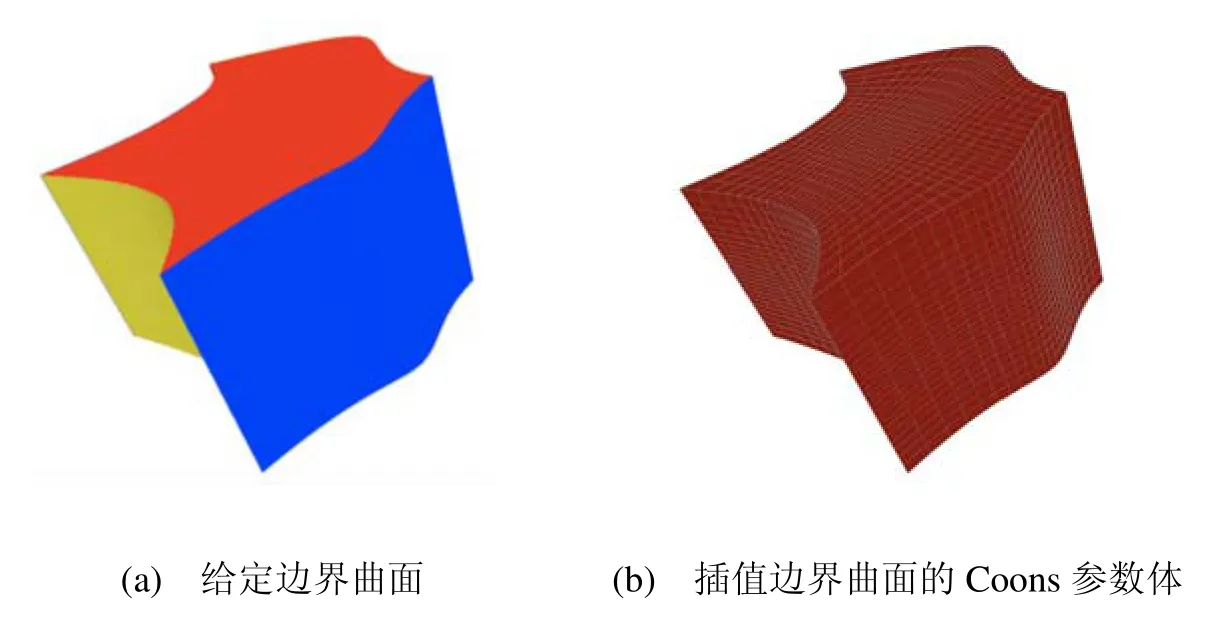
图1 Coons参数体

其中，α(u)β(v)γ(w)为满足如下条件的参数函数：

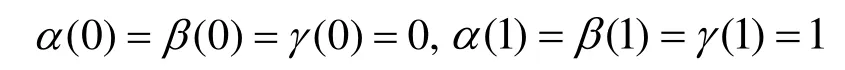
通过直接计算可证明参数体S(u,v,w)插值6张边界参数曲面，它可以看作插值4条边界曲线的Coons曲面的推广。图1给出了一个Coons参数体S(u,v,w)的例子。

若给定的边界曲面为B样条曲面，并且相对的B样条曲面具有相同的次数、控制顶点数目和节点向量，α(u)β(v)γ(w)为参数多项式函数，则按照Coons 参数体的定义所生成的参数体仍为B样条形式。若α(u) =u,β(v)=v，γ(w) =w,并且边界控制顶点按图2给出，则每一个控制顶点Pi,j,k可赋予一组参数值(u,v,w) =(i/l,j/m,k/n)， 内部的控制顶点Pi,j,k可按照如下的离散形式构造：

则相应的B样条参数体可记为

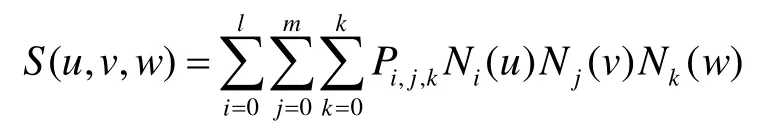
其中，Ni(u),Nj(v),Nk(w)为B样条基函数，其节点向量由边界B样条曲面给出。

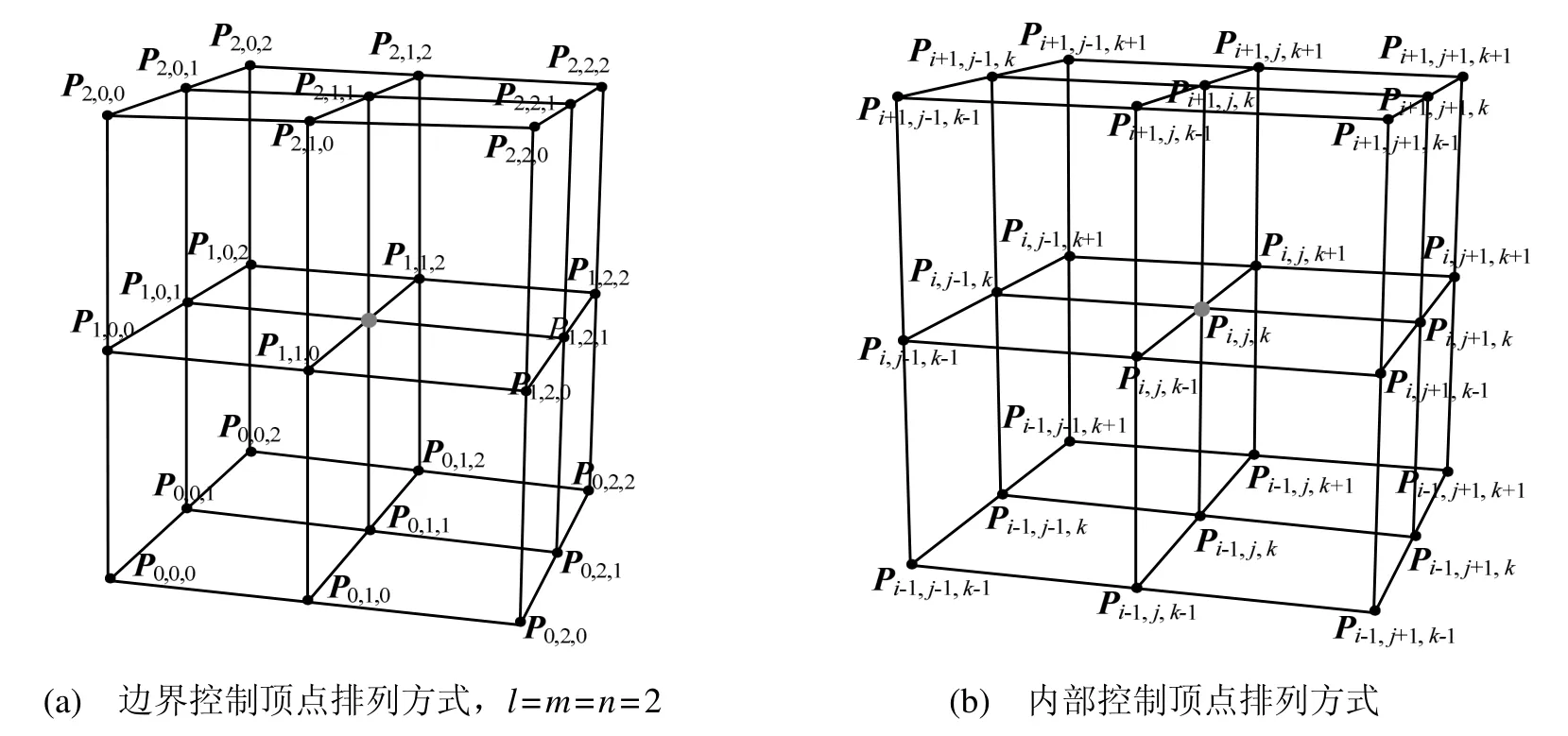
图2 排列方式

2 B样条参数体生成的模板方法

本文所提出的模板实际上表达了每一个内部控制顶点与其相邻控制顶点的线性关系。对B样条Coons体的每一个内部控制顶点Pi,j,k来说，其与相邻控制顶点之间的关系可表示为

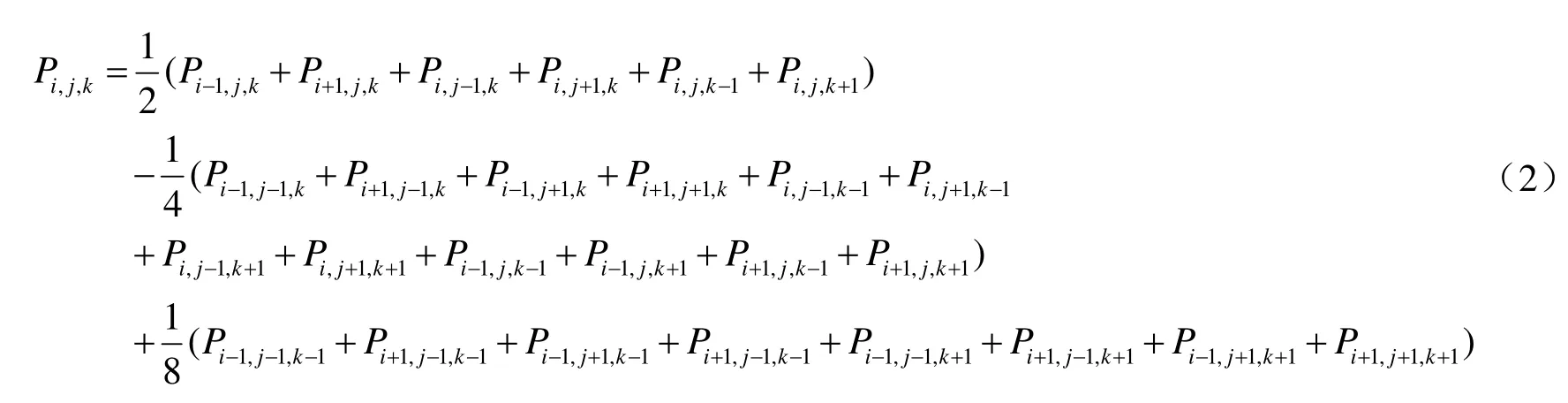
上述关系可以表示为图3(a)中简洁的模板表示。对一个具有(l-1)× (m-1)× (n-1)个内部控制顶点的B样条参数体来说，我们将得到(l- 1)× (m-1)× (n -1 )个线性方程。其所组成的线性系统的系数矩阵为一稀疏矩阵。在B样条体的内部，其表现为内部待求控制顶点之间的关系，而在其边界，则表现为边界已知控制顶点与内部待求控制顶点之间的关系。

等式(2)所表示的离散Coons模板可以扩展到如下形式：

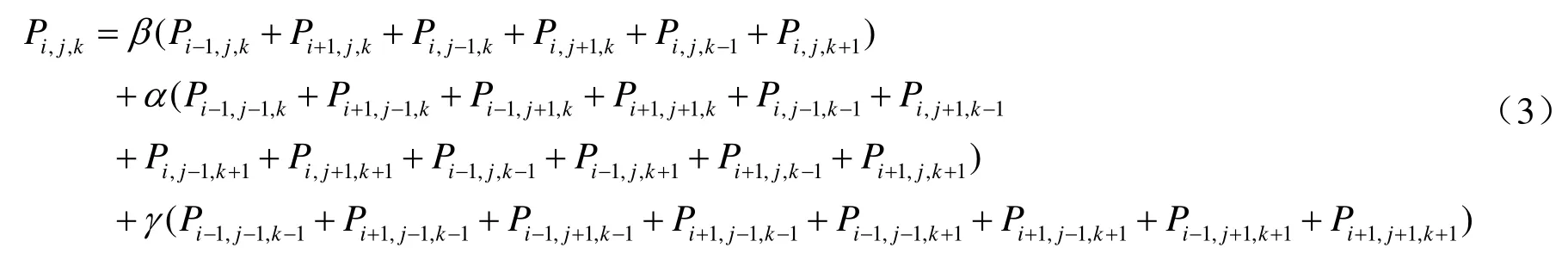
上述关系可以表示为图3(b)中简洁的模板表示。该模板表示方法提供了3个参数α,,βγ，增加了B样条参数体生成的自由度。为使内部待求的控制顶点位于边界已知的控制顶点所组成的凸包内，参数α,,βγ应满足如下约束条件

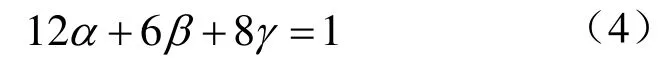
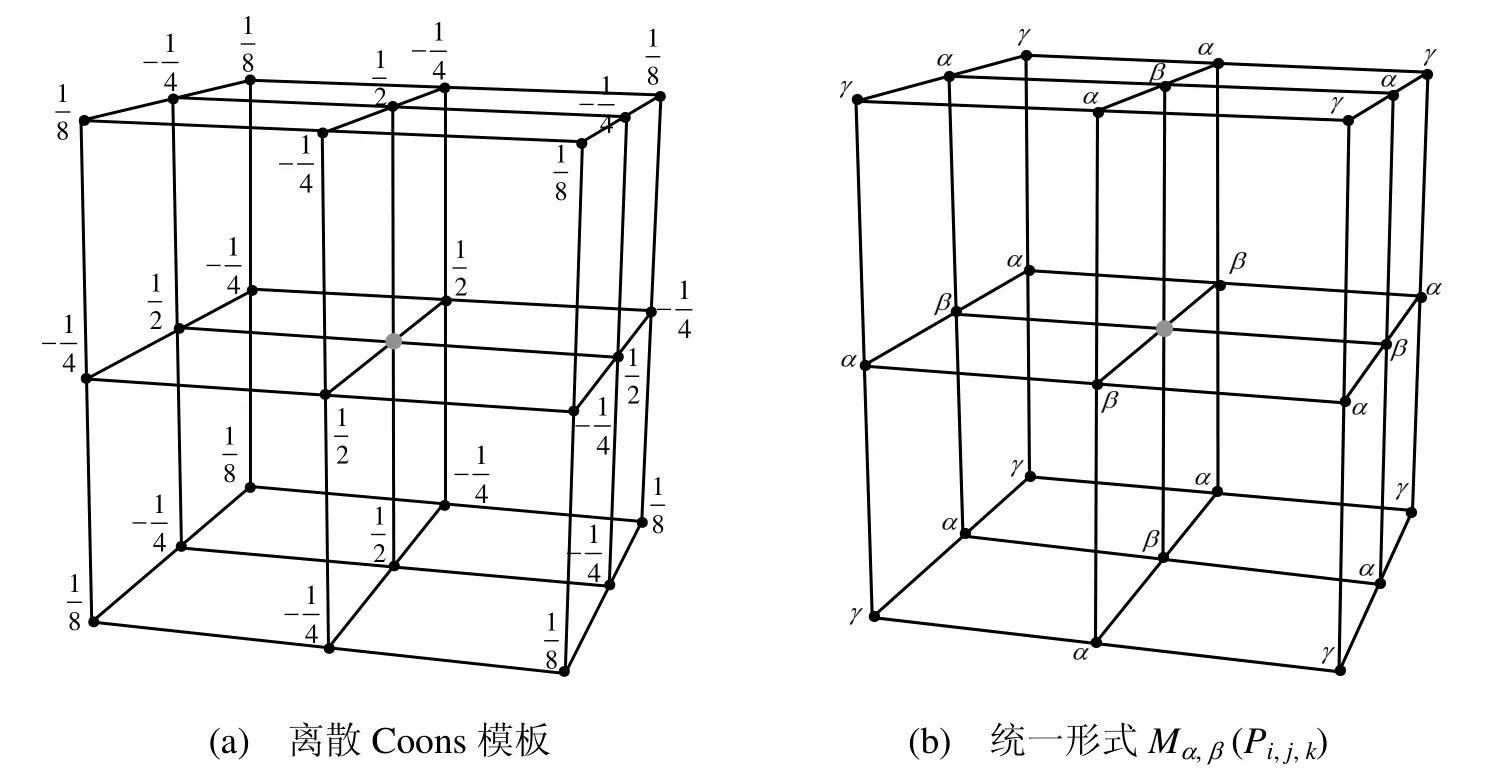
图3 模板表示方法

该模板表示形式可以记为Mα,β(Pi,j,k)。对于给定的边界B样条曲面，用户可选择不同的参数α,β来构造B样条参数体，γ可根据α,β的值由式（4）求出。例如，离散Coons模板可记为其中离散Laplacian 模板可记为，其中离散调和模板可记为其中

图4给出了在边界B样条曲面相同的情形下，依据上述3种不同的模板方法所生成的B样条参数体的例子。为将3种模板进行比较，本文给出了所生成的B样条参数体的等参数曲面分布，可以发现离散调和模板所生成的B样条参数体的等参数曲面分布最为均匀。另外，本文将生成的体参数化结果在三维等几何分析中进行了测试。所求解的物理仿真问题为如下的三维热传导问题：

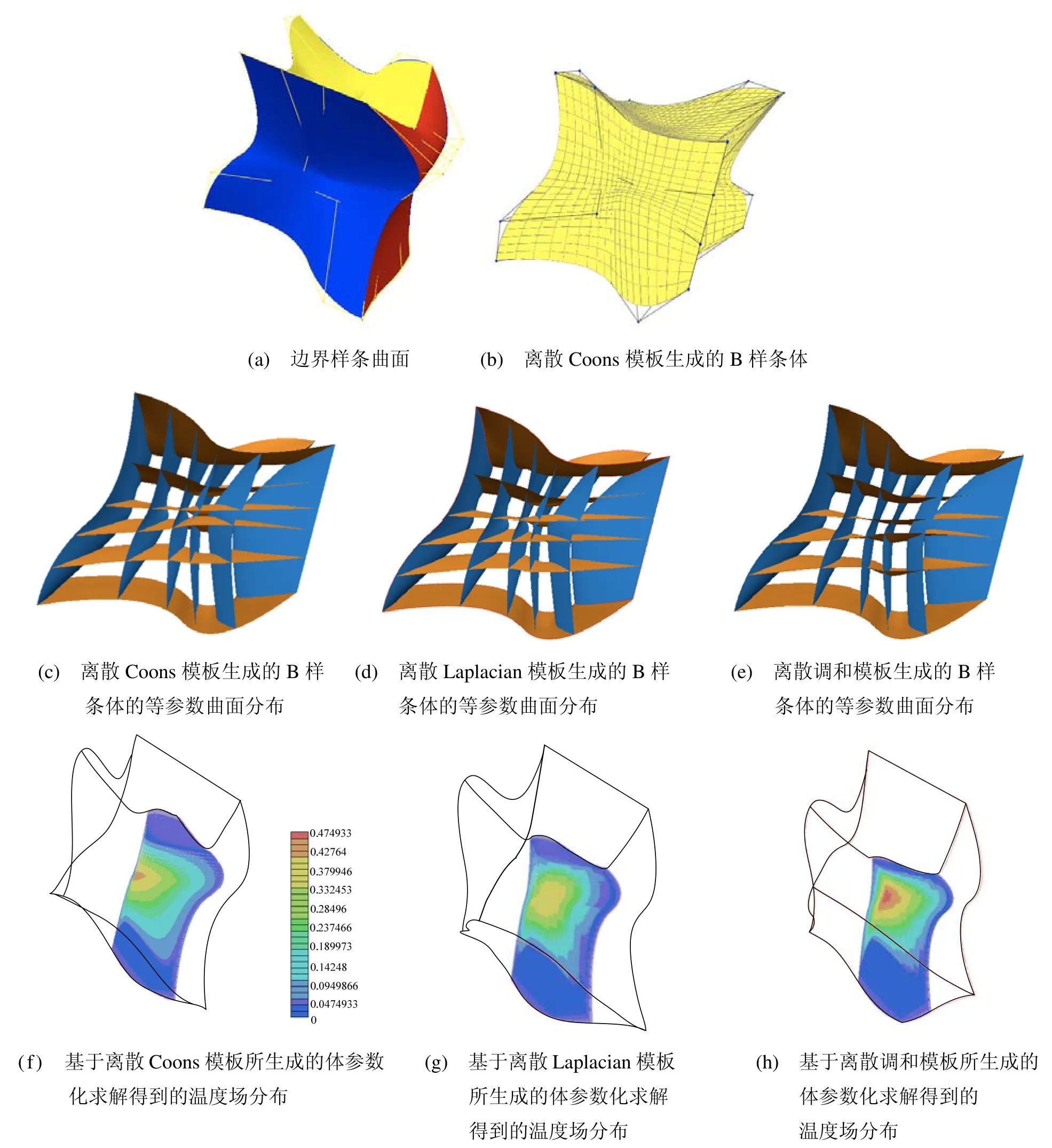
图4 体参数化实例

3 结 论

三维等几何分析中的计算域通常表示为参数样条体。本文提出了一种由边界曲面生成参数体的模板方法。首先给出了插值边界参数曲面的Coons体的参数表达式。由其离散表示可得到Coons模板，并将Coons模板推广到统一形式，这为内部控制顶点的生成提供了更多自由度。通过模板方法，内部控制顶点可通过求解一个稀疏线性系统得到。本文通过热传导问题的实例对由不同的模板所得到的体参数化结果及其对等几何分析的影响进行了比较分析。

[1]高曙明, 何发智. 异构CAD系统集成技术综述[J]. 计算机辅助设计与图形学学报, 2009, 21(5): 561-568.

[2]Hughes T J R, Cottrell J A, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry, and mesh refinement [J]. Computer Methods in Applied Mechanics and Engineering, 2005,194(39-41): 4135-4195.

[3]徐 岗, 王毅刚, 胡维华. 等几何分析中的r-p型细化方法[J]. 计算机辅助设计与图形学学报, 2011,(12): 2019-2024.

[4]Xu Gang, Mourrain B, Duvigneau R, et al.Parameterization of computational domain in isogeometric analysis: methods and comparison [J].Computer Methods in Applied Mechanics and Engineering, 2011, 200(23-24): 2021-2031.

[5]Martin T, Cohen E, Kirby R M. Volumetric parameterization and trivariate B-spline fitting using harmonic functions [J]. Computer Aided Geometric Design, 2009, 26(6): 648-664.

[6]Escobar J M, Cascon J M, Rodrıguez E, et al. A new approach to solid modeling with trivariate T-splines based on mesh optimization [J]. Computer Methods in Applied Mechanics and Engineering, 2000, (45-46);2011, 3210-3222.

[7]Zhang Y, Wang W, Hughes T J R. Solid T-spline Construction from boundary representations for genus-zero geometry [J]. Computer Methods in Applied Mechanics and Engineering, 2012,(249-252):185-197.