空间到Q空间的积分型算子的有界性T,s

古勇毅

（五邑大学数学与计算科学学院，广东江门 529020）

古勇毅

（五邑大学数学与计算科学学院，广东江门 529020）

对空间到QT,s空间的积分型算子为有界算子进行等价刻画.利用|f(z)|的估计讨论了空间到QT,s空间的积分型算子的有界性，并给出了空间到QT,s空间的积分型算子有界的充分必要条件.

空间；QT,s空间；积分型算子；有界性

1 相关知识

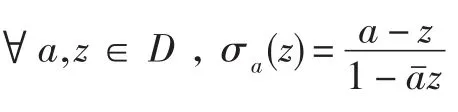
本文中C为一个正常数，且在不同地方可以表示不同的值.

定义1[1]设QT，D上的对数QK函数空间定义为

设T(r)是实的非减函数T(r):[0,∞)→[0,∞)，则

定义3[3]QT空间定义如下：

定义4[4]QT,s空间定义如下：设0＜s＜∞，

显然，QT,2=QT；若取T(r)=rp(0＜p＜+∞)，则QT=Qp；当s=2且取

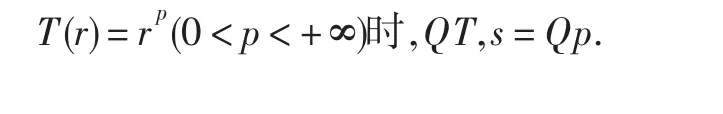
2 主要结论

引理1[5]对任意的f∈，z∈D，有

定理1设τ∈B(D)，ϕ∈H(D)，则当0＜α＜1时，JτCϕ:→QT,s有界当且仅当

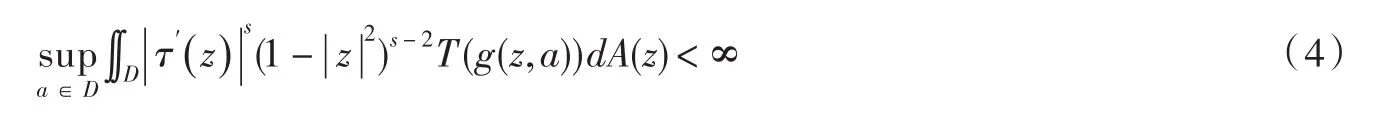
证明充分性：对任意的f∈，因为|CϕJτf(0)|=0，所以

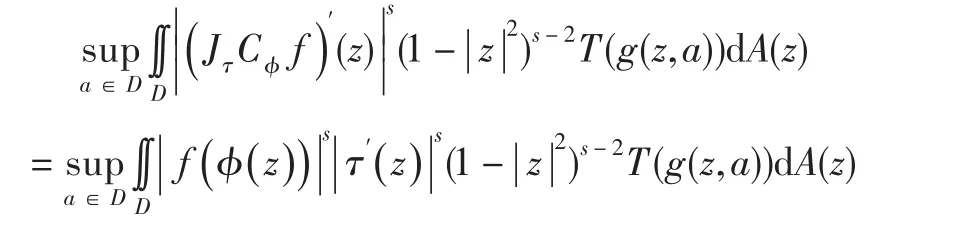
由引理1的（1）式有：

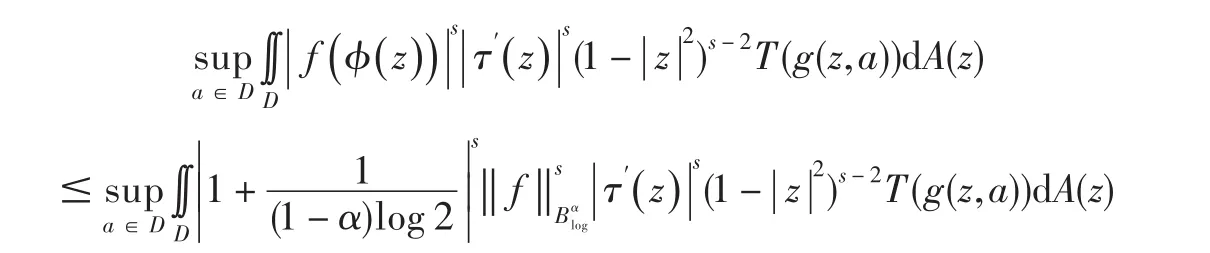
定理证毕.

定理2设τ∈B(D)，ϕ∈H(D)，则当0＜α＜1时，→QT,s有界当且仅当

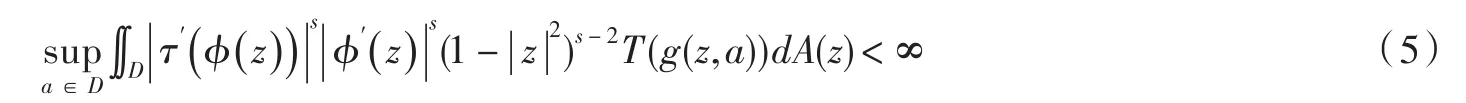
证明充分性：对任意的f∈，因为，故有

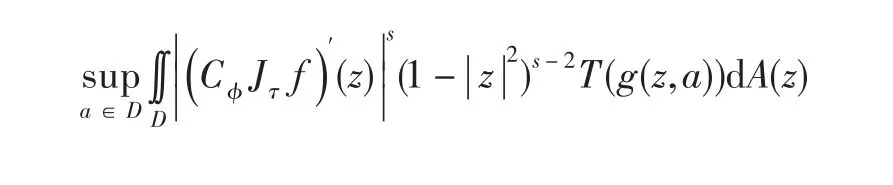
由引理1的（1）式有：

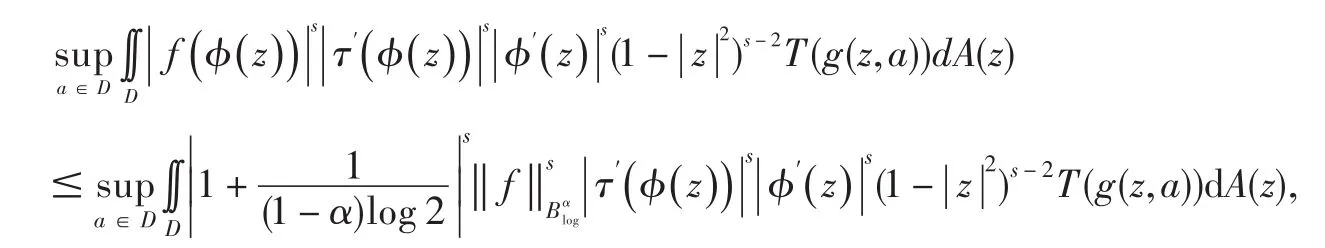
[1]Li H,Liu p.Composition operators between generally weighted Bloch space andspace[J].Banach Journal of Mathematical Analysis,2009,3(1):99-110.

[2]乌兰哈斯.Mobius不变的QP空间：结果、技巧和问题[J].数学进展，2005，34（4）：385-403.

[3]Wulan hasi,Wu pengcheng.Characterizations ofQTspaces[J].Math Anal Appl,2001,254:484-497.

[4]周江河，谭海鸥.关于解析QT,s空间[J].五邑大学学报：自然科学版，2009，23（3）：50-52.

[5]Li Haiying,Liu Peide,Wang Maofa.Composition operators between generally weighted Bloch space of polydisk[J].Inequalities in Pure and Applied Mathematics,2007,8(3):1-8.

New Character ofQT,sSpaces

GU Yong-yi
(School of Mathematics and Computational Science,Wuyi University,Jiangmen 529020,China)

In this paper,the equivalent characterizations of boundedness of integral type composition operators acting fromspaces toQT,sspaces are given.

spaces;QT,sspaces;composition operator;boundedness

O174.5；O177.2

A

1008-2794（2013）04-0017-03

2013-04-10

国家自然科学基金资助项目“复微分方程的相关研究”（11126327）

古勇毅，五邑大学数学与计算科学学院研究生，研究方向：复分析及其应用，E-mail：guyoyi05101@163.com.