扩*-亚序与实*-环
姜伟,黄冬明
(1.常熟理工学院数学与统计学院,江苏常熟 215500;2.海南大学信息科学技术学院,海南海口 570228)
扩*-亚序与实*-环
姜伟1,黄冬明2
(1.常熟理工学院数学与统计学院,江苏常熟 215500;2.海南大学信息科学技术学院,海南海口 570228)
在取定*-环的一个扩*-亚序T的基础上,研究了*-环的T-模和*-序的一些联系,刻画了*-环的实性的一个判别条件,并探讨了*-环的扩*-亚序、*-亚序和*-序的一些联系.
*-环;*-序;扩*-亚序;实代数
在本文中,R表示包含单位元1的环.R的一个变换*称作对合映射,如果满足(r+s)*=r*+s*,(rs)*=s*r*且(r*)*=r,其中r,s∈R;*-环一般表示带有对合*的非交换幺环.若有r*=r,其中r∈R,则称r是R中的对称元.我们定义S(R)={r∈R|r*=r}.一般来说,S(R)在R之中不是乘法闭子集,但是S(R)是R的一个加法子群.如果a,b∈S(R),r∈R,则ab+ba∈S(R),且rar*∈S(R).当然,如果*是一个恒等映射,那么R就成为一个交换环.本文涉及的扩*-亚序、*-亚序的定义和有关性质以及T-模、限制素*-理想、Jordan理想的定义均参见文献[3-7].
1 *-序的概念
定义1.1(参见文献[3]中定义1.2)设R是一个*-环,P是S(R)的一个子集,如果P满足如下条件:
(1)1∈P,-1∉P;
(2)P+P⊆P;
(3)r Pr*⊆P,∀r∈R;
(4)P⋃-P=S(R);
(5)∀a,b∈S(R),若aba∈P⋂-P,则a∈P⋂-P或b∈P⋂-P;
(6)若a,b∈P,则ab+ba∈P.
那么就称P是R的一个*-序.此时,集合P⋂-P称为*-序P的支集,并记为supp(P).如果P仅满足上述条件(1)-(5),那么称P为R的一个Baer-序.
定义1.2环R称为实*-环,如果R具有*-序.
注:本文中所述*-环R如不特别申明,则均指实*-环.由于R的特征为0,从而可认定Z⊂R,其中Z表示通常的整数环.此外,本文用N表示通常的自然数集.
定义1.3(参见文献[3]中定义1.2)设R是一个*-环,P是R的一个*-序,如果R的一个子集Q满足如下条件:
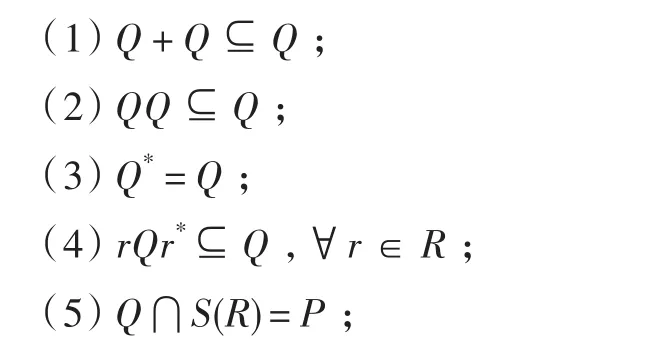
那么就称Q是P的一个扩*-序.
定义1.4环R中的一个理想I称为*-理想,如果I*=I.
定义1.5[7]环R的一个理想I(I≠R)称为素理想,如果a,b∈R且aRb⊆I可得a∈I或b∈I.
定义1.6I称为*-环R的素*-理想,如果I既是R的*-理想又是R的素理想;I称为*-环R的限制素*-理想,如果I是R的素*-理想与S(R)的交集.
定义1.7I称为*-环R的Jordan理想,如果I不仅是R的一个子加群且满足
若a∈I,b∈R,则ab+ba∈I.
2 扩*-亚序和T-模
首先叙述*-环R的扩*-亚序的定义[3].
定义2.1*-环R的元素r=rπ(1)…rπ(n)称为元素r1,…,rn的一个置换积,其中π是集合{1,…,n}的一个置换.
定义2.2*-环R的一个置换积称为关于元素r1,,…,rn,嵌套,如果这个置换积中的元素满足rj出现在元素ri,之间当且仅当元素出现在元素ri,之间.
定义2.3设R是一个*-环,且M⊆S(R).T是形如a1,…,al,b1,b1…,bm,bm,r1,,…,rn,,ai∈M,bj∈S(R),rk∈R,l,m,n>0的元素关于元素r1,,…,rn,嵌套的置换积的有限和生成的集合,则称T是*-环R的扩*-亚序.
注:*-环R的扩*-亚序T满足如下公理:(1)T+T⊆T;(2)TT⊆T;(3)rTr*⊆T,∀r∈R;(4)T=T*.用T0(R)表示R的由空集生成的扩*-亚序,则T0(R)是R的最小的扩*-亚序.
设a∈S(R),T是由S(R)的子集M生成的.则我们也能得到由M⋃{a}生成的扩*-亚序.这个扩*-亚序可以分解为T+T[a],其中T[a]表示为如下所有元素a,a1,…,al,b1,b1…,bm,bm,r1,,…,rn,,ai∈M,bj∈S(R),rk∈R,l,m,n>0,关于元素r1,…,rn,嵌套的置换积的有限和生成的集合.
定义2.4设T是*-环R的一个扩*-亚序,R的一个素*-理想p称为T-相容的,如果对于任意的s,t∈T⋂S(R),由s+t∈p都有s,t∈p.
命题2.5设T是*-环R的一个扩*-亚序,且p是R的一个T-相容的限制素*-理想,使得T⋂-T⋂S(R)=p.若T是R的满足上述条件的一个极大的扩*-亚序,则T⋂S(R)成为R的一个*-序.
证明显然,由文献[3]的注4.3知T[1]=T,从而1∈T⋂S(R).假如-1∈T.则1∈T⋂-T⋂S(R)=p.从文献[3]的定理4.7(1)知,存在*-环R的一个*-序P,使P⋂-P=p.从而1∈P⋂-P,即有-1∈P,矛盾于定义1.1(1),故-1∉T⋂S(R),T⋂S(R)+T⋂S(R)=(T+T)⋂S(R)⊆T⋂S(R).设a∈T⋂S(R),∀r∈R,则rar*∈T⋂S(R).这表明,r(T⋂S(R))r*⊆T⋂S(R).由于p是R的限制素*-理想,从而表明,对于任意的a,b∈S(R),aba∈(T⋂S(R))⋂-(T⋂S(R))=T⋂-T⋂S(R)=p,导致a∈p或b∈p.利用T是R的满足命题条件的一个极大的扩*-亚序,由文献[3]中的定理4.7的断言1和断言2知,S(R)⊆T⋃-T,即(T⋂S(R))⋃-(T⋂S(R))=S(R).最后,设a,b∈T⋂S(R),则ab+ba∈(TT+TT)⋂S(R)⊆(T+T)⋂S(R)⊆T⋂S(R).因此,T⋂S(R)成为*-环R的一个*-序.
命题2.6设T是*-环R的一个扩*-亚序,且p是R的一个限制素*-理想,则以下论断等价:
(1)存在一个扩*-亚序Q⊇T,使得Q⋂S(R)成为R的一个*-序,且supp(Q⋂S(R))=p;
(2)p是T-相容的.
证明(1)⇒(2):设R的一个扩*-亚序Q⊇T,使得Q⋂S(R)成为R的一个*-序,且supp(Q⋂S(R))=p.再设s+t∈p,其中s,t∈T⋂S(R),则s∈Q⋂S(R),且s∈-t+p⊆-Q⋂S(R).于是,s∈supp(Q⋂S(R))=p.同理可得,t∈p.这表明,p是T-相容的.
(2)⇒(1):设Q是由(T⋂S(R))⋃p生成的扩*-亚序.由文献[3]中命题4.6(2)知,Q⋂-Q⋂S(R)=p.再由文献[3]中命题4.6(1)知,Q⋂S(R)=T⋂S(R)+p.由于p是T-相容的,从而可知p是Q-相容的.由Zorn引理,可设Q为满足条件:Q⋂-Q⋂S(R)=p的一个极大的扩*-亚序.再由命题2.5知,Q正为(1)中所求.
推论2.7设p是*-环R的一个限制素*-理想,则以下论断等价:
(1)p是R的某个*-序的支集;
(2)p是T0(R)-相容的.
我们有如下T-模的定义[3].
定义2.8对于*-环R的一个扩*-亚序T,R的一个子集Q称为T-模,如果Q满足如下条件:

(4)对于任意的a∈Q⋂S(R),都有T[a]⊆Q.
以下设x∈S(R),用Z+表示Z中的非负元,且Z+[x2]表示如下集合:

显然,Z+[x2]⊂S(R),且对于*-环R的任意的扩*-亚序T都有,Z+[x2]⊆T.
命题2.9设T是*-环R的一个扩*-亚序,Q为R的一个T-模,使得T⊆Q,且-Z+[x2]⋂Q=ϕ.若Q是R的满足上述条件的一个极大的T-模,则有:
(1)p:=Q⋂-Q⋂S(R)成为S(R)的一个Jordan理想;
(2)S(R)⊆Q⋃-Q;
(3)Q⋂S(R)成为R的一个Baer-序.
证明(1)由于Q是R的一个T-模,从而p+p⊆p和-p=p显然成立.设Q′={b|b∈R,且2b∈Q},则Q⊆Q′.显然,Q′成为一个T-模.假若对于某个f(x2)∈Z+[x2],-f(x2)∈Q′,则-2f(x2)∈Q.从而-f(x2)=-2f(x2)+f(x2)∈Q,矛盾!因此,-Z+[x2]⋂Q′=ϕ.再由Q的极大性知,Q′=Q.
设r∈S(R),b∈p,则4rb=(r+1)2b+(r-1)2(-b)⊆T[b]+T[-b]⊆Q+Q⊆Q.再由Q′=Q知,rb∈Q.同理,-rb∈Q,即rb∈Q⋂-Q.类似地,br∈Q⋂-Q.从而,rb+br∈Q⋂-Q⋂S(R)=p.因此,p是S(R)的一个Jordan理想.
(2)设a∈S(R).假若a,-a∉Q,则Q+T[a]和Q+T[-a]都是T-模,且有T⊂Q+T[a]和T⊂Q+T[-a]成立.由Q的极大性知,存在f1(x2),f2(x2)∈Z+[x2],q1,q2∈Q,以及t1∈T[a],t2∈T[-a]使得

此时可设q1,q2,t1,t2∈S(R).因为,-f1(x2)-(f1(x2))*=q1+(q1)*+t1+(t1)*,其中-f1(x2)-(f1(x2))*∈-Z+[x2]⊆S(R),q1+(q1)*∈Q⋂S(R),t1+(t1)*∈T[a]⋂S(R).所以,在(2.1)中,不妨直接设q1,q2,t1,t2∈S(R).显然,(f1(x2))2f2(x2)∈Z+[x2].此时,
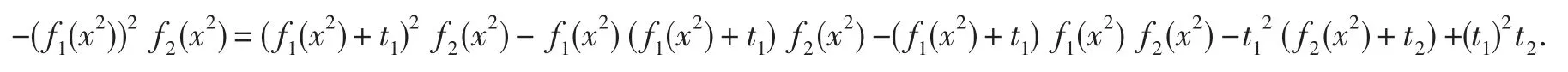
显然,(f1(x2)+t1)2f2(x2)∈T[f2(x2)]⊆Q.此外,由于f1(x2),f2(x2)∈Z+[x2]⊆T,-(f1(x2)+t1)=q1∈Q⋂S(R),且-(f2(x2)+t2)=q2∈Q⋂S(R).这表明,-f1(x2)(f1(x2)+t1)f2(x2),-(f1(x2)+t1)f1(x2)f2(x2),-t12(f2(x2)+t2)∈Q.最后,由于-t1=q1+f1(x2)∈Q⋂S(R),且t1t2∈T[a]T[-a]⊆-T[a]T[a]⊆-T.于是,(t1)2t2.=(-t1)(-t1t2)∈Q.这表明,-Z+[x2]⋂Q≠ϕ,矛盾!从而a∈Q或-a∈Q.由a在S(R)中的任意性即知,S(R)⊆Q⋃-Q.
(3)证明类似于文献[3]中的定理5.2.
推论2.10设T是*-环R的一个扩*-亚序,使得-Z+[x2]⋂T=ϕ.若T是R的满足上述条件的一个极大的扩*-亚序,则T⋂S(R)成为R的一个*-序.
证明由所设可知,R有一个T-模Q,使得Q⊇T且-Z+[x2]⋂Q=ϕ,比如取Q=T.由Zorn引理,可进一步设这个Q是极大的.假若Q⋂S(R)≠T⋂S(R),则存在a∈Q⋂S(R)T⋂S(R)使得T+T[a]是R的一个扩*-亚序,且T⊂T+T[a].由于T+T[a]⊆Q,从而-Z+[x2]⋂(T+T[a])=ϕ.这与题设矛盾!因此,Q⋂S(R) =T⋂S(R).再由命题2.9知,T⋂S(R)是R的一个Baer-序.此外,由于T对于乘法是封闭的,从而知T⋂S(R)还满足定义1.1的条件(6),即:若a,b∈T⋂S(R),则ab+ba∈T⋂S(R).于是,T⋂S(R)成为*-环R的一个*-序.
[1]Holland S S.*-Valuations and Ordered*-Field[J].Trans Amer Math Soc,1980,262(1):219-243.
[2]Prestel A.Lectures on Formally Real Fields[M].New York:Springer-Verlag,1984:1-14.
[3]Marshall M.*-Ordering on a Ring with Involution[J].Comm Algebra,2000,28(3):1157-1173.
[4]Craven T,Smith T.Ordered*-Rings[J].J Algebra,2001,238:314-327.
[5]Molina M S.Orders in Rings with Involution[J].Comm Algebra,2001,29(1):1-10.
[6]Dai Zhizhong.Real Places and Real Valuations on a Commutative Ring[J].Acta Math Sinica,New Series,1994(10),Special Issue (Jan):24-29.
[7]Lam T Y.A First Course in Noncommutative Rings[M].New York:Springer-Verlag,1991:275-292.
Extended*-preorderings and Real*-ring
JIANG Wei1,HUANG Dong-ming2
(1.School of Mathematics and Statistics,Changshu Institute of Technology,Changshu 215500,China; 2.College of Information Science and Technology,Hainan University,Haikou 570228,China)
In order to describe the reality of a*-ring,the authors of this paper investigate some interplays be⁃tween the extended*-preorderings(or T-modules)and*-orderings on a*-ring.
*-ring;*-ordering;extended*-preorderings;real algebra
O153.5
A
1008-2794(2013)04-0001-04
2013-03-15
江苏省2010年度高校“青蓝工程”优秀青年骨干教师项目(苏教师〔2010〕27号)
姜伟,副教授,博士,研究方向:代数学,E-mail:jiangwei@cslg.cn.
*-环的概念是由*-域[1]的概念推广出来的.所谓*-域,是指带有一个对合映射*的斜域.有序的*-域有许多类似于实域的结果[2].近来,M.Marshall[3-4]已经把*-域的*-序概念推广到了*-环上,发展了*-环的*-序的有关理论.为了进一步研究*-环的实性,本文探讨了*-环的扩*-亚序、*-亚序和*-序的一些联系.在取定一个扩*-亚序T的基础上,进一步探讨了由M.Marshall在文献[3]中引进的T-模和*-序的一些联系.

