一类非线性系统的有限时间输出反馈镇定问题

谢晶，陈宝凤

（安阳工学院数理学院，河南安阳 455000）

一类非线性系统的有限时间输出反馈镇定问题

谢晶，陈宝凤

（安阳工学院数理学院，河南安阳 455000）

研究了一类连续非线性系统的有限时间镇定问题.基于有限时间稳定的Lyapunov理论和“加幂积分器”的方法给出了一个动态输出反馈控制器的设计步骤，解决了这类非线性系统的有限时间镇定问题.

非线性系统；有限时间镇定；加幂积分器

自Peter Dorato于1961年提出了短时间稳定性（Short Time Stability）[1]（即有限时间稳定性）的概念以来，有限时间稳定与镇定问题受到了较大的关注，得到了广泛的研究[2-10]，形成了有限时间稳定的Lyapunov理论和各种设计有限时间稳定控制器的方法.有限时间镇定是指在有限时间内将系统控制到平衡点.研究表明，有限时间收敛的系统具有更好的鲁棒性能和抗干扰性能.

文献[2]确立了有限时间稳定的基础理论，给出了一个连续自治系统的有限时间稳定性判定定理.文献[3-4]基于齐次性理论，给出了双重积分器系统的状态反馈和动态输出反馈的有限时间镇定设计方法.文献[5-10]利用构造性控制设计方法解决了几类非线性系统的全局有限时间镇定问题.本文将文献[5]的成果拓展到更一般的高阶非线性系统，利用有限时间稳定的Lyapunov理论和“加幂积分器”的方法构造出了一个输出反馈控制律，使得这类系统在有限时间内达到全局稳定.

1 问题的提出及预备知识

在本文中，考虑一类具有如下形式的非线性系统的有限时间输出反馈镇定问题：

下面关于系统（1）做如下假设：

（2）取r如假设（1）所示，系统（1）满足下式

我们的研究目标是设计一个动态输出反馈控制器

使得系统（1）-（2）是全局有限时间稳定的.

下面给出一些重要引理[11]：

引理1对于∀xi∈R，y∈R，i=1,…,n，0＜b≤1，下列不等式成立：

引理2令c,d为正实数，γ(x,y)＞0是一个实值函数，那么

2 控制器设计

这部分我们利用“加幂积分器”的方法[6]设计一个状态反馈控制器.

由引理1和引理2得：

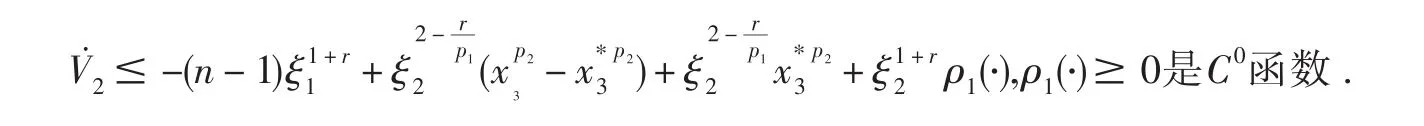
步骤3（归纳假设）：

假设在第k-1步，存在一个C1正定的，适定的Lyapunov函数Vk-1(x1,…,xk-1)，满足

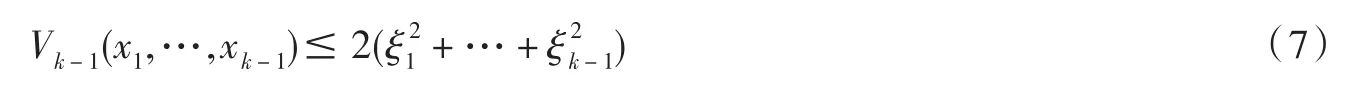
定义虚拟控制如下：

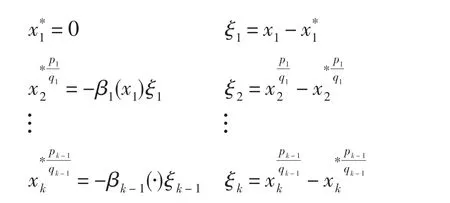
其中，β1(⋅)＞0,…,βk-1(⋅)＞0是C1函数，使得

下证在第k步中，不等式（7）和（8）也成立.

估计上式右端各项.首先，由引理1和引理2得：

为了控制器的建立给出下面两个命题[5]：

命题1对于k=1,…,n，存在C0函数(x1,…,xk)≥0，使得

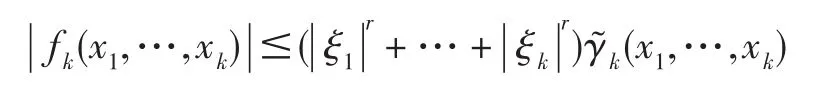
命题2对于l=1,…,k-1，存在C1函数Ck,l(x1,…,xk)≥0，使得

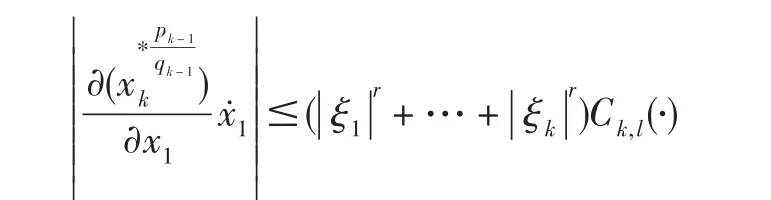
利用命题1和引理2得

估计（9）式的最后一项，由命题2得：

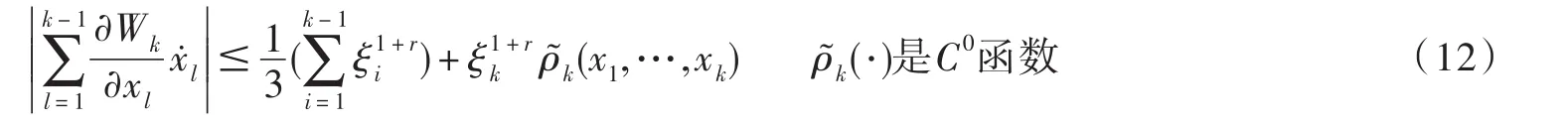
将（10）-（12）式代入（9）式，得：

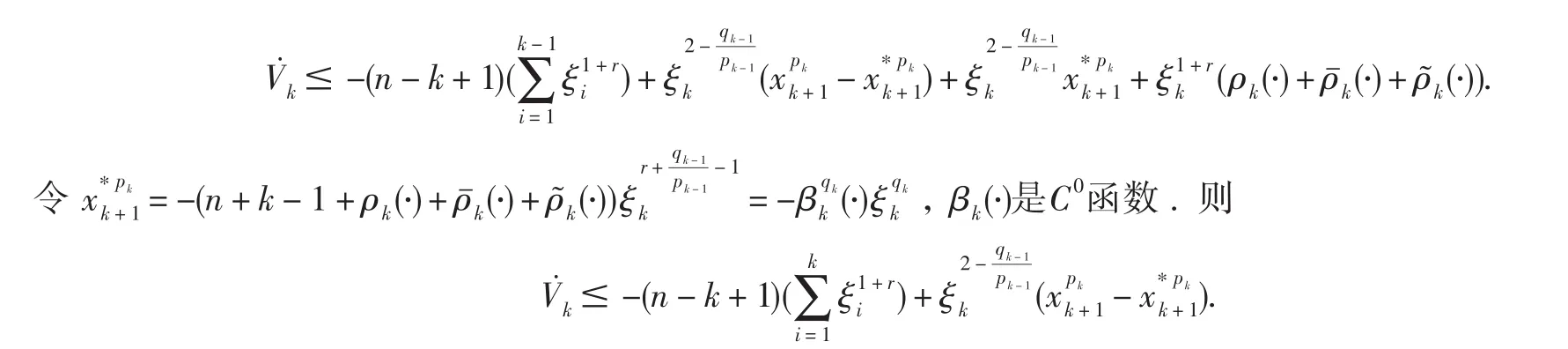
下面设计一个n-1维观测器：

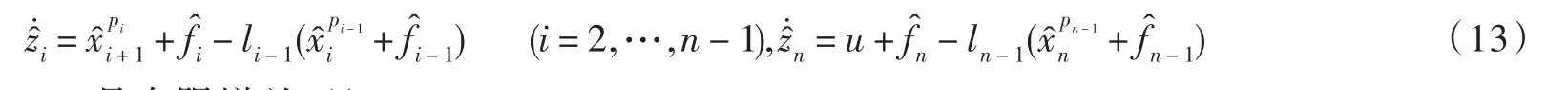
在这儿，li＞1(i=1,…,n-1)是有限增益，且

则存在一个常数k＞0，使得下式成立：

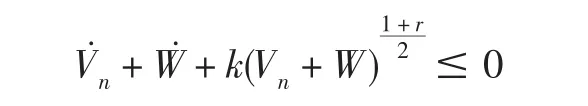
由Lyapunov稳定判定定理得闭环系统（1）-（13）-（14）是全局有限时间稳定的.

[1]Dorato P.Short time stability in linear time-varying systems[C].New York:In Proceedings of the IRE International Convention Record Part 4,1961:83-87.

[2]Bhat S P,Bernstein D S.Finite-time stability of continuous autonomous systems[J].SIAM Journal on Control and Optimization, 2000,38(3):751-766.

[3]Bhat S P,Bernstein D S.Continuous finite-time stabilization of the translation and rotational double integrators[J].IEEE Transaction on Automatic Control,1998,43(5):678-682.

[4]Hong Y,Wang J,Xu Y.On an output feedback finite-time stabilization problem[J].IEEE Transaction on Automatic Control,2001, 46(2):305-309.

[5]Qian C,Lin W.A continuous feedback approach to global strong stabilization of nonlinear systems[J].IEEE Transaction on Automatic Control,2001,46(7):1061-1079.

[6]Haimo V T.Finite-time controllers[J].SIAM Journal on Control and Optimization,1986,24(4):760-770.

[7]Hong Y.Finite-time stabilization and stabilizability of a class of controllable systems[J].Systems and Control Letters,2002,46(4): 231-236.

[8]Hong Y,Jiang Z.Robust finite time control of nonlinear systems with dynamic uncertainty[R].Minneapolis:Proceedings of the 2006 American Control Conference,June 14-26,2006:4303-4307.

[9]Jiang Z,Praly L.Design of robust adaptive controllers for nonlinear systems with dynamic uncertainties[J].Automatica,1998,34(7): 835-840.

[10]Jiang Z,Mareels I.Robust nonlinear integral control[J].IEEE Transaction on Automatic Control,2001,46(8):1336-1342.

[11]Beckenbach E,Bellman R.Inequalities[M].Berlin:Springer-Verlag,1971.

Output Feedback Finite Time Stabilization of a Class of Nonlinear Systems

XIE Jing,CHEN Bao-feng
（School of Mathematics and Physics，Anyang Institute of Technology，Anyang 455000,China）

The finite time stabilization is investigated for a class of nonlinear systems.An output feedback con⁃troller is designed by using the Lyapunov theory of finite time stability and adding a power integrator technique to solve the finite time stabilization problem of the nonlinear systems.

nonlinear systems；finite time stabilization；adding a power integrator

TP273

A

1008-2794（2013）04-0009-04

2013-03-29

谢晶，讲师，硕士，研究方向：非线性系统，E-mail：xiejingay@126.com.