电磁隐身斗篷奇异性问题的处理与分析

庞旭东 朱守正

（华东师范大学信息科学与技术学院，上海200241）

引 言

近年来，电磁隐身斗篷/隐身罩（cloak）的研究成为新型隐身技术的研究前沿.电磁隐身斗篷是基于变换电磁学［1］和电磁超材料这两方面的研究理论新兴发展形成的一种新颖隐身设计策略.其基本思路是基于Maxwell方程组在不同坐标空间下的形式不变性，将原始空间中的一个实心区域压缩变换到变换空间中的一个空心区域，该空心区域具有特定的各向异性非均匀介电常数和磁导率张量，这就是所要设计的隐身斗篷［2］.在变换过程中斗篷外边界以外区域的材料参数保持不变，而变换空间中斗篷内边界以内区域则成为隐身区.经典圆柱型隐身斗篷［1-2］是最早被提出的一类斗篷模型，整个变换过程可以看作是将原始空间的中心点通过坐标变换的方法扩展映射为变换空间的内边界圆，这种直接的扩展式映射方法带来一个基本难题：在原始空间，入射波通过中心点的时间是零，但是在变换空间，这个中心点被扩展为一个二维圆孔，由此推理，在变换空间中，入射波在隐身斗篷内边界圆上的传播速度需达到无穷大，才能使其通过这段半圆路程的时间也是零.这样，上述扩展映射式隐身斗篷在理论上碰到一个奇异性问题，导致其计算所得材料的参数将非常极端，可能会趋于零值或无穷大值.这也使得在实际实现中，此类变换电磁学器件只能局限于微波频段或窄带应用［2］.

针对电磁隐身斗篷在上述坐标变换过程中产生的奇异性问题，本文讨论了三类不同的处理方法.第一类“参数简化法”的研究比较成熟［3-5］，本文通过表格对常见的圆柱型线性变换斗篷的材料参数公式做了简要的对比与总结，阐述了其中的变换规律与实质意义.第三类“非欧空间变换法”，是较新提出的变换理念，本文结合引用文献做了简要说明.重点讨论了第二类“渐变维度扩展法”，这方面的研究较少，虽有相似文献［6-8］给出空间变换的部分公式与仿真结果，但是其一，从数学拓扑学角度对这类空间变换本质的讨论还比较欠缺，其二，对这类空间变换材料参数的具体数值及其分布范围的变化情况的研究也非常缺乏.本文利用有限元分析软件Comsol Multiphysics对渐变维度扩展法中两种不同的方案进行了仿真计算，给出了材料参数各分量的分布图、具体数据曲线以及归一化参数分布范围的变化规律，从空间拓扑学角度给予了解释，完善了对隐身斗篷空间变换过程的研究.

1 隐身斗篷奇异性问题的处理方法

对于一个二维隐身斗篷，由于局部各向异性以及空间上的不均匀性，在内边界材料参数通常会出现极值情况（∞/0），这个奇异性问题严重限制了器件的实际可实现性.目前研究中，涉及此问题的方法较多.从数学表述和物理涵义角度，可以概括为以下三种方法：1）参数简化法；2）渐变维度扩展法；3）非欧空间变换法.第一类方法的研究已经比较成熟［3-5］，但缺少统一性；第二类处理方法研究较少，部分相似工作已有研究［6-8］；第三类处理方法也称广义隐身斗篷［9］，是新提出的一种理论解决方案.

1.1 参数简化法

隐身斗篷的研究始于J B Pendry，D Shurig等在2006年发表的论文［1-2］，文中涉及到材料参数极值问题以及在实验中的近似处理方法.在此基础上经过研究改进，逐渐发展成为参数简化法.其中，文献［3］采用等效色散关系条件来调整材料的参数值，文献［4］提出一种将本身不包含奇异性的三维斗篷投影到其横截面上的镜像映射法来处理奇异性问题，文献［5］就线性/非线性映射扩展方式的参数简化过程做了详细介绍.上述文献得到了类似的简化参数表达式［5］.以二维圆柱型斗篷为例，采用简单的线性变换方式，表1列出了理想模型、简化模型1、简化模型2的材料参数表达式［5］.

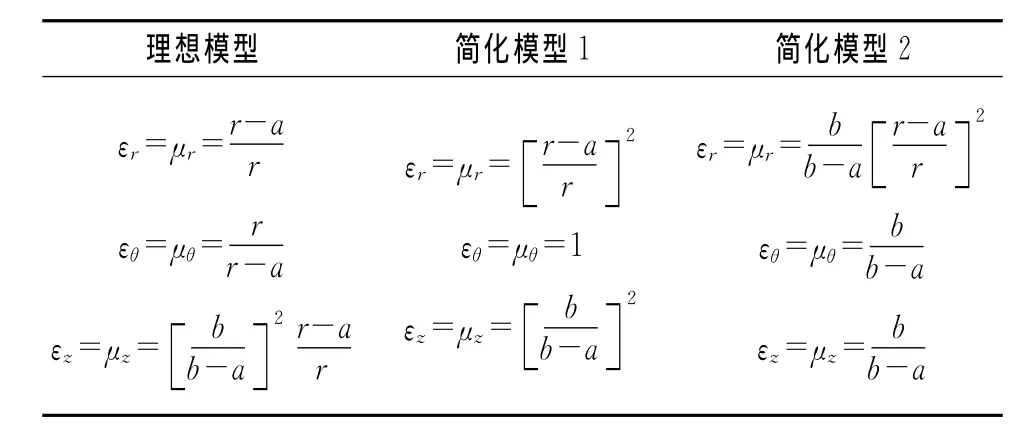
表1 圆柱型线性变换斗篷的材料参数

表1中，a为变换空间中内圆半径，b为外圆半径。令τ＝（r-a）/r（a≤r≤b），可以发现：理想模型三个方向参数表达式中都含有τ因子，当r＝a时，τ＝0，r与z方向的参数值都将等于零，同时θ方向的参数值变为∞，即理想模型三个方向的参数值都存在极值.处理方法：保持μθεz和μrεz的值不变，将表达式中的τ因子同时抵消掉，从而将三个方向上的奇异性集中到径向r方向上以方便处理，最终得到简化模型的参数表达式.

结论：参数简化法的实质是将三个不同维度方向上的奇异性通过抵消因子归集到其中某一个方向上，比如r方向，而其他方向（θ，z）的材料参数值保持常量，这样就明显降低了实际制备的难度.虽然简化参数后的斗篷隐身性能有所下降，但仍然具备一定的隐蔽效果，简化模型除了在r方向上的参数值会要求零值以外，其他参数都达到可实现的条件，相比于理想模型，对材料参数的要求显著改善.

1.2 渐变维度扩展法

在数学拓扑学概念中，维度又称维数，是数学中独立参数的数目.点、线、面、体的维度分别是零维、一维、二维和三维.二维经典隐身斗篷中的方法是将原始空间中心点扩展映射为一个空心圆（内边界圆），是零维到二维的拓扑学变换，这个过程中有了维度上的跃变，入射波经过一个零维点的时间为零，当路程变为二维半圆πa时，必然会出现奇异性问题.针对以上路程差的矛盾，以下面两种维度渐变式处理方案来详细说明.

1.2.1 方案一：同维度变换法

同维度变换法在空间变换过程中不发生维度变化，内边界圆从r＝s的小圆开始变换为r＝a的圆，仅是二维图形之间的变换.对于这种空间变换，采用扩展式坐标变换法，材料参数的极值问题可以得到明显改善.来描述，对二维模型就是散射宽度.由于用有限元法的计算结果是近场数据，需要运用Huygens原理将其转化为远场数据再进行计算.计算散射宽度的公式为

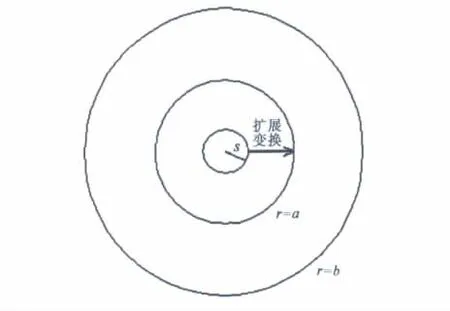
图1 圆柱型同维变换斗篷空间变换示意图

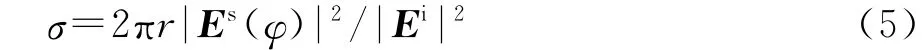
利用上述方法分别对图2（a）、（b）中两种情形的散射宽度值进行了计算，结果如图2（c）、（d）所示.可以发现：图2（c）、（d）的散射宽度值基本一致，并且符合图2（a）、（b）的仿真结果.这种情况下隐身斗篷的材料参数分布如图3所示.

图1为这种方案的示意图，将斗篷原先的内边界r＝s扩展延伸到新的内边界r＝a上.从整体空间上可以看作是将圆环s≤r≤b区域压缩为圆环a≤r≤b，其中环形区域s≤r≤a为隐身区.采用线性变换，坐标变换表达式如下［6］：

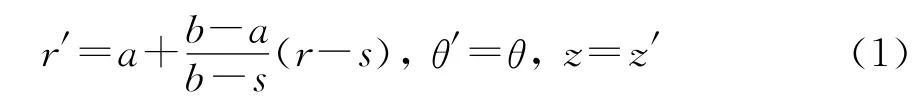
在柱坐标系中，变换后的材料参数表达式如下［7］：

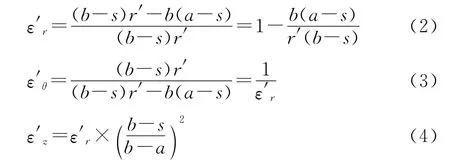
从文献［6-8］中的理论可以知道：依照上述同维度空间变换设计的圆柱型斗篷的散射模式等效于半径为s的理想导电体（PEC）小圆环.以下用有限元分析软件Comsol Multiphysics进行了严格的仿真验证，所选斗篷内外半径分别为a＝0.25m，b＝0.5 m.仿真计算采用柱面波照射，在波源距离相当远时柱面波可以近似为平面波［10］.首先取s＝0.10m上述斗篷在f＝2GHz柱面波的照射下产生的散射模式，如图2（a）、（b）所示，波源距中心的距离d＝1.442m.从中可以发现，所设计斗篷的散射效果基本等效于半径0.10m的PEC小圆环的散射效果.为了给出更加定量化的指标，这里使用散射截面［12］

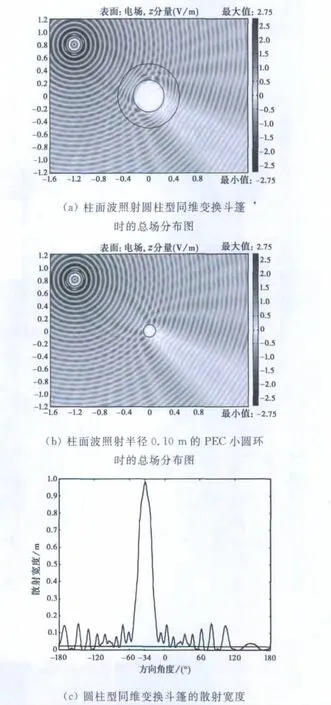
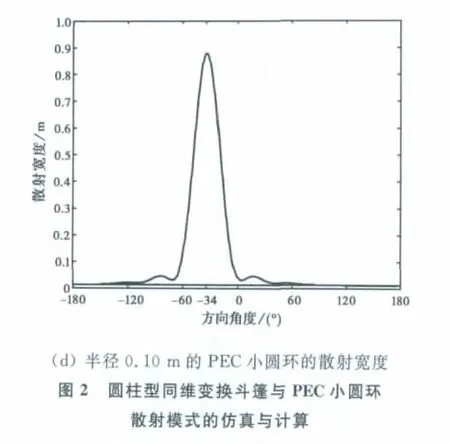
图3是s＝0.10m时的ε各分量参数的具体分布情况，灰度由深到浅对应数值由低到高.从图中可以发现εxx与εyy的变化范围相同；εxy包含正负数值，绝对值相等，因此记作｜±εxy｜；εzz沿径向r逐渐增大.

减小s的大小至0.05m，与图2中的仿真结果类似，这时同维变换斗篷在柱面波的照射下产生的散射模式等效于半径0.05m的PEC小圆环的散射模式，其材料参数的具体值可查看图4（a）、（b）.

参数分析：随着s的减小，隐身斗篷材料参数的分布范围在增大，实际制备难度也逐渐增加［11］.为了充分展示各方向材料参数ε的极值随不同s值变化的详细信息，图4列出了各方向ε极值随s的变化曲线，图4（a）是｜±εxy｜max和εxx｜max＝εyy｜max＝εθ｜min随不同s值的变化曲线，这四组数据纵轴分布范围较大，所以共同放在图4（a）中表示.图4（b）中从上往下曲线（1），（2），（3），（4）分别表示的是εzz｜max＝εθ｜min，εzz｜min，εr｜max，εxx｜min＝εyy｜min＝εθ｜min随不同s值的变化曲线，由于这七组数据纵轴变化范围较小，所以共同放在图4（b）中以方便对比.图中所有曲线都用不同的标记加以区别，坐标横轴s的单位是厘米，0≤s≤a.

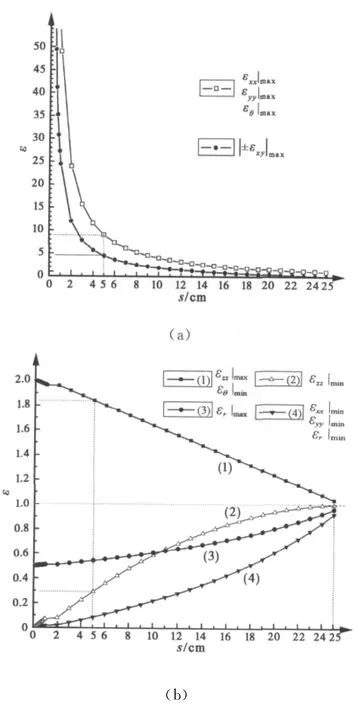
图4 各方向ε极值随s的变化曲线

s值越小，这种空间变换对原始空间的挤压率越高，设计斗篷所需的材料参数也越苛刻.若s＝0，公式（2）～（4）将化简为表1中理想模型的参数表达式，材料参数也将全部出现极值.为了形象表示空间挤压率和材料参数变化范围之间的具体关系，在图4的基础上进一步整理出图5—各方向材料参数的归一化分布范围η随s的变化曲线，其中η＝（εmaxεmin）/εmax×100%，具体某个方向的极值可以由图4中的数值代入.坐标横轴s值越小表示空间挤压度越高，当s→0时，η→100%，表示此时材料参数的分布范围极大，实际情况中将无法实现.而当s→a时，η→0% ，表示此时的材料参数分布均匀.这里的η也可以表示斗篷材料参数的实际制备难度.在图5中，曲线（a）表示r，θ，z方向的η值曲线，呈线性变化；曲线（b）表示xx和yy方向的η值曲线，呈圆弧曲线变化.s＝0.10m 时ηr，θ，z＝60%，具有很强的实际可实现性.

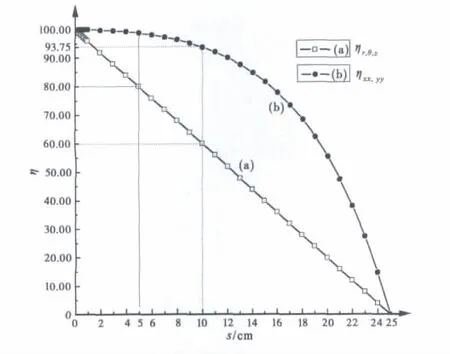
图5 各方向材料参数归一化分布范围η随s的变化曲线

结论：利用同维度空间扩展法，虽然不能达到完美隐身，但是在有限范围的材料参数下，所构建的隐身器件的确能达到一定的隐蔽效果.整个隐身器件的散射模式仅等效于一个PEC小环的场分布（图2），成功地将一个分米级物体的散射截面减小到厘米级，既让待隐身物体具备了较强的隐蔽性能，同时又避免了参数的极值问题.

1.2.2 方案二：线变换式扩展法

线变换式扩展法：内边界图形以一条经过坐标中心的短线段开始，变换为一个两维环状斗篷，这种从一维过渡到二维的维度连续阶变过程，没有维度上的跃变，也能减缓奇异性.以下是以二维椭圆型斗篷为例进行的仿真验证.

如图6所示，经过坐标中心的短线段L的长度为l，内、外椭圆的短半轴长度分别为a、b，椭圆的轴比都是2.如图6所示，斗篷内边界从线段L开始扩展到内椭圆x2/（2a）2＋y2/a2＝1处，这样除了线段L以外的内椭圆区成为隐身区域.具体的坐标变换及参数表达式可以参考文献［6-7］.

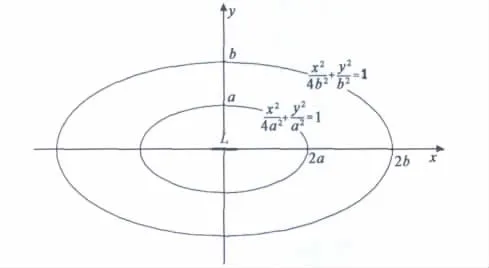
图6 线变换式椭圆斗篷空间扩展示意图

仍采用有限元分析软件Comsol Multiphysics进行仿真验证：a＝0.1m，b＝0.2m，线段L的长度l＝0.02m，此次采用f＝4GHz的柱面波进行照射，波源距中心的距离d＝0.721m.采用0.02m的PEC短截线来进行散射效果的对比参照，PEC短截线如线段L一样横向放置.仿真结果如图7所示.

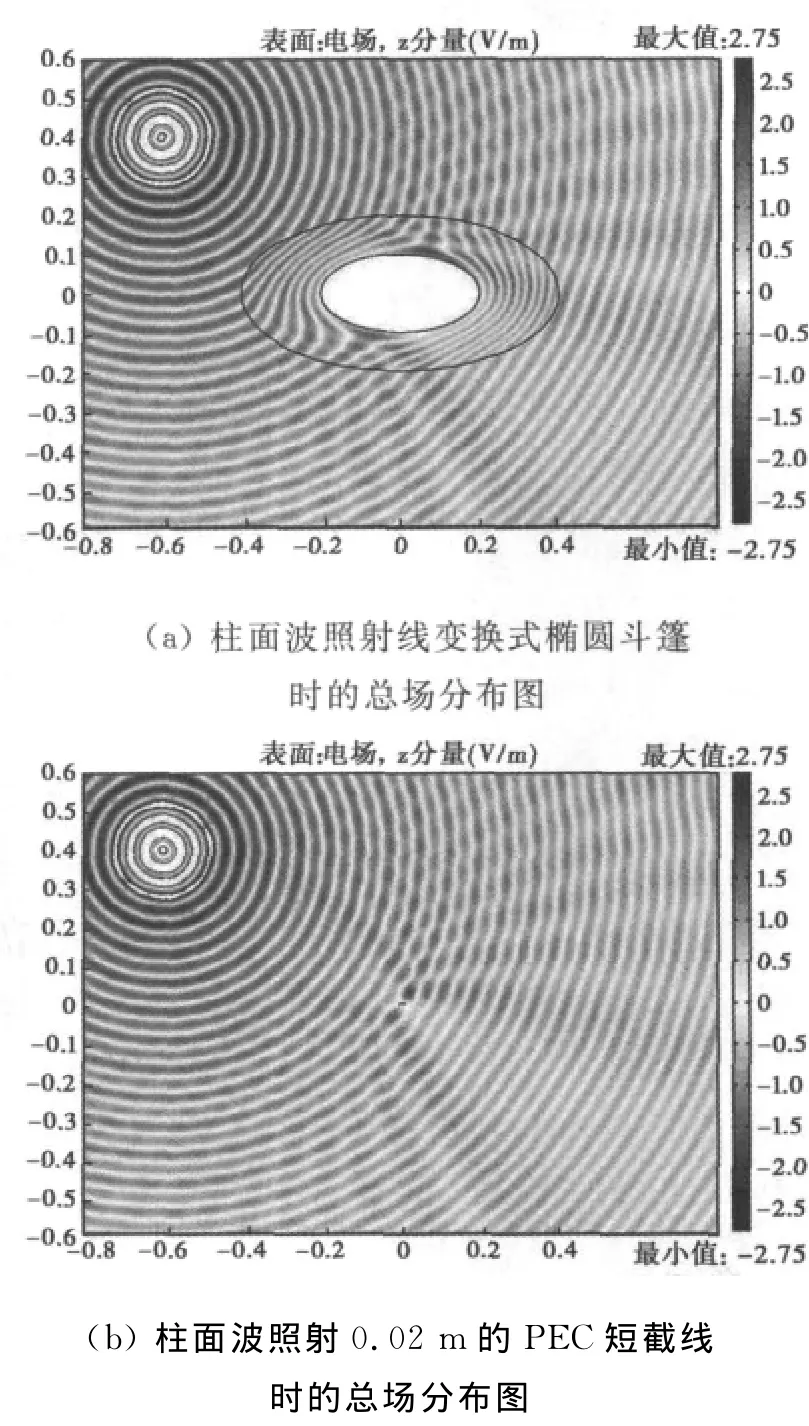
图7 线变换式椭圆斗篷与PEC短截线的仿真验证

从图7可以看出这种线变换式椭圆斗篷的方案是可行的，其散射情况基本上等效为PEC短截线的散射模式.对图7（a）、（b）两种情况的散射宽度值也进行了计算，两者分布情形相似，其散射宽度的峰值均接近5cm.上述斗篷材料参数仍然存在较大极值，但这些极值只集中在椭圆内外边界很小一部分区域，忽略后简化的椭圆斗篷参数分布情况见图8所示.

从拓扑学可以知道这种维度阶变的斗篷只能减缓奇异性问题，不能完全消除，数值仿真结果也给出了验证.原因是：就x、y坐标分向量而言，图形x分量的变化中维度没有变化，只是1维线段长度的拓宽；但y分量变化时则出现了点到线的变化（0维扩展到1维），有了维度阶变所以会产生一定的奇异性，影响散射效果.

结论：理想模型中0维到2维的维度跃变实质上是x、y两个分量方向中0维到1维维度阶变的叠加.方案二线变换式扩展法只消除了其中一个方向（x方向）的维度阶变，仍然存在一定的奇异性，但其隐身效果比较明显，器件的散射截面［12］显著减小，在雷达隐身等领域有着广泛应用.

1.3 非欧空间变换法

上述两种方案都是基于扩展式映射理论，对于奇异性问题做出了一定的改善。另一种补救的方法是采用保角映射方法使得波束绕行过某个区域.扩展式映射与保角映射都是尝试控制波束绕行过某个区域，然而扩展式映射只能工作于很窄的带宽，而保角映射理论却可以在坐标变换过程中采用非欧几里德形状的空间作为变换起点，进而可以消除材料参数的极值现象，故后者存在宽带实现的可能［9］.

图9中原始空间是由一个平面和球表面组成，两者接触于一条连接线上，而图9（1）是这个非欧空间在二维平面上的投影，其附带的坐标格也被映射到二维平面上.入射波由平面进入球面行进一周后沿原方向传播出去，图中外部圆圈规定了该装置的外边界，平面与球面接触的曲线投影在图中呈现出眼睛状图形，有关本图的详细解释可以参考文献［9］.文献中只是提出任何入射波在平面上的投影轨迹都不会经过图9（1）中的线段s，但没有给出更详细的图例解释，这里给出了入射波两种极端情况下的轨迹路径示意图，可以更清楚地解释这类非欧空间变换方法.

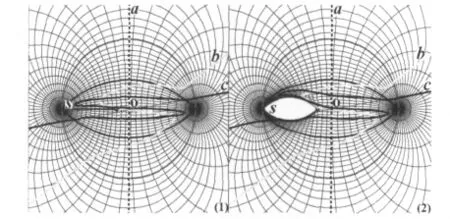
图9 二维非欧隐身装置图解［9］

如图9（1）中所示，虚线a表示波束垂直入射的情况，同时虚线a也是整个投影平面中坐标格最平坦处，所以其投影轨迹呈现为一条直线；黑色曲线c几乎是水平入射非欧隐身装置的，这种情况下，坐标格越密集的区域入射波的投影轨迹也弯曲得越明显.曲线b是介于这两种极端情况下的一般入射波轨迹投影.最终入射波都会保持原有方向继续传播，从而器件具备了潜在的隐身功能.图9（2）是在图9（1）的基础上将投影线段s扩展为一个二维的隐身区域，s周围的坐标格将被进一步挤压，曲线b和c也将受到一定的扭曲.文献［9］的研究显示，此类非欧隐身装置的材料参数分布范围较小，基本消除了参数极值问题.

2 结 论

本文针对扩展映射式隐身斗篷的奇异性问题，归纳分析了三类不同的处理方法，重点讨论了第二类维度渐变扩展法.

参数简化法，将材料参数的极值归集到其中一个方向上，降低了实际制备的难度，同时仍然具备一定的隐蔽效果.

渐变维度扩展法，方案二消除了变换空间中一个方向的维度阶变，从拓扑学角度来看是一种折中处理方法；方案一彻底消除了维度上的阶变，使得材料参数基本不会出现极值.这两种方案虽然都无法达到完美隐身，但是待隐蔽物体的散射截面明显降低，同时又基本避免了参数极值问题，在实际中有着更广的应用.

非欧空间变换法，理论上不同于前两者，涉及到广义相对论在现代电磁领域中的应用［13］，本文未对其作详细介绍，但这种方法有可能根本性解决奇异性问题.

［1］PENDRY J B，SCHURIG D，SMITH D R.Controlling electromagnetic fields［J］.Science，2006，312（5781）：1780-1782.

［2］SCHURIG D，MOCK J J，JUSTICE B J，et al.Metamaterial electromagnetic cloak at microwave frequencies［J］.Science，2006，314（5801）：977-980.

［3］HU Jin，ZHOU Xiaoming，HU Gengkai.Nonsingular two dimensional cloak of arbitrary shape［J］.Appl Phys Lett，2009，95（1）：011107.

［4］ZHANG Pu，JIN Yi，HE Sailing.Obtaining a nonsingular two-dimensional cloak of complex shape from a perfect three-dimensional cloak［J］.Appl Phys Lett，2008，93（24）：243502.

［5］YAN Min，RUAN Zhichao，QIU Min.Scattering characteristics of simplified cylindrical invisibility cloaks［J］.Opt Express，2007，15（26）：17772-17782.

［6］CHEN Huanyang.Transformation optics in orthogonal coordinates［J］.J Opt A：Pure Appl Opt，2009，11（7）：075102.

［7］LUO Yang，ZHU Shouzheng.Design of electromagnetic cloaks with the same scattering patterns of a reduced perfect electric conducting line or ring［J］.Phys Rev E，2010，82（3）：036606.

［8］JIANG W X，CUI T J，YANG X M，et al.Invisibility cloak without singularity［J］.Appl Phys Lett，2008，93（19）：194102.

［9］LEONHARDT U，TYC T.Broadband invisibility by non-Euclidean cloaking ［J］.Science，2009，323（5910）：110-112.

［10］杨晶晶，黄 铭，吴中元，等.TE波辐射下超材料正方形电磁斗篷特性分析［J］.电波科学学报，2009，24（1）：148-151.YANG Jingjing，HUANG Ming，WU Zhongyuan，et al.Study of metamaterial electromagnetic cloak with square volume under TE wave irradiation［J］.Chinese Journal of Radio Science，2009，24（1）：148-151.（in Chinese）

［11］林 振，梁昌洪.不同负相对折射率材料的FDTD分析［J］.电波科学学报，2007，22（1）：79-82.LIN Zhen，LIANG Changhong.Analysis of different negative refractive index materials by FDTD method［J］.Chinese Journal of Radio Science，2007，22（1）：79-82.（in Chinese）

［12］杨小鹏，赵维江，黄立伟.目标RCS的计算和对消效果的统计分析［J］.电波科学学报，2002，17（1）：88-92.YANG Xiaopeng，ZHAO Weijiang，HUANG Liwei.Calculation of RCS of targets and statistical analysis of cancellation effect［J］.Chinese Journal of Radio Science，2002，17（1）：88-92.（in Chinese）

［13］LEONHARDT U，PHILBIN T G.General relativity in electrical engineering［J］.New J Phys，2006，8：247.