分布式多入多出正交频分复用快衰落感知估计
周小平 李 莉 汪 敏 方 勇 张 静
(1.上海师范大学信息与机电工程学院,上海200234;2.上海大学通信与信息工程学院 特种光纤与光接入网重点实验室,上海200072)
引 言
正交频分复用(OFDM)技术在无线环境中具有多径衰落和窄带干扰的特性,而分布式多输入多输出(Distributed MIMO)技术具备对抗大尺度衰落的优点和良好的覆盖范围,将两者相结合组成分布式MIMO-OFDM系统[1-2]可以发挥各自的优势,提供更大的自由度,极大地提升了的系统能力,拓展了应用领域.同时,由于具有更加复杂的天线构型、处理算法,分布式MIMO-OFDM在系统优化、波形设计、系统同步、信号处理等方面存在很多新的问题和挑战[3-4].特别,在快衰落环境下,由于分布式 MIMO天线分布于小区中不同地理位置,与传统MIMO-OFDM系统相比,不但存在天线间干扰,而且还受到更强的快衰落信道干扰的影响.
为了提高高速移动分布式MIMO-OFDM系统的容量,各天线均需要信道状态信息对信道进行均衡和数据检测,信道状态信息的准确与否,将直接影响系统的整体性能.因此,需要对信道状态信息及时进行估计.但在快衰落环境中,对分布式 MIMOOFDM信道进行估计存在很大困难.传统导频辅助的信道估计方法[5-7],每根发送天线的导频插入比例需要满足奈奎斯特采样频率条件,即受信道衰落程度的影响.然而该条件是建立在无线信道传播于丰富散射环境的基础上,并没有考虑快衰落分布式MIMO-OFDM信道具有可稀疏性.而采用压缩感知理论(CS)[8-9]对快衰落信道进行估计时,将不再受到奈奎斯特采样定理的限制,只要信道在某个变换域,具有可稀疏性,各天线测量导频数可大为减少.对于单输入单输出(SISO)系统,文献[10-11]提出了基于压缩感知OFDM信道估计方法.而对于传统MIMO-OFDM系统,文献[12-13]提出了基于压缩感知的时频双选择性衰落信道估计方法.与传统MIMO-OFDM系统相比,分布式MIMO-OFDM系统由于天线分布于小区中不同理位置,位于不同站点的天线经历不同的相对路径损耗、阴影衰落,存在更强的天线间干扰.同时,由于接收端高速移动,分布于不同地理位置的发送天线经过各自多径时延到达各接收天线时,各信道间快衰落频度、衰落宽度、衰落深度和衰落余量等差别很大.在高速移动情况下,为了便于分析,采用传统信道估计方法用于分布式MIMO-OFDM系统时,通常假设分布于不同位置的发送天线到达移动端接收天线的信道之间阴影衰落相互独立,导致接收端难以获得准确的信道状态信息.实际测量表明:当移动终端在高速移动情况下,由于各发送天线和各接收天线之间无法达到足够远,各信道之间阴影衰落存在互相关性和干扰性,其与收发天线之间的距离、周围的环境和接收信号的到达角度都有关.
针对分布式 MIMO-OFDM系统,该文将充分利用分布式MIMO-OFDM系统快衰落信道间的感知数据在空间、时延和多普勒频移上具有的互相关性和干扰性,求取信道的联合稀疏模型.推导预相关随机导频测量矩阵,结合分布式压缩感知算法,以能量有效的方式对快衰落信道间稀疏冲激响应系数进行联合压缩测量和重构,得到各分布式MIMO接收端任意的稀疏信道系数.该方法可以明显提高信道估计性能,降低计算复杂度,减少测量导频数目,提高系统容量.
1 系统模型
考虑NT根发送天线分布于不同地理位置,NR根接收天线集中于同一处地理位置的分布式MIMO-OFDM系统,其系统模型如图1所示.图中,虚线表示发射的信息符号经过前端处理后,到分布
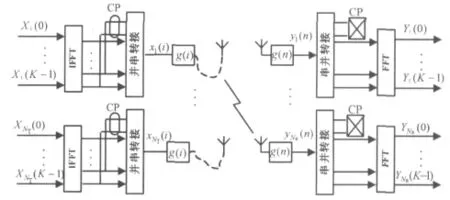
图1 分布式MIMO-OFDM系统模型

式中:Ex为总的发射功率;K为每根发送天线发射OFDM符号的子载波总数;bt(k)是第t根发射天线的第k个数据信息符号;g(i)为发送天线的基带波形;Ts是发送OFDM符号的周期.式发送天线的光纤或同轴线.假设i时刻第t根发射天线发送的OFDM符号用K×1维数据xt(i)表示,发送之前该数据经过离散傅里叶逆变换(IDFT)的快速算法(IFFT)处理.在快衰落环境下,为了有效对抗多径时延扩展,还需要在OFDM符号间加入循环前缀(CP)作为保护间隔,循环前缀需要大于信道冲击响应的最大抽头数,则第t根发送天线发送的数据可以表示为
2 分布式MIMO-OFDM系统快衰落信道估计
2.1 高速移动接收采样
在接收端高速移动环境下,发射信号经过快衰落信道后,接收端去除循环前缀,则第r根接收天线接收到的信号为
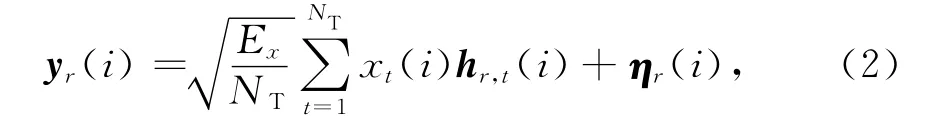
式中:hr,t(i)为发送天线t到接收天线r第i时刻分布式MIMO-OFDM快衰落信道矩阵;ηr(i)为接收天线r接收到的加性复高斯白噪声.由于接收端高速移动,分布于不同地理位置的发送天线经过各自时延到达接收端各个天线,因此,接收机接收到的信号可表示为
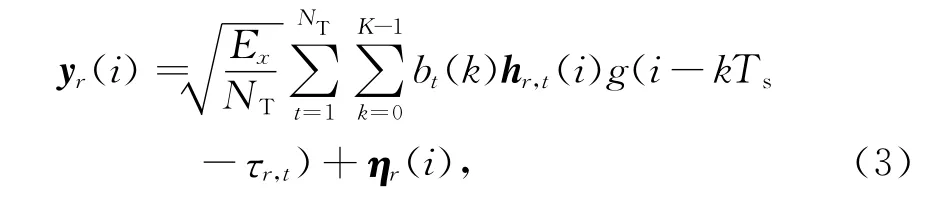
式中τr,t为发送天线t到接收天线r的信道传播时延.将第r根接收天线上的信号yr(i)通过匹配滤波器组,对不同发送天线到接收天线r的信号进行匹配滤波,可得接收信号通过发送天线j的匹配滤波器后n时刻的输出为

式中bt(n)为n时刻第t根发送天线发送的K 个数据符号而匹配滤波器组相关值为

式中符号(·)*表示复数共轭,通过匹配滤波器组加性复高斯白噪声相关矩阵ηr,j(n)=E{ηr(nTs)g*(iTs-τr,j)}.由式(4)可得到NT根发送天线到第r根接收天线上的信号为

式中:yr(n)=[yr,1(n),…,yr,NT(n)]T;Gr,t(n-i)=[Gr,t,1(n-i),…,Gr,t,NT(n-i)]T为分布式 MIMO-OFDM相关矩阵;符号(·)T表示矩阵转置.
2.2 三维互相关联合稀疏信道模型
在考虑分布式MIMO-OFDM接收情况时,为了便于分析,通常假设分布于不同位置的发送天线到达移动端接收天线的信道之间阴影衰落相互独立.然而当移动终端高速移动情况下,实际测量表明,各信道之间阴影衰落存在互相关性和干扰性,其与收发天线之间的距离、周围的环境和接收信号的到达角度有关[14].
因此,由式(6)可知,为了估计第n时刻第t根发送天线到第r根接收天线之间的信道冲激响应hr,t(n),利用分布式 MIMO-OFDM 系统快衰落信道间的感知数据在空间、时延和多普勒频移上的互相关性,获得信道的联合稀疏模型,进而将式(6)的信道冲激响应表示为
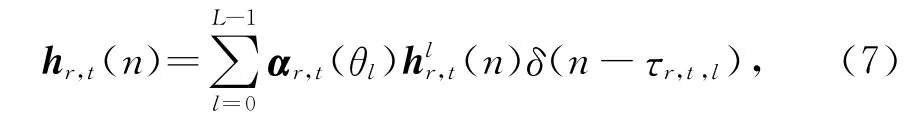
式中:τr,t,l发送天线t到接收天线r第l条径的时延扩展;L=[τmaxKΔf+1]为信道有效传播路径数,τmax为最大时延扩展,Δf=1/(KTs)为子载波频率间隔,Ts为采样间隔;hlr,t(n)为路径衰减;α(θl)=[1,exp(-jθl),…,exp(- (Mt-1)jθl)]T为阵列流形向量,θl=πsin(φl)(-π/2≤φl≤π/2,-π≤θl≤π),φl为第l条径波达方向(DOA),则发送天线t到接收天线r的第l条径信道冲激响应hlr,t(n)=[hlr,t(n,0),…,hlr,t(n,K-1)],进一步将hlr,t(n)表示为[14]
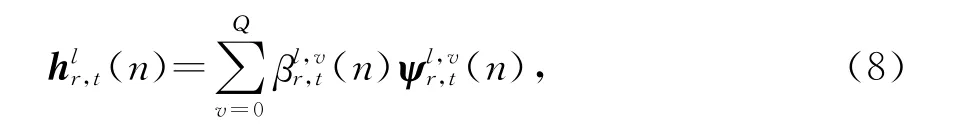
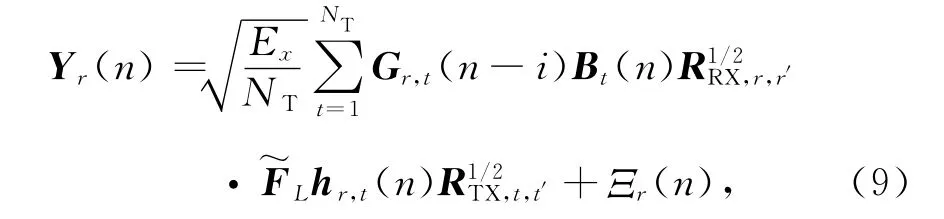

ρRX,r,r′表示第r根接收天线与第r′根接收天线之间的互相关系数,ρTX,t,t′表示第t根发送天线和第t′根发送天线之间的互相关系数.将式(7)和式(8)代入式(9)中,可得
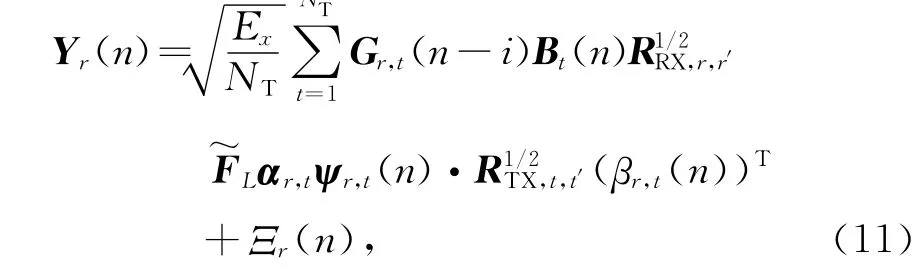
式中:αr,t=diag{αr,t(θ1),…,αr,t(θL)};Ψr,t(n)=[ψr0,t(n),…,ψrQ,t(n)]T.由式(7)可知,当发送天线t到接收天线r的第l条径稀疏分量 βlr,t(n)≤γ,信道系数稀疏分量可以忽略,进而发送天线t到接收天线r的L条径稀疏分量 βr,t(n)ℓ0≪KL(Q+1),其中γ为能量门限,ℓ0计算向量的非零数.因此,当时,分布式MIMO-OFDM快衰落信道在空间域、时延域和多普勒域就可以进行三维互相关联合稀疏,其稀疏度为S,而NTL⊗1维空间域矩阵为 [αr,1,…,αr,NT]T,NT(Q+1)⊗1维时延多普勒域矩阵为[ψr,1,…,ψr,NT]T.
2.3 分布式感知三维互相关联合压缩测量和重构
针对式(10),结合分布式压缩感知算法,对信道间稀疏冲激响应进行相关联合压缩和重构,而各发送天线预相关测量导频数需满足约束等距性(RIP)[15]条件,即Mt(n)≥ CS,其中C=(S+1)/S,Mt(n)为第t根发射天线在第n时刻导频数.导频符号取值为等概率的Bernoulli随机变量±1,预相关测量导频符号插入位置为:在发送端,同时在第n时刻,NT根发送天线中的每个OFDM符号的K个子载波中随机选取Mt(n)个子载波用于传输导频符号,其余K-Mt(n)个子载波用于传输用户数据.在接收端,为了互相关联合提取第n时刻各发送天线到第r根接收天线之间导频点上的接收信号Yrp(n),可以通过第n时刻第t根发射天线Mt(n)×K 预相关随机导频测量矩阵t(n)来获得,并且(n)矩阵随机选取导频位置和个数与发送端导频随机插入位置一致,矩阵t(n)在对应有导频位置的元素取值为1,其他没有对应导频位置的元素取值为零.由式(11),可得到n时刻NT根发送天线与第r根接收天线之间上的导频接收信号为

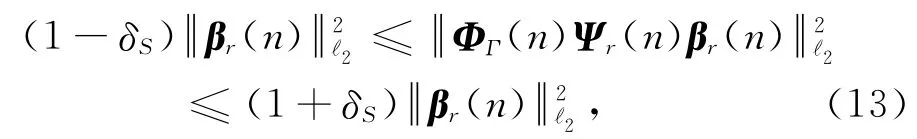
式中:|·|ℓ2表示ℓ2范数;ΦΓ(n),Γ⊂{1,…,NT}由Φr(n)的列向量构成;βr(n)=[βr,1(n),…,βr,NT(n)]T,Φr(n)=[Φr,1(n),…,Φr,NT(n)];Ψr(n)=diag{Ψr,1(n),…Ψr,NT(n)}.对所有子集Γ满足Γ ≤S,S稀疏向量βr(n)∈RΓ.由RIP条件可知,如果信道联合稀疏性越强,那么所需要的导频数将越少,也就大大地提高了系统的频谱利用率.进一步由式(12)可得
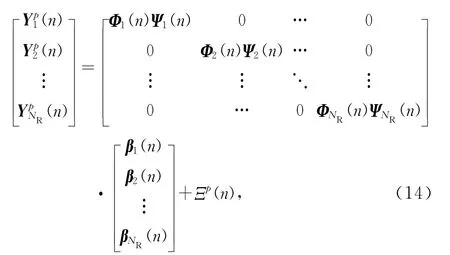
式中,Yp(n)=[Yp1(n),Yp2(n),…,YpNR(n)]T.由式(14)可知,NT根发送天线分布于不同地理位置,从不同发送天线到达NR根集中接收天线的快衰落信道有一定的随机性和相关性,每一根发送天线到达每一根接收天线的有效多径信号都存在于一定角域区域.而每条多径信号的时延扩展和多普勒频移都将分别局限于最大时延扩展和最大多普勒频移之间,因此每根天线角域内的信道系数是有限的,无线多径信道的冲激响应主要与少数主要路径的集合有关,大部分信道能量系数为零或者接近零,信道冲激响应在空间域、时延域和多普勒域具有互相关联合稀疏性.在相同来波角域内,冲激响应均匀分布时相关性最强,拉普拉斯分布时相关性次之,高斯分布时相关性最小.为重构式(14)中NT根发送天线到NR根接收天线的快衰落稀疏信道系数,需求解下式
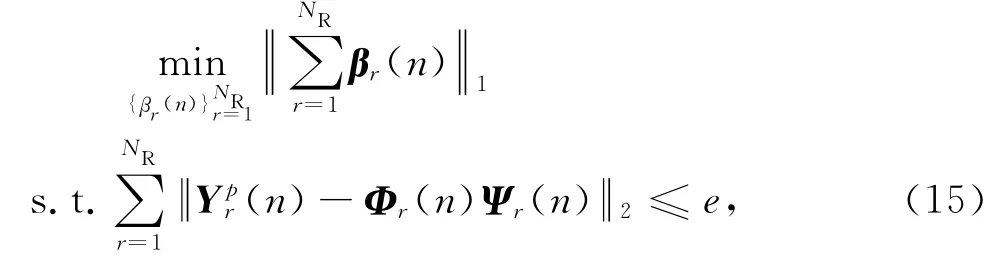
式中e与信噪比有关,为降低计算复杂度,准确快速求解式(15),结合分布式压缩感知算法,各接收端获得的测量信号采用共同的稀疏基,以能量有效的方式对信道间稀疏冲激响应进行联合重构,得到各接收端任意的稀疏信道系数,联合方法如下:
1)初始化接收导频信道迭代残差为

指示集 Ω(0)={},被选列向量Θ(0)=[],迭代次数统计j=1.
2)CΛ(j)为导频信道迭代残差与第Λ 个三维互相关联合快衰落稀疏信道基元素的NR×1维相关向量,其 中NTKL(Q+1)-(j-1),平均值为式中选择有共同最大内积残差的相关向量接收信号最大能量残差列指示
3)在候选集ζ(j)中搜索,最大限度地减少平均残为

式中(·)†矩阵伪逆.
5)更新接收导频信道残差为

6)在候选限制集中比较导频信道残差 rr(j)22和指示集Ω(j),如果候选限制集已经选择完,将返回到第2)步.
7)在联合稀疏基上获扩展系数,确定指示集Ω(j)中快衰落稀疏信道β(n)的非零系数,其值为


2.4 性能分析
采用分布式感知三维互相关联合压缩测量和重构方法,对信道冲激响应稀疏系数进行联合重构,可得r(n)满足

对于信道估计方法的计算复杂度,为了估计第n时刻第t根发送天线到第r根接收天线之间的KL(Q+1)信道响应矩阵hr,t(n),传统导频辅助的信道估计方法[5-7],通过对每根发送天线的接收信号分别插值的方法得到对应数据子载波上的频域冲击响应.采用此类方法,每根发送天线导频的插入比例需要满足奈奎斯特采样频率条件,推导了最优导频序列数为NRNTKL(Q+1).与传统信道估计方法不同,该方法并不需要先对每根发送天线的接收信号分别估计导频子载波点上的频域冲击响应,然后通过复杂的插值方法得到每根发送天线对应数据子载波上的频域冲击响应,而是先通过少量导频测量信号联合估计出少量的非零信道系数,然后通过三维互相关联合稀疏基就可以得到所有子载波上的频域冲击响应,因此大大减少了计算复杂度.
对于信道估计方法的传输效率和误码率,当采用压缩感知算法CS,每根接收天线快衰落信道重构概率分布为P≤1,所有接收天线快衰落信道的重构概率为PNT,因此必须通过增加导频数量和测量次数作为补偿,以便满足系统性能.为了解决这个问题,该文所采用分布式感知三维互相关联合压缩测量和重构方法,利用空间、时延和多普勒频移具有的互相关信息,对观测天线信道间感知数据进行联合重构,当导频观测次数为Mt(n)≥CS时就可以完全重构出信道冲激响应稀疏系数,可以获取更好的重构效果,由此可见,该文所采用方法能提高系统频谱效率和误码率.
3 实验结果分析
考虑收发天线皆为6的分布式MIMO-OFDM快衰落无线通信系统,6根发送天线分布于不同地理位置,6根接收天线集中于同一处地理位置.假设载波频率为5GHz的16-QAM信号,基带采样频率为5MHz,子载波个数为1 024,采样间隔TS为204.8μs,保护间隔为51.2μs.第r根和第r′根天线间相关系数可由下式得到
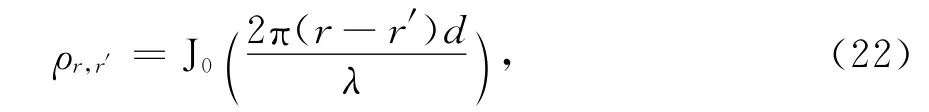
式中:J0(·)是第一类零阶贝赛尔函数;d是天线间距;λ是载波波长.相关系数第一个零点对应天线单元间距随着角度扩展增大而减小,且相关系数幅值随d增大而减小.接收端在城市和郊区环境下移动速度为250km/hr时,产生的最大多普勒频移为843.75Hz.高速运动的移动终端经历了随机多径衰落后,天线对之间的信号包络快衰落非常剧烈,最大衰落处达到几十分贝,这对移动终端接收机的正确接收判决影响十分严重.
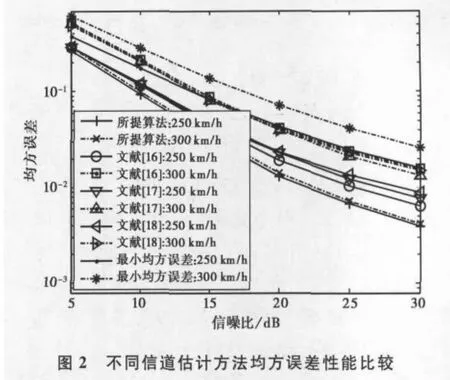
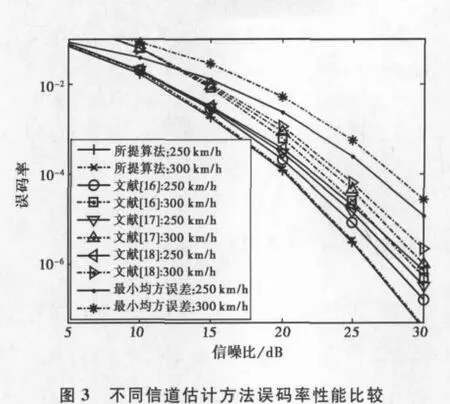
图2,3给出了各信道估计算法在不同信噪比(SNR)下均方误差(MSE)和误码率(BER)性能比较分析曲线.从图中可以明显看出,该文所采用方法的MSE和BER性能都要好于传统导频辅助线性最小均方误差(LMMSE)方法.LMMSE方法,每根发送天线的导频插入比例需要满足奈奎斯特采样频率条件.该文所采用方法并不需要先对每根发送天线接收信号分别估计导频子载波点上的频域冲击响应,然后通过复杂的插值方法得到每根发送天线对应数据子载波上的频域冲击响应,而是先通过少量导频测量信号联合估计出少量非零信道系数,然后通过三维互相关联合稀疏就可以得到所有子载波上的频域冲击响应,因此提高了均方误差和误码率.该文所采用方法的MSE和BER性能都要好于传统导频辅助的LMMSE方法,也好于文献[16]贪婪边界无状态路由(GPSR)方法、文献[17]启发式捻度(TWIST)方法和文献[18]匹配追踪(OMP)方法.特别是在快衰落程度越发严重情况下,当移动速度从250km/hr变化到300km/hr时,该文所采用方法与其他方法相比较,均方误差和误码率提高更加明显.因此,当采用现有算法,必须通过增加导频数量和测量次数作为补偿,以便满足系统性能;该文所采用分布式感知三维互相关联合压缩测量和重构方法,利用空间、时延和多普勒频移具有的互相关信息,对观测天线信道间感知数据进行联合重构,能提高系统频谱效率和误码率.
4 结 论
该算法降低了系统对导频的需求,提高了系统数据传输效率;减少了计算复杂度,提高了估计性能.针对传统快衰落分布式MIMO-OFDM系统中低数据传输效率,为了克服高速移动环境下快衰落干扰的弊端,考虑分布式 MIMO-OFDM快衰落信道间的感知数据,在空间、时延和多普勒频移上互相关联合稀疏模型,利用预相关随机导频测量矩阵,提出了基于分布式压缩感知理论的快衰落稀疏信道联合估计算法,得到各接收端任意地稀疏信道系数.仿真结果表明了所提估计算法具有较高频谱利用率和估计性能.
[1]SADJADPOUR H R,GARCIA-LUNA-ACENES J J.Capacity of distributed MIMO with finite size[C]//7th International Wireless Communications and Mobile Computing Conference,2011:1529-1534.
[2]VERDE F,DARSENA D,SCAGLIONE A.Cooperative randomized MIMO-OFDM downlink for multicell networks:design and analysis[J].IEEE Transactions on Signal Processing,2010,58(1):384-402.
[3]张晓燕,闻映红,谈振辉.陆地高速移动环境下电波传播特性的建模与分析[J].电波科学学报,2012,27(1):37-44.ZHANG Xiaoyan,WEN Yinghong,TAN Zhenhui.Simulation and analysis of radio wave characteristics in terrestrial high-speed mobile environment[J].Chinese Journal of Radio Science,2012,27(1):37-44.(in Chinese)
[4]李光球,陈素俊,余 晨.衰落信道上空频分组码的性能分析[J].电波科学学报,2012,27(3):440-446.LI Guangqiu,CHEN Sujun,YU Chen.Performance analysis of space-frequency block codes over fading channels[J].Chinese Journal of Radio Science,2012,27(3):440-446.(in Chinese)
[5]HLAING M,MUNOZ D.Pilot designs for channel estimation of MIMO OFDM systems with frequencydependent I/Q imbalances[J].IEEE Transactions on Communications,2010,58(8):2252-2264.
[6]HUNG K C,LIN D W.Pilot-based LMMSE channel estimation for OFDM systems with power-delay profile approximation[J].IEEE Transactions on Vehicular Technology,2010,59(1):150-159.
[7]AIDA Z,RIDHA B.LMMSE channel estimation for block-pilot insertion in OFDM systems under time varying conditions[C]//11th Mediterranean Microwave Symposium.Hammamet,September 8-10,2011:223-228.
[8]SHARP M,SCAGLIONE A.useful performance metric for compressed channel sensing[J].IEEE Transactions on signal processing,2011,59(6):2982-2988.
[9]ROMBERG J.Imaging via compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):14-20.
[10]TAUBOCK G,HLAWATSCH F,EIWEN D,et al.Compressive estimation of doubly selective channels in multicarrier systems:leakage effects and sparsity-enhancing processing[J].Selected Topics in Signal Processing,2010,4(2):255-271.
[11]EIWEN D,TAUBOCK G,HLAWATSCH F,et al..Multichannel-compressive estimation of doubly selective channels in MIMO-OFDM systems:Exploiting and enhancing joint sparsity[C]//IEEE International Conference on Acoustics Speech and Signal Processing,2010,14:3082-3085.
[12]BAJWA W U,SAYEED A,NOWAK R.Sparse multipath channels:modeling and estimation[C]//13th IEEE Digital Signal Processing Workshop.Macro Island,January 4-7,2009:320-325.
[13]BAJWA W U,HAUPT J,SAYEED A M,et al..Compressed channel sensing:a new approach to estimating sparse multipath channels[C]//IEEE Proceedings,2010,6(98):1058-1076.
[14]周小平,方 勇,汪 敏.MIMO-OFDM快衰落信道压缩感知估计方法[J].电波科学学报,2010,25(6):1109-1115.ZHOU Xiaoping,FANG Yong,WANG Min.Compressed sensing estimation methods for fast fading channel of MIMO-OFDM systems[J].Chinese Journal of Radio Science,2010,25(6):1109-1115.(in Chinese)
[15]HAUPT J,BAJWA W U,RAZ G,et al.Toeplitz compressed sensing matrices with applications to sparse channel estimation[J].IEEE Transactions on Information Theory,2010,11(56):5862-5875.
[16]SHANMUGA R B,PRABAKARA N,SARMA V R.Modified GPSR based optimal routing algorithm for reliable communication in WSNs[J].International Devices and Communications,2011:1-5.
[17]PORTILLA J,GIL-RODRIGO E,COND Y.Ultra-Fast high performance restoration using multi-frame[C]//18th IEEE International Conference on Image Processing,2011:1837-1840.
[18]CAI T T,WANG L.Orthogonal matching pursuit for sparse signal recovery with noise[J].IEEE Transaction on Information Theory,2011,57(7):4680-4688.

