圆环电流/荷在轴线上的磁/电场的两个简洁公式

周国全

（武汉大学物理科学与技术学院物理系，湖北 武汉 430072）

1 引言

在电磁场理论中，均匀分布的环状电荷在其中心轴线上任意一点的静电场，以及环形恒定电流在其中心轴线上任意一点的磁场，这两个典型问题，在几乎任何一本电磁学或大学物理教材中均为经典的例题或习题［1～6］，其结果表达式均显繁锁，难于记忆，不便应用.文献［7］通过引进立体角的概念，给出了这类问题的一种简洁表达式.本文推导出这类问题的一种简洁紧凑，易于记忆的三角函数表达形式，并将其罗列对比，以飨同仁.

2 圆环电流在轴线上任意一点的磁场

如图1所示，半径为R 的环形通有恒定电流I，在其中心轴线上到圆心距离为x 的任意一点P的磁感应强度B 可运用毕奥－萨伐尔定律加以计算，结果为［1，2］

其 中，μ0为 真 空 磁 导 率，i 为x 方 向 单 位矢量.

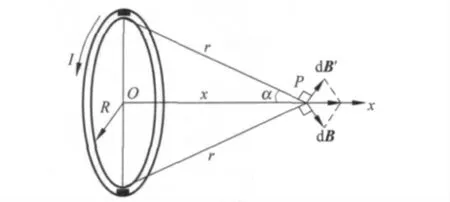
图1 圆环电流在轴线上的磁场

当x＝0时，式（1）表示的即是圆心O 点的磁感应强度BO，记为

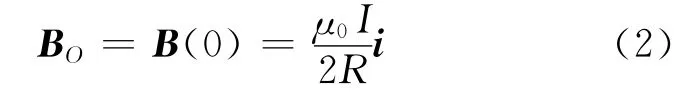
圆环上任意一点与P 点的连线即圆环为底面以P为顶点的锥体的母线，它与锥轴（x 轴）的夹角为α，易知

则表达式（1）可改写为如下形式

可记为

它显然形式简洁，易于记忆，便于应用.仅举以下两例说明.

1）运用式（4）与式（2），很容易证明，对于轴线上从左端无穷远到右端无穷远的唯一的一条不闭合的磁场线，安培环路定理依然成立.因为x＝Rcotα，所以如下积分易如反掌

2）如图2所示，圆台的侧面分布有均匀的环绕面电流，面电流密度为η；两圆形底面的半径分别为R1与R2.则其锥形侧面的圆锥顶点P 处的磁感应强度可如下算出：

图2 锥形圆台侧面环绕面电流在圆台锥顶点的磁场

由式（2）并代入以上二式可得

运用公式（4），并将式（6）代入可得

3 均匀圆环电荷在轴线上任意一点的电场

无独有偶的是，静电场中也有类似的问题.如图3所示，半径为R 的圆环带有均匀线分布的电荷，总电量为q.则其中心轴线上到圆心距离为x的任意一点P 的电场强度E 可应用库仑定律和微积分算出为如下公式

图3 圆环电荷在轴线上的电场

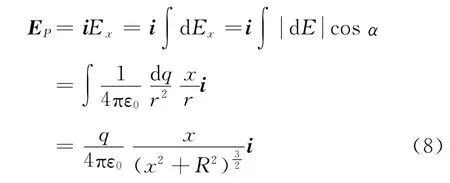
其中EPoint＝E∞即为x≫R 时的点电荷近似的理想结果，亦即将全部电荷视为集中于圆心的点电荷时电场强度的表达式.公式（9）与公式（4）比较，相映成趣，有着几分神似，便于对照记忆，因而在多年的教学实践中深受同学们的喜欢.公式（9）的应用举例如下.要计算一个无限大均匀带电平板附近任意一点的电场，我们先计算具有均匀面电荷分布σ，内外半径分别为为R1与R2的环状圆盘在其轴线上距离圆心为x 处的电场强度.如图4所示，

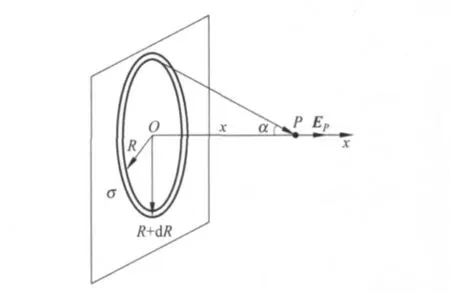
图4 无限大均匀带电平面的电场

其中，α1，α2分别是圆盘内外圆周对轴上点P 所张的锥面顶角之半.

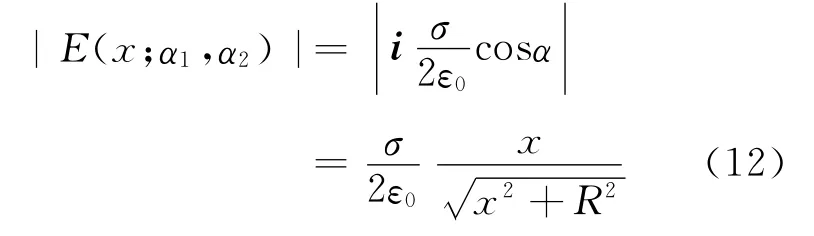
结果表明，场强与P 点坐标x 无关，因而无限大均匀带电平面两侧均为匀强电场.

4 结语

具有同样环状分布的电流的磁场（轴线上）BP＝BOsin3α 与 电 荷 的 电 场（轴 线 上）EP＝E∞cos3α的表达式之间，既有着如此惊人而美妙的相似之处，又有着本质特性的不同.这种情形在电磁场理论中并不鲜见，例如在有限或无限长直线电荷/流分布的电/磁场的表达式之间，也有着同样奇妙的相似与不同之处；又如电偶极子的电势与磁偶极子的磁标势之间的相似表达方式［3～6］，凡此种种，不一而足.其本质原因在于决定点电荷电场的库仑定律具有平方反比特性，且电场是一极矢，而元电流的磁感强度也具有平方反比特性，但磁场为一轴矢.这决定了电场与磁场两者之间在空间分布上的神似与不同之处.

［1］赵凯华，陈熙谋.新概念物理《电磁学》［M］.北京：高等教育出版社，2003第二版.42；96～97

［2］张三慧，臧庚媛，华基美.《电磁场》［M］.北京：清华大学出版社，1991第一版.17～19；229～230

［3］虞国寅，周国全.电动力学［M］.武汉：武汉大学出版社.2008第一版.74，88

［4］张之翔，王书仁，陈献伟.电动力学［M］.1988第一版.130～145；362～364

［5］俎栋林.电动力学［M］.北京：清华大学出版社，2006 第一版.109，96～97

［6］蔡圣善，朱耘.经典电动力学［M］.上海：复旦大学出版社，1985第一版.187～190

［7］佘守宪.立体角概念在电磁学中的应用.物理与工程，2004，14（2），5～11