圆柱形磁铁在金属管中的下落时间

黄志雷 王 越

（清华大学，北京 100084）

1 引言

磁铁在金属管中，因为电磁感应而慢速下落的实验，是电磁学课程中一个经典的演示实验.这个过程的物理图像是磁铁下落在金属管中产生感生电流，由楞次定律可知这个感生电流会阻碍磁铁下落.虽然定性分析比较简单，但是鲜有人对这个过程进行定量分析.本文希望从理论上，利用磁铁、金属管的各参数，对这个问题进行理论计算，并与实验结果进行比较，将电磁学教科书上的知识应用到实际问题中.

2 理论计算

经观察，在金属管内壁半径略大于圆柱磁铁半径的情况下，磁铁在金属管中下落时，很快达到恒定速度，保持该速度匀速下落.并且在下落时，磁铁基本保持竖直，与金属管共轴，即两圆形表面平行于水平面，圆心与金属管中心重合.因此，计算磁铁在金属管中竖直、匀速下落的速度，便可求得其在金属管中的下落时间.

磁铁周围有一个磁场分布，当磁铁以一定速度运动时，根据该磁场分布和速度，可以求得金属管中的电流.而金属管中的电流又会产生磁场，该磁场与磁铁作用，对磁场下落产生阻力.当该阻力与磁铁所受重力相等时，磁铁在金属管中匀速运动，此状态即为所求.这里忽略了金属管中电流产生的磁场的变化对金属管中电流的影响.使用上述思路对磁铁在金属管中下落问题进行研究比较繁琐，在计算时需要计算多次积分.从能量角度可以将计算简化.当磁铁匀速下落时，重力对磁铁做功，重力势能减少.由于磁铁是匀速下落，因此重力势能全部转化为金属管中电流产生的焦耳热.当焦耳热的热功率与重力所做功的功率相等时，便是磁铁匀速下落的状态.

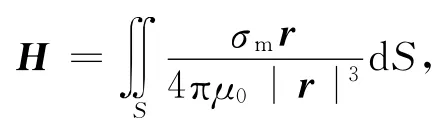
计算出磁场分布后，可以进而计算磁铁运动时，在金属管中产生的电流.可以将金属管看作许多金属圆环叠在一起.由于整个系统具有轴对称性，因此金属圆环之间没有电流.每个金属环产生的电动势可以根据磁铁产生的径向磁场和磁铁下落速度进行计算.当金属管管壁厚度相对金属管半径非常小时，可以近似认为金属环外径和内径中点所处点的磁场径向分量，就是整个金属环上每一点磁场径向分量.

图1 各物理量方向及位置示意图

3 理论结果与实验结果对比

对磁铁在金属管中的下落时间进行实际测量.实验中所用圆柱形磁铁直径（13.97±0.02）mm，高（10.00±0.01）mm，剩磁（1.21±0.03）T，这些为磁铁的已知参数.实验使用3根长约1m，半径约9mm，管壁厚度约2mm 的金属管.材质分别为黄铜、紫铜和铝.本实验中，除了金属管电阻率外，其余物理量都比较容易测量.本实验使用四点法测量金属管电阻，再依据金属的形状，得到金属的电阻率.测量时，先用砂纸将金属管两端外层的氧化层打磨掉，再用铜箔进行包裹作为电极.测量时，两端接入电流从－1A 变化到1A，得到电压和电流的关系后进行线性拟合，进而得到金属管的电阻.图2是测量黄铜管电阻的数据的拟合图.得到的不同金属管的电阻和电阻率如表1.

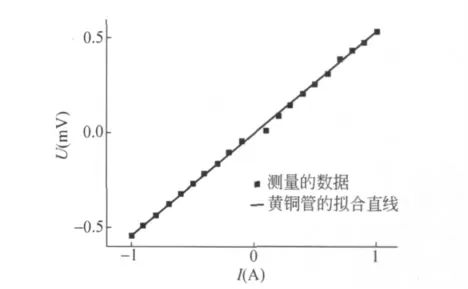
图2 测量黄铜管电阻的数据和拟合直线

表1 不同金属管的电阻和电阻率

表2为磁铁下落的理论时间与实际测量时间的对比，从中可以看出，该计算结果具有较高的精确度.这也可以说明，理论计算所做的抽象模型和假设是较为合理的.

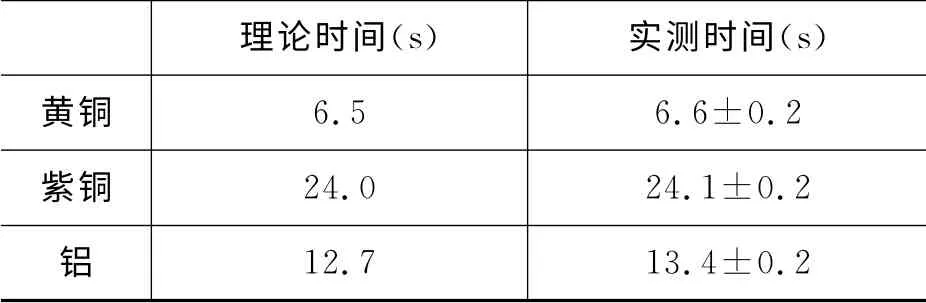
表2 磁铁下落的理论计算的时间与实际测量时间的对比

下面对结果进行简要的分析和讨论.从表2中可以看出，铝的下落时间的理论值和实验值之差明显大于另外两种金属管.这是由于铝的电阻率的测量有较大误差.铝在空气中会迅速氧化，使得在打磨之后，铝的表面依旧会出现对测量产生较大影响的氧化层.这意味着测量的电阻率要比实际电阻率大，计算的下落时间小于实验测量时间，与结果在趋势上相符.

还可以对磁铁在金属管中加速下落的时间进行粗略估计.金属管中电流正比于磁铁下落速度，磁铁受到的阻力正比于电流.这样磁铁加速度与速度是线性关系，即a＝g－kv，g 是重力加速度，k为一常比例系数.这样，下落速度的形式为vs（1－et/τ），其中vs是稳定速度，时间常数τ＝vs/g 反映加速运动时间.以紫铜为例，τ≈4ms，这意味着在当前测量精度下，加速下落过程确实可以忽略不计.

4 小结

理论上用磁荷法计算得到磁铁磁场分布，进而得到磁铁在金属管中下落时间，与实验测量的结果相符.从开始的理论建模到之后的具体计算、与实验结果比较，这个过程将电磁学书籍中理想的理论公式应用到了具体的物理现象中.这个现象还存在一定的应用价值.比如磁铁的剩磁是比较难测量的物理参数，在已知金属管电阻率的情况下，可以利用这种方法对其进行测量.类似的，在已知磁铁剩磁的情况下，可以对导体棒的电阻率进行测量，特别是如果导体棒的横向电阻与纵向电阻不一致时，这种方法可以测量难以测量的横向电阻.

［1］胡友秋，程福臻，叶邦角.电磁学与电动力学 上册［M］.北京：科学出版社，2008，176～181

［2］梁灿彬等.电磁学 2 版［M］.北京：高等教育出版社，2004.303～307