在普物教学中用守恒量研究开普勒运动的一点补记

李 力

（重庆清华中学，重庆 400054）

在普物教学中用守恒量研究开普勒运动的一点补记

李 力

（重庆清华中学，重庆 400054）

针对开普勒运动中三个守恒量之间的关系，给出两种适合普通物理教学的证明方法，并指出一种用守恒量完整研究开普勒运动的普物教学思路.

开普勒运动；守恒量；普物教学

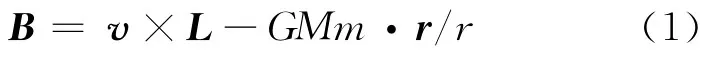
目前，已有一些普物教材用三个守恒量讲解开普勒运动，优点是数学推导较简单，不须解微分方程和积分运算，物理意义也非常鲜明，很适合普通物理层次的教学.比如在文献［1］中，通过计算径矢与矢量B的标积r·B便得出了行星轨道的极坐标方程［1］

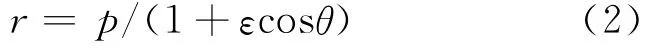
其中

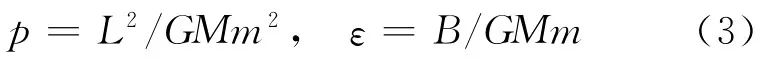
由此可知行星轨道是圆锥曲线，ε是偏心率，p是半正焦弦.这样可以看出矢量B的几何意义：其方向沿通过焦点的对称轴，指向最近的拱点，其大小正比于偏心率［1］.

但文献［1］接下来转而用有效势能曲线研究开普勒运动，只得到椭圆轨道情况下的公式［1］

其实上面这个公式可一般地写为

式（5）表明了能量与行星轨道形状之间的重要关系，对抛物线轨道（E＝0，ε＝1）、双曲线轨道（E＞0，ε＞1）和椭圆轨道（E＜0，ε＜1）的所有情况全部适用.

实际上在推出轨道方程（2）后，再导出守恒量L、E、B之间的关系，可以直接得到用能量表示圆锥曲线轨道种类的普遍公式（5），这是用三个守恒量完整解决开普勒运动的一种有效的普物教学思路.为此，我们先用两种适合普物教学的证明方法推出三个守恒量的关系.

由于是守恒量，故可以用拱点这个特殊点来计算，不难发现在拱点上，r，v，L三者成两两垂直的空间关系，且v×L与r同向，所以有

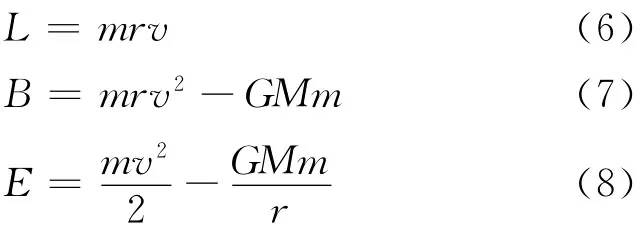
从式（6）、（7）得v＝（B＋GMm）/L 和r＝L2/［m（B＋GMm）］，均代入式（8），化简得

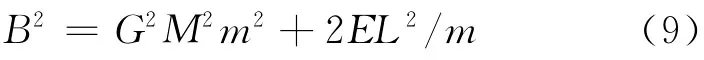
这就是开普勒运动中三个守恒量之间满足的关系式.还可以将式（1）与自身点乘，得

最后，把式（9）代入式（3）中后一个式子，便得到式（5）.这样用三个守恒量不但导出了行星运动的轨道方程，而且也推出了决定轨道形状的公式，完整地解决了开普勒运动.

［1］ 赵凯华，罗蔚茵.新概念物理教程（力学，第二版）［M］.北京：高等教育出版社，2004.330，331，332

2012－05－02）