混沌实验教学之路
张连芳 傅敏学 刘滢滢 高 红 柯伟平
(清华大学物理系,北京 100084)
混沌研究是20世纪物理学的重大事件.物理学对于不同的自然现象,如天体运动、布朗运动等,分别用确定论和概率论两套不同的理论体系来描述,两种体系在认识论上是对立的.作为非线性科学研究最重要的成果之一,混沌研究缩小了两个体系的鸿沟.混沌研究表明,一个完全确定的系统,即使非常简单,但由于自身的非线性作用,同样具有内在随机性.混沌既不是具有周期性和对称性的有序,又不是绝对无序,而是可用奇怪吸引子等来描述的复杂有序——混沌呈现非周期有序性.
为了在物理实验课程中增加非线性的内容,自2002年起,我们开设了混沌电路实验.随着实验的深入和多次改型,我们坚持用分立元件与学生自组的实验方案,坚持理论与实验过程相结合.现在混沌电路实验包括非线性元件电阻、电感或电容的选择,倍周期分岔产生混沌的过程,混沌吸引子、电路波形和频谱分析图等混沌状态显示,计算机模拟混沌吸引子的演化过程等内容,成为一个颇有趣味的非线性实验.
1 混沌的研究方法
混沌研究从非线性动力学方程y=ax2+bx+c 开始,写成参量方程
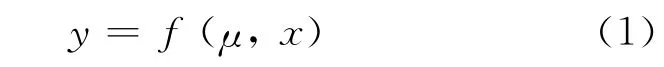
其中,μ(a,b,c)为参量集合;x 方次为2即是抛物线方程.研究方程随时间t演化即为一阶自治差分方程
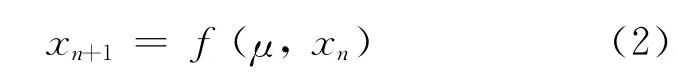
下一时刻的xn+1状态取决于方程参数和当前状态xn.方程(2)的一种标准形式为
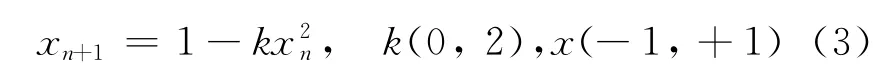
方程(3)包含了混沌的主要特征[1].研究xn随k的演化过程用倍周期分岔图(图1)来表示,显示了系统从稳定轨道经过倍周期分岔进入混沌的途径,而且在混沌带中呈现了新的周期窗口和自相似的分岔图等复杂结构.
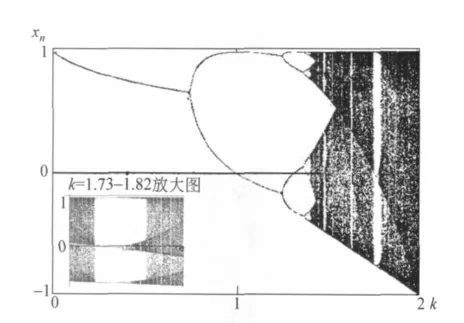
图1 混沌演化的分岔图
2 非线性电路中的混沌
研究非线性混沌电路,分析电路特性和产生周期、非周期振荡的条件,可以了解混沌产生的方法和混沌现象的基本性质.
一个简单而典型的非线性混沌电路如图2,它又称蔡氏电路(Chua's circuit),即三阶互易非线性自治电路.其中的非线性元件是电阻RN(g=1/RN),且呈现负阻性.L 和C2组成无损耗振荡电路作为振荡源.耦合电阻G(实际是电导)呈现正阻性,它与非线性电阻RN和电容C1组成耦合电路消耗能量,以防止由于非线性电路的负阻效应使电路中的电压与电流不断增大.
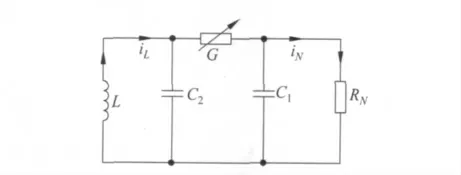
图2 蔡氏混沌电路原理图
电路的状态方程式(即电路中节点或支路的电流、电压关系式)为
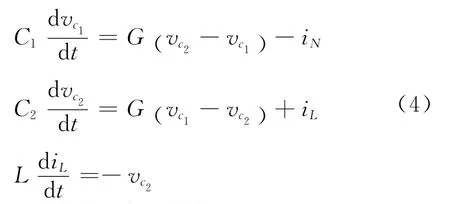
其中,iN是非线性电阻RN上的电流.
图2电路中的非线性元件为RN,是具有分段线性的负阻器件,其特性见图3,数学表达式合式为
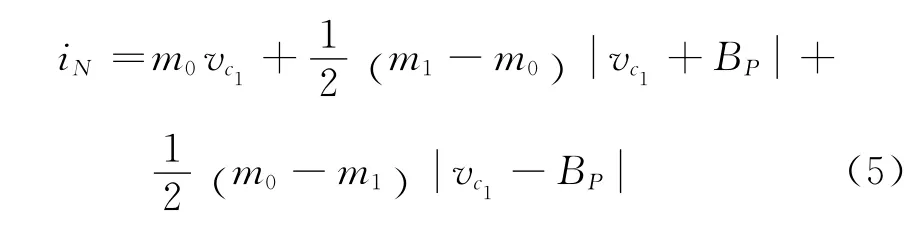
实验中用于产生非线性电阻的方法很多,如单结晶体管、变容二极管以及运算放大电路等.最初蔡氏方案选用单一运放电路作为非线性元件的电路,俗称蔡氏二极管[2].为了方便调整,电路很快改为图4的双运放电路[3],其伏安特性与图3相似.实验时,只需改变耦合电阻G,电路即可从稳定周期振荡过渡到混沌状态.蔡氏电路的混沌状态,呈现出两个无限多次循环的层状结构以螺旋形式相互卷在一起,称为双漩结构(double scroll).具有双漩结构的吸引子称为双漩吸引子.将VC1-VC2信号输入示波器x-y 轴可观察双漩结构,图5表示改变G 的值,相图VC1-VC2从单周期P,倍周期2P,4P,……单漩……3P……双漩进入混沌的过程,这种过程与第一节的理论分析是一致的.
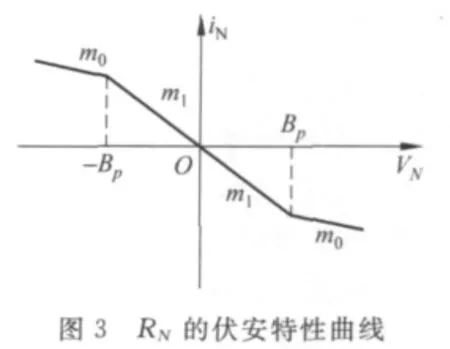

图5 从倍周期分岔到双漩吸引子
3 混沌电路实验的扩展内容
3.1 非线性电阻RN 伏安特性的测量
RN的特性对混沌电路非常重要.在非线性电阻输出端接入可变电阻和电压表与电流表,可直接测量iR<0区域RN的非线性伏安特性,各线段分段拟合后得

测量表明,这种电路在分段线性方面要求与混沌电路要求的理论特性相近.但是U 过大或过小时都出现了负阻向正阻的转折,这是运算放大器进入饱和区的输出现象,这个特性导致在电路中产生附加的周期轨道,对产生混沌吸引子和倍周期分岔轨道没有影响.
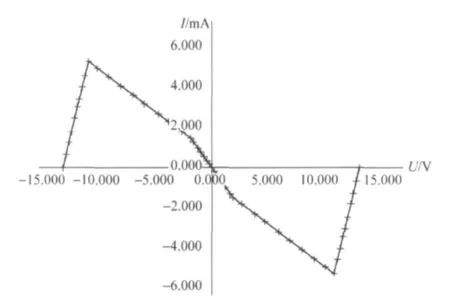
图6 双运放RN 的实验I—V 曲线
具有电路分析技能的实验者也能从运放电路的参数分析得到电路输出的伏安特性.根据运放的型号TL-082和输出Swing电压为±13V 等参数可得到与I1、I2基本相同的关系式,但I3差别比较明显.具体原因可能是运放参数Swing电压不一定准确或者别的未知因素.好在这段参数对产生混沌轨道没有影响,暂时未做深究.
3.2 混沌电路的变化
电路中产生混沌现象的必要条件是电路中具有非线性器件,这种非线性器件可以是变容二极管(电容是端电压的非线性函数),带磁芯的电感或互感,非线性电阻等.电感变化产生的混沌电路如图7,L2和C2用来产生混沌现象的振荡电路[4].电感线圈共有三个绕组,L0用于直流激磁,L1、L2为互感线圈,互感量为M.
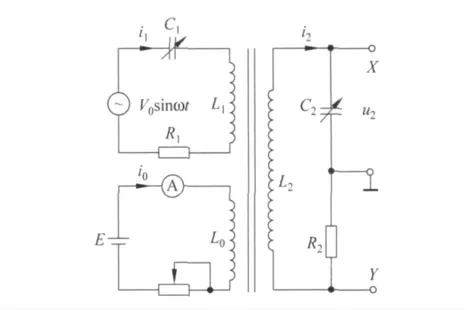
图7 带电感的混沌电路
在i0一定条件下,电路方程是以i1、i2,u2为变量的三阶方程.电路方程为
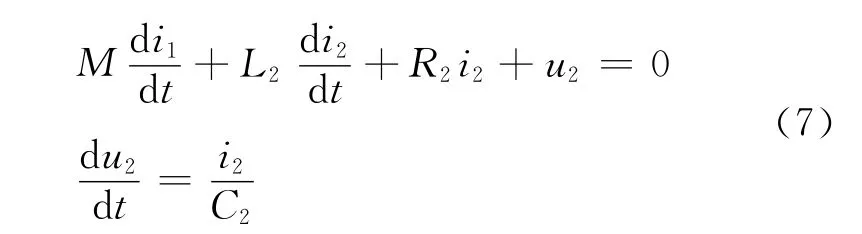
改变电感的参数,能够实现电路从倍周期分岔,即从基频(1P),二分频(2P),四分频(4P),八分频(8P)……进入混沌状态的过程.实验中也可观察到在混沌带复杂的区域中部出现正规的周期窗口的过程.改变L0中电流、改变信号源V0sinωt幅值V0、改变信号源角频率ω 等多种途径都可以实现混沌过程.
3.3 蔡氏混沌电路的计算机模拟
从前面分析可以看出,蔡氏电路是一个三阶非线性自治电路,而混沌过程是电路随时间演化达到某种约束的稳定或非稳定状态.计算机模拟对这样的过程是容易实现的.我们用Mathematica编写的程序可以模拟蔡氏电路方程的状态,输入L1,C1,R(R=1/G)与RN的参数m0、m1、BP,就可以得到蔡氏电路的iL-uC2,uC1-uC2,iL-uC1的相图和u1的波形图,图8用程序模拟了电路中波形变化及双漩吸引子形成的过程.模拟程序也为正确选择电路参数提供了分析的手段.
值得注意的是对蔡氏电路及其吸引子的研究已成为一种检验电路行为的诊断程序,Bilotta E,Pantano P[5]等用实验电路和计算机模拟等手段得到几百种蔡氏电路的吸引子,形成了令人叹为观止的吸引子博物馆,为电路研究和混沌现象提供了庞大的案例.这样的案例可能不是混沌电路研究完全必要的,但已成为电路和混沌现象研究的重要路径.正如计算机对圆周率π的计算已达几百位小数并不是现实世界的必需,而是检验计算机能力的一种重要判据.
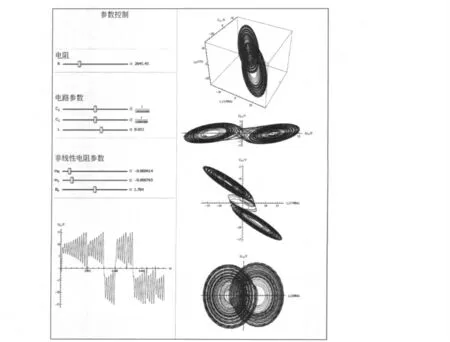
图8 程序模拟的蔡氏电路状态图
多年来混沌实验的教学之路使我们感悟到:实验是发现、检验和解决理论问题的基本和权威路径,要重视用实验解决问题的方法和能力;实验提供了丰富多彩的知识和技术,而实验设计者一定要具备宽厚的理论知识,熟悉和掌握现代的技术工具.
[1]郝柏林.从抛物线谈起——混沌动力学引论[M].上海:上海科教出版社,1995.1~35
[2]T.Matsumoto et al.,The Double Scroll(Part Ⅰ),IEEE Transaction on Circuits and Systems,Vol.CAS-32,1985,798~804
[3]王珂,田真,陆申龙.非线性电路混沌现象实验装置的研究[J].实验室研究与探索,1999,(4)
[4]曹惠贤,李蓉等.普通物理实验教程[M].北京:北京师范大学出版社,2007.302~309
[5]Bilotta E,Pantano P,Stranges S..A gallery of Chua attractors:Part I,International Journal of Bifurcation and Chaos.2007,17(1):1~60

