变倍光学系统的公差分析＊

刘雨沁，张孟伟

（中国科学院 光电技术研究所，四川 成都 610209）

引 言

电视搜索跟踪一体化系统一般具有两个或者两个以上视场，大视场搜索，小视场精确跟踪，根据系统搜索／跟踪的具体要求，在两个视场中切换［1］。在变倍光学系统的理论设计中，设计的性能不包括任何类型误差的影响，而与实际设备有关的制造误差和装配误差往往降低成像质量，并且由其造成的像质下降经常是设计像差造成像质下降的许多倍。因此根据成像要求，选择适当的加工工艺，合理分配制造公差和装配公差，确保加工出来的实际系统能够达到成像要求就显得十分重要。

1 变倍光学系统及性能指标

变倍光学系统如图1所示，光学系统由物镜组，场镜组，调焦组和变倍组构成，调焦组前后移动使一次像面处于其焦点处，变倍组整体切换实现系统焦距在300～600mm 之间的变换。

光学设计性能指标如表1所示，要求中心视场无明显球差、彗差、像散及色散。对于照相物镜，光学传递函数评价像质已被广泛接受［2］，利用光学传递函数可以很直观、很明了地反映镜头在加工和装校中存在的问题［3］。因此为了利用单一指标衡量各种光机公差对像质的影响，选用各个视场下二分之一奈奎斯特频率处弧矢方向和子午方向的光学传递函数（MTF）的平均值作为目标函数，CCD 像素尺寸为7.4 μm，二分之一奈奎斯特频率为34lp／mm。变倍光学系统MTF 曲线如图2 所示，在两种焦距状态下，目标函数的值分别为0.778 和0.614。

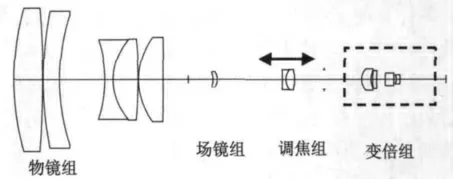
图1 变倍光学系统Fig.1 Switch－in－group zoom optical system

表1 光学设计参数Tab.1 Optical parameters

图2 调制传递函数Fig.2 Modulation transfer function

2 系统公差分析

2.1 公差等级和公差计算

公差等级如表2所示，被认为适用于大多光机系统［4－5］，8组公差等级（Q1～Q8）分别代表着不同的加工水平和加工难度。其中Q1接近于加工极限，而Q8则代表最差的加工水平。

表2 公差等级Tab.2 Tolerance Grades

公差计算的流程图如图3所示，8组公差等级依次输入Zemax光学软件，并选择后焦距作为补偿环节，进行1 000次蒙特卡罗模拟，最后输出目标函数的下降量和满足成像要求的基本公差等级。选择后焦距作为补偿是因为在最后的测试和装配期间，光学系统需要被重新调焦，所以这个选择是合理的。

2.2 光机参数灵敏度分析

若目标函数与结构参数的函数表达式为：

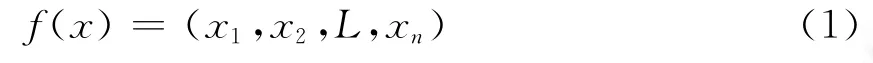
结构参数在名义值四周的微小变化所引起的目标函数变化为：假设各参数之间相互独立，则［6］：

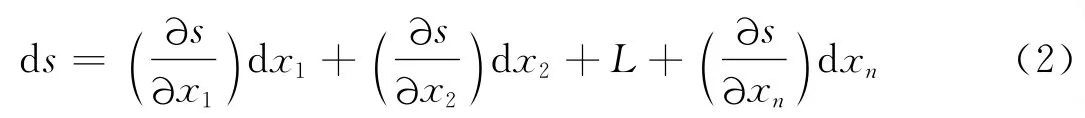
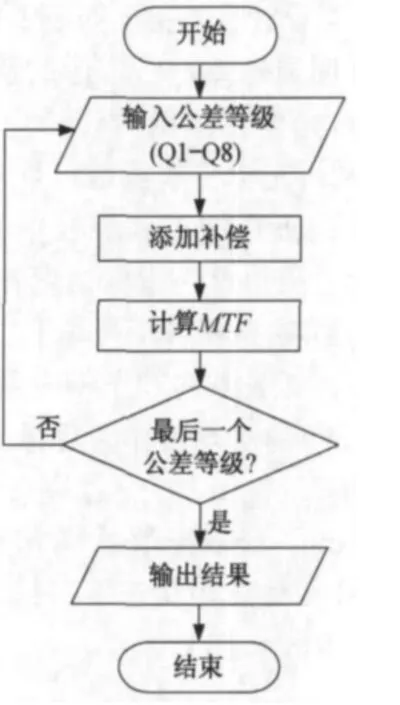
图3 公差计算流程图Fig.3 Tolerance calculation flow chart

其中，Ts为目标函数的下降量，为了综合由多个参数引起的性能下降，将多个参数造成目标函数下降量平方和的均方根作为目标函数的下降量。参数灵敏度∂s／∂x 表示目标函数随单一参数微量变化的变化率，且当像差校正到最佳状态时，目标函数随单一参数微量变化的曲线可看成近似对称抛物线，因此分析时选用抛物线的一侧，进行一次曲线最小二乘法拟合，取其斜率作为灵敏度的衡量标准。由于各类公差之间的量纲不一致，且不同公差种类参数的概率统计分布也不一样，因此曲线的斜率只能代表同类公差中不同位置参数的灵敏度，而对于各类参数之间的灵敏度，将其统一到同一公差等级，考虑到实际加工误差的随机性，采用多次蒙特卡罗模拟，取目标函数下降量的平均值作为参数间灵敏度的衡量标准。

2.3 公差分配

在基本公差等级下，对同类公差中不同位置的公差进行公差分配。若认为参数是等概率作用于目标函数，式（3）右边各项相等，则各参数公差为：

通过式（4）解得的参数公差Txj存在过宽的情况，因此需要根据参数灵敏度和基本公差等级调整权重，使各参数公差都接近于基本公差等级。将Txj与基本公差等级比较，取其比值为权重。设Wj第j 个参数的权，则式（3）变化为：

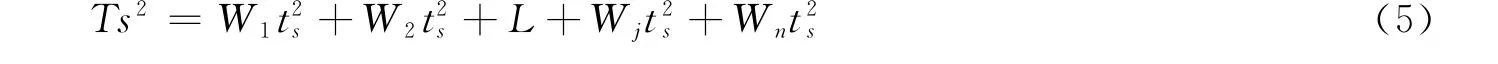
因此，各参数公差为：

3 优化结果分析

依次对两种焦距状态进行公差计算，结果如图4所示，对于短焦组，Q1～Q5满足设计要求，对于长焦组，Q1～Q3满足设计要求。因此，选择Q3 为基本公差等级，在基本公差等级下的目标函数值分别为0.614 3和0.312 2。

参数灵敏度如图5所示，制造公差为折射率公差、阿贝公差、厚度公差、透镜楔角公差、表面不规则度公差和光圈公差，装配公差为透镜位置公差、透镜偏心公差、透镜倾斜公差、镜组位置公差、镜组倾斜公差和镜组偏心公差。参数公差中，折射率公差、厚度公差、光圈公差、透镜位置公差和透镜偏心公差为敏感公差，选择敏感公差进行公差分配，下面以厚度公差和透镜位置公差为例列出计算过程和结果。

对于变倍光学系统，共用光路的厚度公差和透镜位置公差的灵敏度如图6所示，横坐标分别代表透镜编号和透镜之间的距离编号。可以看出，两种焦距状态下共用光路的灵敏度大致相同，因此，可以选择短焦距进行公差分配，结果也同样适用于长焦距状态。

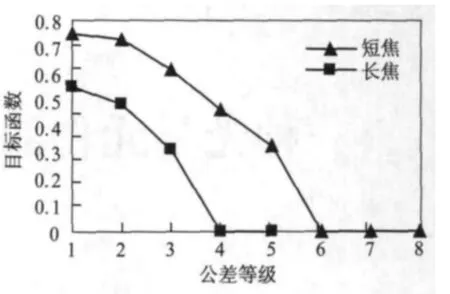
图4 各个公差等级下的像质退化Fig.4 Image quality degradation of different tolerances

图5 参数灵敏度Fig.5 Parameters sensitivity

图6 共用光路灵敏度Fig.6 Public optical path sensitivity

在Q3公差等级下，透镜厚度公差和透镜位置公差对应的目标函数公差Ts 分别为0.344 2和0.136 4，初始公差值由基本公差等级决定，利用式（6）计算出优化公差值。

灵敏度系数（厚度）：0.122，0.482，0.023，0.044，0.149，0.377，0.069，0.041，0.399，1.185，0.088，0.012；

初始值（厚度）：0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5；

优化值（Tx）：0.03，0.02，0.07，0.05，0.025，0.02，0.04，0.05，0.01，0.01，0.04，0.09；

灵敏度系数（位置）：0.009，0.231，0.231，0.064，0.002，0.002，0.018，4.221，0.303；

初始值（位置）：0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5，0.012 5；

优化值（Tx）：0.1，0.05，0.05，0.09，0.1，0.1，0.1，0.01，0.04；

经过上述计算和修正后，将优化值代入Zemax，进行1 000次蒙特卡罗模拟，得到透镜厚度公差和透镜位置公差对应目标函数公差分别为0.335 3和0.134 5。与此类似，依次对折射率公差，光圈公差和透镜偏心公差进行公差分配，并将优化后的公差值代入Zemax 进行公差计算，得到目标函数值分别为0.604 6和0.302 5，符合设计要求。

4 结 论

针对可见光变倍光学系统，提出了一种基于传递函数灵敏度的公差分析方法和分析流程，结果表明，在保证成像质量的前提下，通过这个方法可以放宽对公差的要求，降低加工和装调难度，该方法也适用于其他光机系统。

［1］ 王海涛，耿安兵，杨长城.切换变倍光学系统设计［J］.光学学报，2010，30（3）：872－875.

［2］ 王黎明，杨华民，李共德.用传递函数法优化光学公差［J］.光学技术，1998（1）：84－88.

［3］ 章慧贤.光学传递函数的发展及其应用［J］.光学仪器，1996，18（4）：28－31.

［4］ CHANG C W.Tolerance analysis of lenses with high zoom ratio［J］.SPIE，2006，6034：60341.

［5］ SMITH W J.Modern optical engineering［M］.3rd ed.New York：McGraw－Hill，2000.

［6］ 王之江.实用光学技术手册［M］.北京：机械工业出版社，2006.