频谱校正方法在激光测速中的研究＊

潘瑞雪，梁 平，孟祥昊

（安徽工业大学 电气信息学院，安徽 马鞍山 243002）

引 言

在激光多普勒测速技术［1］中，多普勒信号处理方法十分关键，目前多普勒信号处理最常见的方法是对采集的信号进行快速傅里叶变换（fast fourier transform，FFT）。然而经过长期的实践和理论分析表明：经FFT 得到的离散频谱，其频率、幅值和相位存在精度低的问题。而实测多普勒信号本身又具有信号弱、噪声干扰大的特点，影响FFT 结果。由此可见，直接将FFT 结果的谱峰值对应的频率作为多普勒频移已经不能满足激光测速的精度需求。因此，必须考虑采用离散频谱校正的方法对FFT 的结果进行校正，以达到提高激光测速精度的目的。为此，详述了三种校正方法的基本原理，并对理想正弦信号、不同信噪比的加噪正弦信号和实测多普勒信号进行频谱校正仿真研究。

1 离散频谱校正的方法

以最简单的激光多普勒信号（正弦信号）为例，其频率为10kHz，设采样频率为100kHz，采集128点，对采得的序列做FFT，其FFT 结果如图1所示，其峰值谱线号k为14，对应的频率为10.156 25kHz，与分析信号的频率10kHz存在较大误差，因此要对峰值谱线号进行校正，以精确求取分析信号的频率。设归一化的频率校正量为Δf1，则校正后的频率为：

式中，fs为采样频率，N 为采样点数。

1.1 比值校正法的基本原理

比值校正法是利用频率归一化后的差值为1的主瓣峰顶附近的两条谱线的窗谱函数的比值，建立一个以校正频率为变量的方程，解出方程以对频率进行校正。加Hanning窗［2］时的归一化频率校正量为：

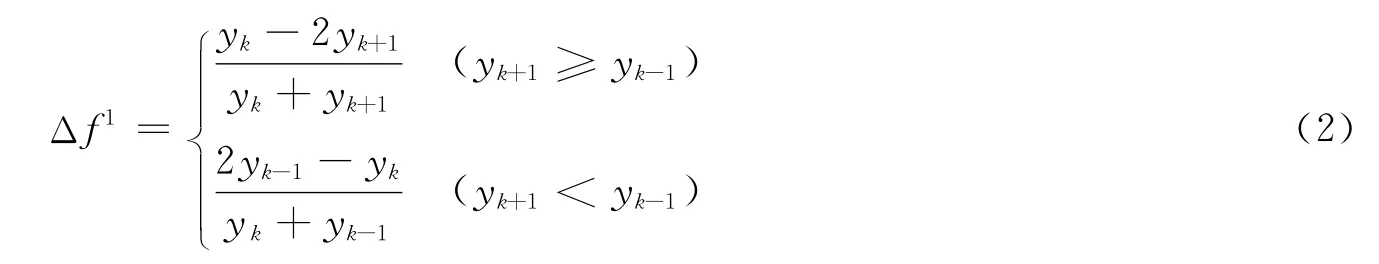
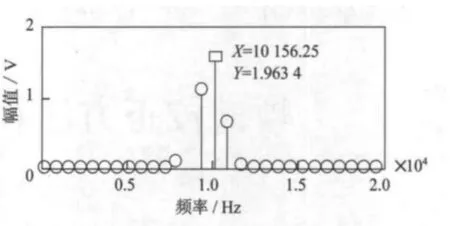
图1 FFT 结果图Fig.1 Fast Fourier transform with 128point

式中，k为幅值谱最大值谱线号，yk为幅值谱第k 条谱线幅值。

1.2 能量重心校正法的基本原理

能量重心校正法是基于各种窗函数的离散频谱的能量重心无穷逼近主瓣中心的特点，通过利用主瓣内功率谱值较大的几条谱线来精确求出主瓣的中心坐标。同样以Hanning［3］窗为例，根据Hanning窗的能量重心特性有：

化简式（3），求得主瓣中心为：

设归一化频率的校正量为Δf1，由式（4）知：

1.3 相位差校正法的基本原理

相位差校正法是对原始分析信号进行两次采集，对采得的两段信号分别做傅里叶变换，然后根据对应峰值谱线的两个相位的相位差求得谱峰处的准确频率。针对多普勒信号，采取这样的方法来获得这两段信号：对分析信号采集N 点，得到第一段时间序列；平移第一段信号的前N／2个点，平移N／4点后将前后N／4点置零，构造出第二段时间序列［4］。对两段序列分别加相同的窗函数进行N 点的FFT 变换，假设变换后其各自对应的峰值谱线号均为k，则频率校正量的校正公式为：

式中，θk1和θk2分别为k点处对应的相位。

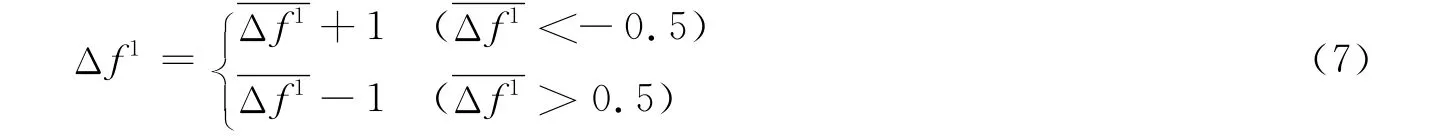
在实际研究中发现，由于噪声干扰等因素的影响，两段样本的峰值谱线号可能并不相同，分别为k1和k2，此时直接使用式（6）进行计算常不能得到正确结果，针对这种情况需做如下处理：假设k1＜k2，校正后应满足k1≤（k－Δf1）≤k2，则若令k＝k1，Δf1＞0 时，Δf1＝－Δf1；Δf1＜0 时无需修正；若令k＝k2，Δf1＜0时，Δf1＝－Δf1；Δf1＞0时无需修正［5］。

2 三种离散频谱校正方法的仿真研究

2.1 三种方法对不同频率理想正弦信号的仿真研究

基于激光多普勒信号的特征，使用以上三种校正方法对频率分别为100kHz和700kHz的理想正弦信号进行频谱校正仿真计算［6］，其中采样频率为理想正弦信号频率的10倍，采样点数为512点，所加窗函数为Hanning窗。其仿真结果如图2～图4所示。

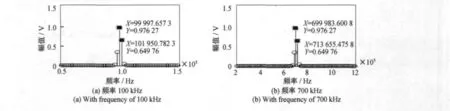
图2 不同频率的理想正弦信号其频谱经比值法校正的结果Fig.2 Results of ratio method for sine signal with different frequency

图3 不同频率的理想正弦信号其频谱经能量重心法校正的结果Fig.3 Results of energy centrobaric method for sine signal with different frequency

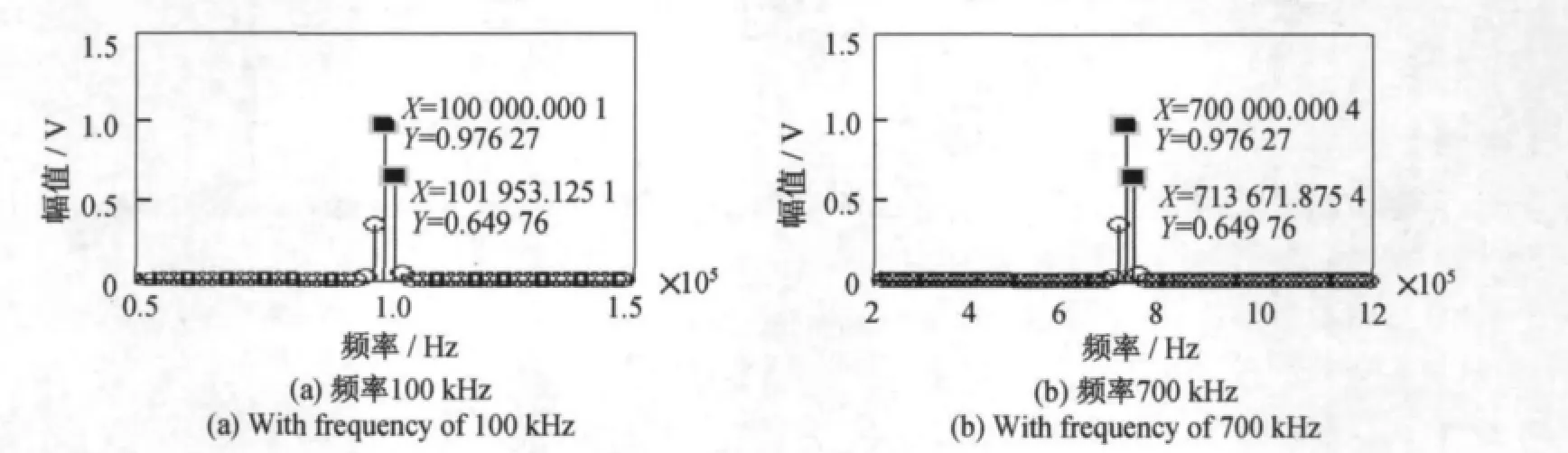
图4 不同频率的理想正弦信号其频谱经相位差法校正的结果Fig.4 Results of phase difference method for sine signal with different frequency

表1 加Hanning窗无噪声时三种方法的校正结果Tab.1 Results of three methods for sine signal with no noise adding Hanning window Hz

表1是加Hanning窗无噪声时的三种方法校正前后对比结果，分析仿真数据可知，未经校正的频率相对于理论频率误差较大，而在理想情况下，三种方法的频率校正精度都很高。

2.2 三种方法对不同信噪比的加噪正弦信号的仿真研究

在高斯白噪声背景下，使用三种校正方法对信噪比（signal to noise ratio，SNR）分别为－2.33dB、0dB和6dB的频率为700kHz的加噪正弦信号进行频谱校正仿真实验［7］，其中采样频率为7 MHz，采512点，加Hanning窗。仿真结果如图5～图7所示。

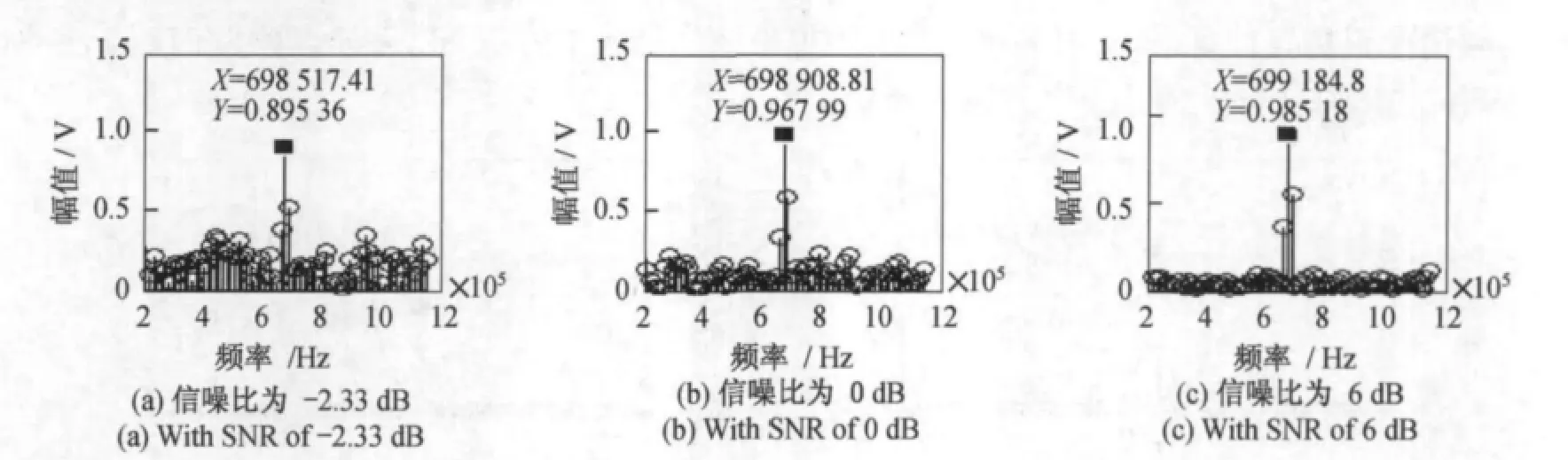
图5 不同SNR 的加噪正弦信号，其频谱经比值法校正的结果Fig.5 Results of ratio method for sine signal with noise and different SNR

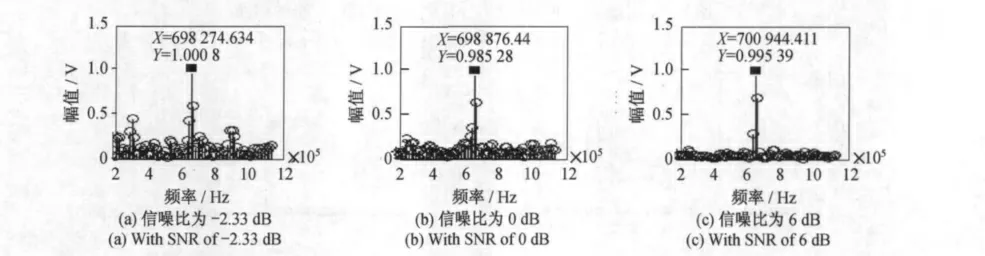
图6 不同SNR 的加噪正弦信号，其频谱经能量重心法校正的结果Fig.6 Results of energy centrobaric method for sine signal with noise and different SNR

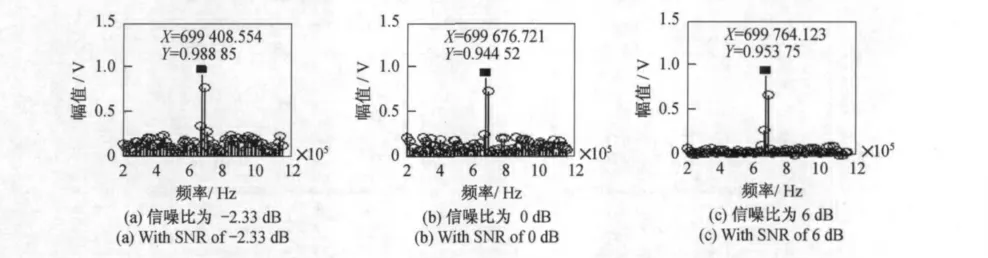
图7 不同SNR 的加噪正弦信号，其频谱经相位差法校正的结果Fig.7 Results of phase difference method for sine signal with noise and different SNR

表2 加Hanning窗不同信噪比时三种方法的校正结果Tab.2 Results of three methods for sine signal with different SNR adding Hanning window

表2为加Hanning窗有噪声时的频率校正结果，分析表2可以得出，在不同信噪比的情况下，三种校正方法依然可以保持较高的校正精度，校正精度随信噪比的增大而提高。虽然相位差法的校正效果更为理想，但其算法本身存在将相位差调整到主值区间而导致校正错误的情况，且相对于其他两种算法复杂度稍大；而比值法在含噪声情况下可能导致插值方向错误；考虑到能量重心法算法简单，处理速度快，虽然校正精度没有其他两种算法理想，但其抗噪性能稳定，而且通过加窗可显著提高其校正精度［8］，因此，选用能量重心法作为多普勒信号处理的频率校正算法，用于实测研究。

3 能量重心法的应用

以直流电机带动的转盘上某待测点的线速度作为测量对象，对运动物体测量三次，得到三组实测多普勒信号，见图8（a）～图8（c），对应的采样频率分别为30kHz、2MHz和10MHz，采样点数N＝2 048。将所测线速度对应的多普勒频率作为频率标准，采样能量重心法对频率进行校正，对比分析校正前后的频率值［9］。图9为三组实测信号经能量重心法校正后的结果。

表3为采用能量重心法时，三组实测的多普勒信号频率校正前后的对比结果，由校正结果可以得出，校正后的频率更加接近真实频率，校正效果明显。因此，在激光多普勒信号处理器中使用频率校正技术是切实可行的。

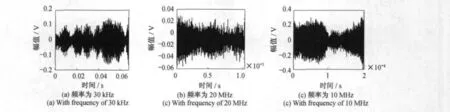
图8 三组不同频率的实测多普勒信号Fig.8 Three groups of measuring Doppler signal with different frequency

图9 不同频率的实测信号经能量重心法校正后的结果Fig.9 Results of energy centrobaric method for measuring Doppler signal with different frequency

表3 三组实测多普勒信号的校正结果Tab.3 Results of energy centrobaric method for measuring Doppler signal

4 结 论

通过理论分析、仿真实验和实际应用，结果表明，三种方法均有很高的校正精度。在三种算法中，相位差法需进行两次采样和FFT 运算，虽校正精度较高，但运算复杂；比值法算法简单，且校正精度较高，但受到噪声的影响，可能导致插值方向错误，以致校正效果不佳；能量重心法是一种近似算法，虽校正精度没有其他两种算法高，但其算法简单，抗噪性能稳定，而且通过加窗函数，相对弥补了精度低的缺点。因此，综合考虑了各算法的复杂度和抗噪性能等因素，本文选择了能量重心法对实测多普勒信号进行了频率校正，校正效果理想。研究结果表明，使用能量重心法对激光多普勒信号进行频谱校正处理是实用而有效的。

［1］ 王兰美，张凯华，马瑞亭.基于双光束－双散射的激光多普勒水流速测量［J］.光学仪器，2009，31（3）：5－7

［2］ 徐传燕，丁 康，林慧斌，等.离散频谱分析比值校正法幅值和相位的抗噪性分析［J］.振动工程学报，2011，24（6）：637－638.

［3］ 林慧斌.离散频谱校正理论的控制性能研究及其在工程中的应用［D］.广东：华南理工大学，2010：24－26.

［4］ 黄云志，徐科军.基于相位差的频谱校正方法的研究［J］.振动与冲击，2005，24（2）：77－79.

［5］ 刘文昌，韩静娜，刘 杰，等.激光多普勒测速中的频谱校正及其应用［J］.中国激光，2003，30（7）：644－646.

［6］ 周 健，龙兴武，魏 国.基于Labview 的激光多普勒测试仪的频谱校正［J］.强激光与粒子束，2010，22（1）：9－11.

［7］ 丁 康，郑春桥，杨志坚.离散频谱能量重心法频率校正精度分析及改进［J］.机械工程学报，2010，46（5）：44－46.

［8］ 曹 翌，丁 康，杨志坚.离散频谱校正方法的抗噪性能研究［J］.制造业自动化，2011，33（7）：41－42.

［9］ 周 健，黄 华.频谱细化及频谱校正技术在激光多普勒测试仪中的应用［J］.激光与红外，2010，40（2）：148－149.