2－qubit系统的纠缠鲁棒性

史淑惠，许龙飞

（1.邯郸学院 物理与电气工程系，河北 邯郸 056005；2.河北大学 物理科学与技术学院，河北 保定 071002）

量子纠缠是一个最微妙和迷人的自然现象，在量子计算和量子信息中起着非常重要的作用［1］.量子纠缠作为量子信息过程的重要资源，可以应用到许多方面如：量子隐形传态［2］、量子计算［3］、量子编码［4］、量子密码［5］等等.然而，对于一个量子系统而言，它必然在处于某种环境中并与环境发生相互作用，通常会导致系统纠缠的降低.在量子信息处理上，这种退相干使得系统出现不稳定的现象.因此，研究量子纠缠的动力学特性尤为重要.最近有许多相关的工作被报道，例如，一个处于纠缠的量子态在环境的影响下其纠缠度会在有限的时间内变为零，这种现象被称为纠缠猝死（entanglement sudden death，ESD）［6］，并且这一现象已经在2－quibt光学系统中被观测到［7］.量子纠缠在环境噪声的影响下是非常脆弱易被破坏的，因此纠缠态对噪声的抵抗能力在量子信息过程中是一个很重要的问题.纠缠的鲁棒性便是反映该能力的一个量.1999年，Vidal和Tarrach［8］将一个纠缠态与可分离态混合时当纠缠恰好消失时可分离态混入的比例称为该态的鲁棒性.2002年，Simon和Kempe［9］考虑了将处于纠缠态的qubit置于相互独立的环境中的情况，以完全退纠缠时噪声的大小作为纠缠态的鲁棒性.2010年，Zhao和Deng［10］给出了2－qubit纯态在退极化噪声下鲁棒性与纠缠度的简单关系.本文基于量子纠缠这一热门领域，通过分析在退极化噪声下纠缠态随时间的演化特性，并给出一类2－qubit态的纠缠抗噪声能力——纠缠鲁棒性解析关系.

1 模型

对于开放系统而言，退相干是一种常见的量子现象.在研究的问题中，考虑一个初始时刻具有纠缠的2－qubit系统在退极化噪声下的演化特性，此外单qubit能够与环境独立地发生相互作用.假设所有qubit受到相同的退极化过程，通过主方程的方法可以得到单qubit的动力学演化形式.系统与环境发生相互作用，在海森堡绘景下，系统的演化过程可以用Liouville方程表示出来，利用量子力学中的Born近似，将系统的演化内核部分保留到二阶项.同时忽略环境的记忆效应（取Markovian近似），于是得到Lindblad形式的主方程.将其表示为Kraus算符的形式［11］

2 纠缠度

3 2－qubit纠缠猝死现象

在退极化噪声下，为了不失一般性，从两方面考虑2－qubit系统：纯态和混态.

对于纯态而言，它是最简单的两体系统.一般的2－qubit纯态可以表示为｜ψ〉＝a｜00〉＋b｜01〉＋c｜10〉＋d｜11〉（其中｜a｜2＋｜b｜2＋｜c｜2＋｜d｜2＝1），在局域幺正操作下，任意2－qubit纯态等价于｜ψ〉＝cosθ｜00〉＋sinθ｜11〉（θ∈［0，π／2］），这是纯态的Schmidt分解形式［1］.在退极化噪声的作用下，2－qubit纯态的纠缠 Concurrence变为

图1 纯态的纠缠随参数的演化Fig.1 Plot of the evolution of Concurrence with parameters for pure state

图2 Werner态的纠缠随参数演化Fig.2 Plot of the evolution of Concurrence with parameters for Werner state

因此不难看出，在2－qubit系统中，无论是纯态还是混态都出现了纠缠猝死现象，但是这2种态的纠缠猝死特性并不一致.对于纯态系统而言，系统本身比较简单，在退极化噪声下呈线性改变；而在混态系统中状态参量逐渐增多，在噪声作用下多参数混态系统的演化状态往往不再是单调的变化，状态将变得更加复杂.

下面介绍一个物理量——纠缠鲁棒性，用它来分析解决在相同环境下，量子系统对噪声的抵抗能力将会如何，并且以此来区分该能力的强弱.

4 纠缠鲁棒性

首先，不同于文献［8－10］中对纠缠鲁棒性的定义，定义纠缠鲁棒性为［16］

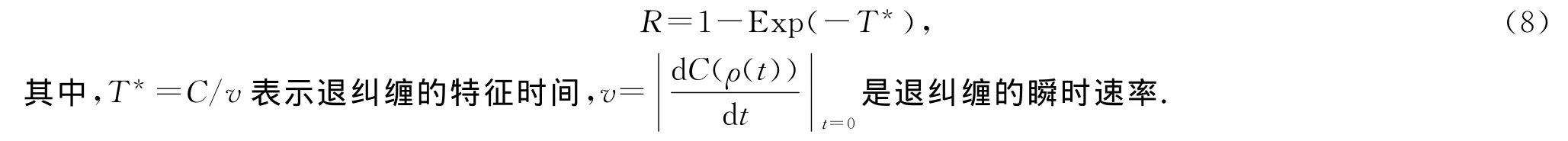
在退极化噪声下，用数值模拟的方法给出了纠缠和纠缠鲁棒性的关系（如图3）.从图3中，明显可以看到纠缠鲁棒性存在边界，那么边界态对应形式是什么呢？

因为2－qubit纯态是2－qubit态中最简单的状态，故首先考虑这一形式.对于任意2－qubit纯态｜ψ〉＝cosθ｜00〉＋sinθ｜11〉（θ∈［0，π／2］），利用p＝1－exp［－κt］（由于κ表示衰减常数且在相同环境下比较系统稳定性方面是一致的，因此可取κ＝1），可以得到退纠缠速率

结果与文献［10］很相似，其纠缠鲁棒性仅仅取决于纠缠度C.另外，可以看到纯态的纠缠和鲁棒性的关系正好对应图3中的边界，图中用黑粗实线标出.

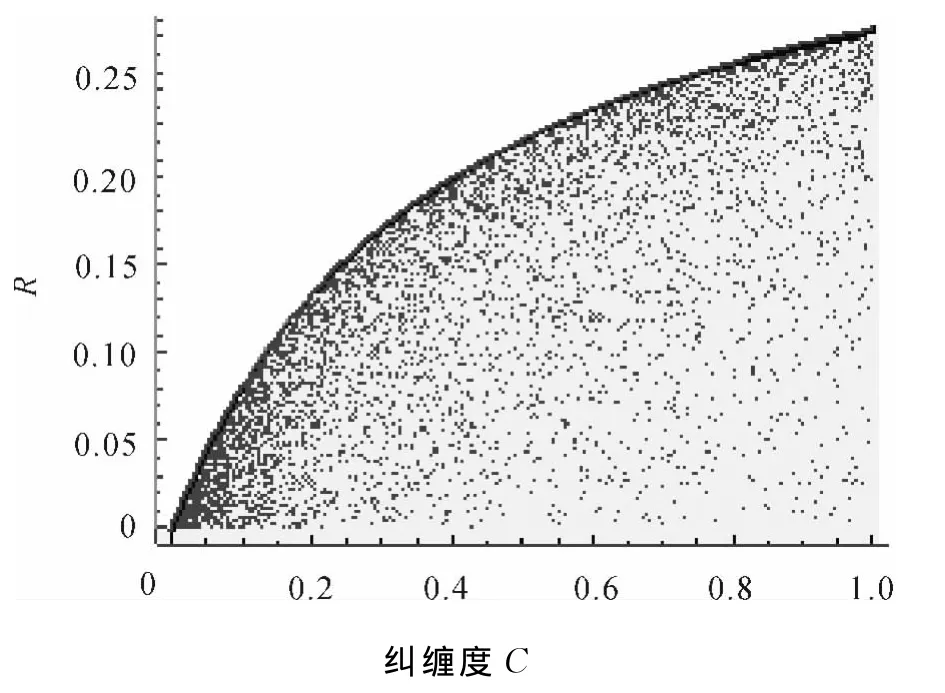
图3 10 000个任意2－qubit态的纠缠鲁棒性R与纠缠（Concurrence）的关系Fig.3 Plots of the relations between the entanglement robustness and Concurrence of randomly generated two－qubit states 10 000randomly generated states and the curve showing the upper bound

图4 Negativity对纠缠鲁棒性R的影响（等高线表示Negativity的值）Fig.4 Plot of the effect of Negativity on the entanglement robustness，with the contours of the Negativity

为了进一步分析问题，考虑一类态ansatz态［17］

其中0≤x，y，a，b，γ≤1且x＋y＋a＋b＋γ＝1，可以看到 Werner态也满足ansatz态的形式.该态的纠缠度Concurrence为

对于这类态而言，发现在退极化噪声作用下态的形式不发生改变，只是参数会相应改变.在退极化噪声作用下，可以看到所研究的态ρansatz变为ρ（t），即

从式（16）可以看到ansatz态的纠缠鲁棒性仅仅取决于3个参量γ，a，b，即一旦这3个参量给定，那么纠缠鲁棒性就被确定下来了.

当a＝b且a，b≠1时，该态的鲁棒性为R＝1－Exp［－C／（2C＋1）］，这与纯态的结果一致，满足任意2－qubit态的上边界关系（见图3）.另外，还可以看到，在退极化噪声作用下，当初态为纯态时，系统演化过程中纠缠鲁棒性始终保持R－C（其中R＝1－Exp［－C／（2C＋1）］）这一关系.如果初态为Bell态（即最大纠缠态C＝1），那么该态在退极化噪声下逐步演化将会沿着边界线（图3中的实线）进行变化，从最大纠缠态逐渐变为无纠缠态；纠缠鲁棒性也会相应减小甚至变成0，即抗噪声能力逐渐降低.对于其他满足a＝b纠缠态（可看出Werner态只是属于这类态中的一种形式）的演化情况同纯态的情况相似，只是起始纠缠大小不同而已.对于一般ansatz态（a≠b且a，b不同时为0）来说，也有相似结论，只是演化曲线Ra－Ca不再是边界线.

通过以上分析，可以看到对于该类对角混态（ansatz态），在每一时刻纠缠的鲁棒性（即抗噪声能力）都可以被确定，即任意时刻ansatz态的纠缠鲁棒性都是确定的.另外，根据纠缠和鲁棒性的关系，可看出纠缠猝死时间在很大程度上取决于初始纠缠大小和纠缠鲁棒性，而且纠缠鲁棒性越大纠缠猝死时间越长.

下面分析其他纠缠度量对纠缠鲁棒性的影响，如Negativity［18］.任意2－qubit纠缠可以表示为N＝的负本征值，T表示对ρ的子系统A的部分转置.对于ansatz态来说，为AAB了方便，取x＝y＝0，此时态记为ρn.为了更加清晰地呈现问题，将Negativity作为等高线来刻画另一纠缠度对纠缠鲁棒性的影响（如图4）.从图4中，可以看到，当Concurrence一定时，Negativity越大纠缠鲁棒性越强，那么纠缠猝死的时间将会更长.由于2－qubit系统的纠缠的度量方式是多样化的，所以对于其他纠缠度的影响在此就不再一一赘述.

5 结论

分析了2－qubit量子系统在退极化噪声作用下的一些纠缠特性.通过分析对角混态的纠缠鲁棒性（系统抵抗噪声的能力），给出了这类量子态的解析关系.由于两比特系统在具有各向同性噪声（退极化噪声）下，对角混态（ansatz）可以通过不改变本身纠缠的局域幺正操作得到绝大多数的两比特态，因此说系统纠缠猝死时间对纠缠和纠缠鲁棒性有一定的依赖性.纠缠作为量子通讯和量子计算的信息载体，其稳定性是至关重要的，选择具有较强抗噪能力的量子态是很必要的，期望对系统纠缠鲁棒性的分析可以为量子态调控方面起到一定的促进作用.

［1］NIELSEN M A，CHUANG I L.量子计算和量子信息［M］.郑大钟，赵千川，译.北京：清华大学出版社，2005.

［2］BENNETT C，BRASSARD G，CREPEAU C，et al.Teleporting an unknown quantum state via dual classical and Ein

stein－Podolsky－Rosen channels［J］.Phys Rev Lett，1993，70：1895－1899.

［3］GROVER L K.Quantum mechanics helps in searching for a needle in a haystack［J］.Phys Rev Lett，1997，79：325－328.［4］BENNETT C H，WIESNER S J.Communication via one－and two－particle operators on Einstein －Podolsky －Rosen states［J］.Phys Rev Lett，1992，69：2881－2884.

［5］EKERT A K.Quantum cryptography based on Bell's theorem ［J］.Phys Rev Lett，1991，67：661－663.

［6］YU T，EBERLY J H.Finite－time disentanglement via spontaneous emission［J］.Phys Rev Lett，2004，93：140404.［7］ALMEIDA M P，MELO F D，HOR－MEYLL M，et al.Environment－induced sudden death of entanglement［J］.Science，2007，316，579－582.

［8］VIDAL G，TARRACH R.Robustness of entanglement［J］.Phys Rev A，1999，59：141－155.

［9］SIMON C，KEMPE J.Robustness of multiparty entanglement［J］.Phys Rev A，2002 65：052327（1－4）.

［10］ZHAO Baokui，DENG Fuguo.Residual effect on the robustness of multiqubit entanglement［J］.Phys Rev A，2010，82：014301（1－4）.

［11］BORRAS A，MAJTEY A，PLASTINO A，et al.Robustness of highly entangled multiqubit states under decoherence［J］.Phys Rev A，2009，79：022108.

［12］DüR W，BRIEGEL H.Stability of macroscopic entanglement under decoherence［J］.Physical review letters，2004，92：180403.

［13］HILL S，WOOTTERS W.Entanglement of a pair of quantum bits［J］.Phys Rev Lett，1997，78：5022－5025.

［14］WOOTTERS W.Entanglement of formation of an arbitrary state of two qubits［J］.Phys Rev Lett，1998，80：2245－2248.

［15］WERNER R F.Quantum states with Einstein－Podolsky－Rosen correlations admitting a hidden－variable model［J］.Phys Rev A，1989，40：4277－4281.

［16］ZHANG Fulin，JIANG Yue，LIANG Mailin，et al.Speed of disentanglement in multiqubit systems under depolarizing channel［J］.Annals of Physics，2013，333：136－154.

［17］MUNRO W，JAMES D F V，WHITE A G，et al.Maximizing the entanglement of two mixed qubits［J］.Phys Rev A，2001，64：030302（R）.

［18］YCZKOWSKI K，HORODECKI P，SANPERA A，et al.Volume of the set of separable states［J］.Phys Rev A，1998，58：883－892.