基于锚固站的UT1-UTC预报误差抑制技术❋

孟繁智，王成余，刘文祥，欧 钢

（1.国防科技大学电子科学与工程学院，长沙 410073；2.解放军95899部队，北京 100085；3.扬州环境资源职业技术学院测绘工程教研室，江苏扬州225127）

基于锚固站的UT1-UTC预报误差抑制技术❋

孟繁智1，2，❋❋，王成余3，刘文祥1，欧 钢1

（1.国防科技大学电子科学与工程学院，长沙 410073；2.解放军95899部队，北京 100085；3.扬州环境资源职业技术学院测绘工程教研室，江苏扬州225127）

针对导航星座自主定轨中的UT1－UTC预报误差，分析了其对星座定轨的影响，并对预报精度进行了仿真；给出了基于锚固站的定轨算法，并使用Walker12/3/1星座进行了仿真。结果表明：UT1－UTC预报误差对星座定轨精度影响较大，107ms的预报误差将引入168m的星座位置误差；引入锚固站后，这一影响被有效抑制，抑制效果随锚固站测量精度的提高而增强。

导航星座；协调世界时；锚固站；自主定轨；预报误差

1 引言

目前，已经建成或正在建设的卫星导航系统，如美国的GPS系统、俄罗斯的GLONASS系统、欧盟的Galileo系统、中国的“北斗”系统等，作为重大的军事信息系统，这些导航系统无一例外地考虑了导航战的需求。基于星间观测完成星座的自主定轨是满足导航战需求的一项重要技术，该技术在卫星之间建立星间观测链路，当卫星失去与地面控制系统的联系后，通过对星间观测数据的处理保证卫星在一定时间段内自主工作，提高整个导航系统的生存能力。

在应用星间链路进行自主定轨的过程中，由于卫星运动方程的建立以及卫星轨道的解算都是在地心惯性系（ECI）中进行的，而导航星座需要向用户广播的却是卫星在地固坐标系（ECEF）中的星历，因此在导航星座的自主定轨中，需要进行坐标系ECI和ECEF之间的转换。在自主定轨模式下，导航星座无法获得精确的地球定向参数，只能使用预报模型提供的预报结果，故地球定向参数不可避免地存在误差，该误差会随着坐标系转换导致卫星在ECEF中的轨道发生偏差，最终影响用户的定位精度。

地球定向参数包括世界时与协调世界时之差（即UT1－UTC）和极移两个参数，UT1－UTC反映地球自转角速度的变化，而极移反映地球瞬时极相对平均极的移动。研究表明［1－3］，极移参数可以精确预报，对导航星座的影响可以忽略，而UT1－UTC预报精度有限，对导航星座的影响较大。

本文首先给出UT1－UTC预报误差对卫星轨道的影响，然后给出了基于锚固站的误差抑制技术的实现流程，最后通过仿真算例评估该技术对UT1－UTC预报误差的抑制性能。

2 UT1-UTC预报误差对卫星轨道的影响

在ECI向ECEF转换的过程中，涉及岁差矩阵P、章动矩阵N、地球自转矩阵B2和地球极移矩阵B1等4个转换矩阵［4］，对于ECI坐标系中的位置坐标r＝（x，y，z）T，转换到ECEF中的坐标rb＝（xb，yb，zb）T为

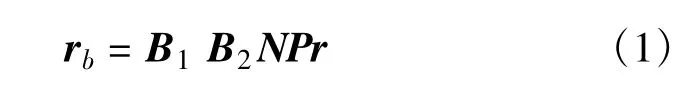
UT1-UTC预报误差的影响体现在地球自转矩阵B2中，B2完成瞬时真赤道坐标系向准地固系的转换，表达式为［4］

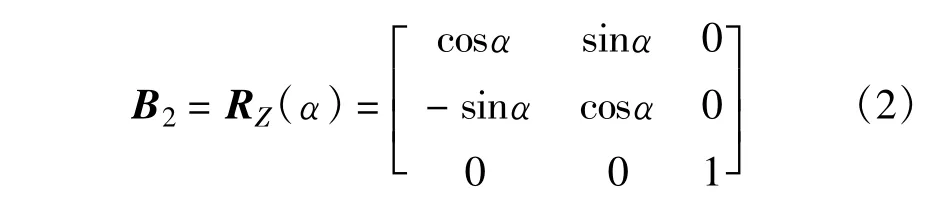
其中，α为格林尼治真恒星时时角。

假设UT1-UTC的预报误差为δT，根据α与UT1-UTC的关系［4］，α将引入误差

其中，˙Ωe＝7.292 115×10－5rad/s为地球自转角速度。

格林尼治真恒星时时角引入误差后，将导致ECEF中的坐标出现偏差，偏差矢量为

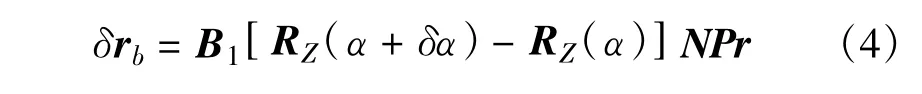
参考矩阵和向量范数的相关理论，矢量长度δrb＝‖δrb‖2，其中‖·‖2为2范数，并且根据2范数的相容性可知：

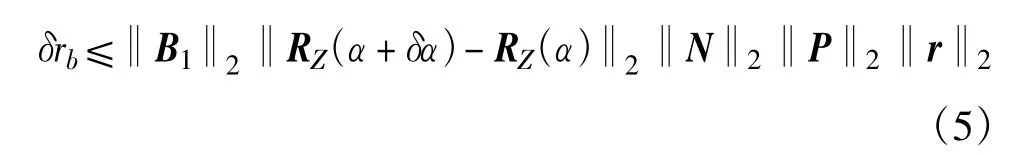
由于B1、N和P均是正交矩阵，故‖B1‖2＝‖N‖2＝‖P‖2＝1。根据式（2）容易计算得到‖RZ（α＋δα）－RZ（α）‖2＝2sin（δα/2），于是式（5）简化为

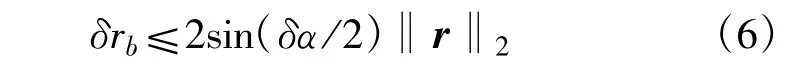
考虑到δα≪1，并且对于圆轨道或近圆轨道卫星，偏心率e≈0［4］，于是有‖r‖2≈a（a为轨道半长轴），因此ECEF中的坐标偏差可近似为

在星座轨道根数已知的条件下，通过式（7）即可对UT1-UTC预报误差的最大影响作出评估。

3 基于锚固站的误差抑制技术

根据UTC的定义，UTC与UT1的偏差在0.9 s之内，如此大的偏差如果不加处理的话，将引入较大的轨道误差。为了尽可能减小UT1-UTC偏差对轨道的影响，已有的方法主要集中在优化UT1-UTC的预报模型上，即基于过去若干年的UT1-UTC数据进行数学拟合，然后根据拟合结果对UT1-UTC进行预报。从1978年Meyerhoff提出傅里叶级数预报模型［5］开始，众多学者提出了多种改进模型［6］，但遗憾的是，尚未发现一种模型可以在任何预报区间内提供最优的精度，有关工作尚在研究之中。

目前已有不少论文对导航卫星的自主定轨进行了研究，但涉及地球定向参数长期预报误差修正问题的研究较少，武汉大学的李征航从坐标转换公式出发提出了地面修正方法［3］，该方法不改变导航星座播发的卫星星历，而是通过地面用户修正的方法校正地球定向参数的长期预报误差。本文的出发点是在传统的自主定轨算法基础上，通过较少量的修改，即可实现基于锚固站的星历修正，地面用户可直接接收使用而不需要进行修正。

锚固站是指位于地面精确标定位置的接收机，该接收机接收所有可见卫星的下行信号，计算伪距和钟差，然后将处理结果注入到卫星。Rawicz等学者提出在卫星定轨中使用锚固站的思路并于1996年申请了专利［7］，Rajan等学者将锚固站引入到导航星座的自主定轨中，解决了星间观测秩亏导致的星座整体旋转问题［8］。使用锚固站抑制UT1－UTC预报误差的基本原理是由于锚固站与地球一同旋转，星上处理器在融合星间与星地测量信息时，锚固站的位置基准信息即被引入到导航星座的定轨中，这一原理类似航海中的船锚，故而得名。下面给出算法处理流程。

（1）观测模型

假设在某时刻t，导航星座获得观测Y（m×1维），则观测方程可以表示为Y＝G（X，t）＋Δ，其中，G（X，t）是观测真值，X是星座在t时刻的状态矢量（6N×1维），Δ是观测噪声矢量（m×1维），N为卫星总数，每颗卫星包含6个状态变量（三维位置和三维速度）。

观测方程线性化后的模型［9］为

其中，y是观测残差矢量（m×1维），H是观测矩阵（m×6N维），x是待估计的改正数矢量（6N×1维）。

（2）星间观测矩阵

假设第u个观测量对应的是卫星i对卫星j的距离观测，则矩阵H的第u行可以表示为

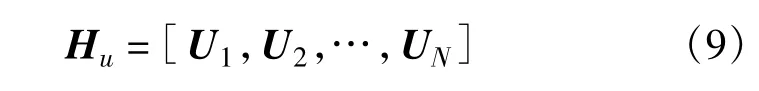
其中：

式中，ti是卫星i的观测时刻，tj是卫星j的信号发射时刻，Gu是星间测距值，t0是星座定轨时刻，ri（t）和rj（t）分别是卫星i和卫星j在t时刻的位置矢量（3×1维），Φi和Φj分别是卫星i和卫星j的状态转移矩阵（6×6维）。

（3）星地观测矩阵

假设第v个观测量对应的是锚固站对卫星j的距离观测，则矩阵H的第v行可以表示为

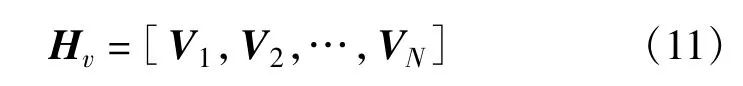
其中，锚固站坐标是已知量，在联合定轨中不对其进行估计，于是有

式中，rG（t）是锚固站在t时刻的位置矢量，Gv是星地测距值。

星上处理器使用扩展卡尔曼滤波器，联合星间与星地测量数据进行滤波处理，从tk－1时刻到tk时刻的滤波过程为

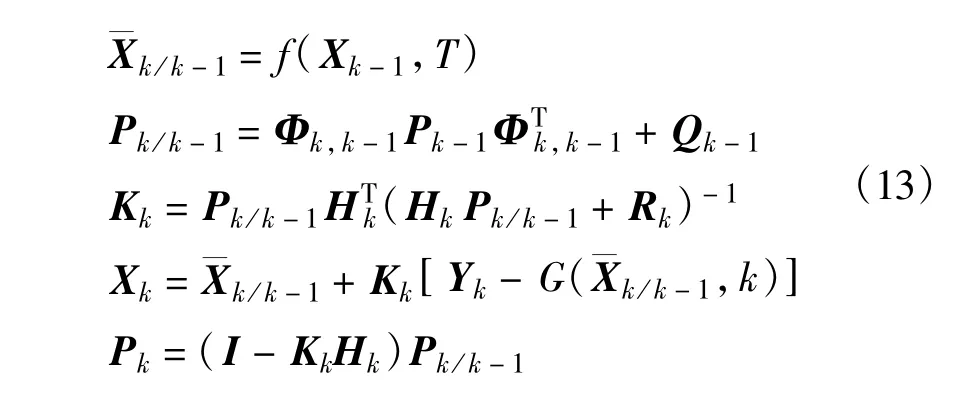
式中，T＝tk－tk－1为滤波周期，f（·）为卫星动力学方程，Rk是由星间观测噪声方差和星地观测噪声方差构成的对角矩阵，Yk为星间观测值和星地观测值构成的观测矢量。

联合星间与星地观测的定轨处理流程如图1所示。锚固站布设在位置已知点上，对导航星座进行观测，然后将自身位置坐标和测距值等信息上行注入给卫星。星上处理器首先将锚固站坐标转换到ECI中，然后根据轨道初值和摄动力模型计算扩展卡尔曼滤波器所需的参考轨道，使用锚固站提供的星地观测数据和卫星之间的星间观测数据，更新卡尔曼滤波器，完成定轨处理，最后将轨道坐标转换到ECEF中。图1中，REF2J表示ECEF到ECI的坐标系转换矩阵，RJ2EF表示ECI到ECEF的坐标系转换矩阵，两者均含有UT1-UTC预报误差的影响。

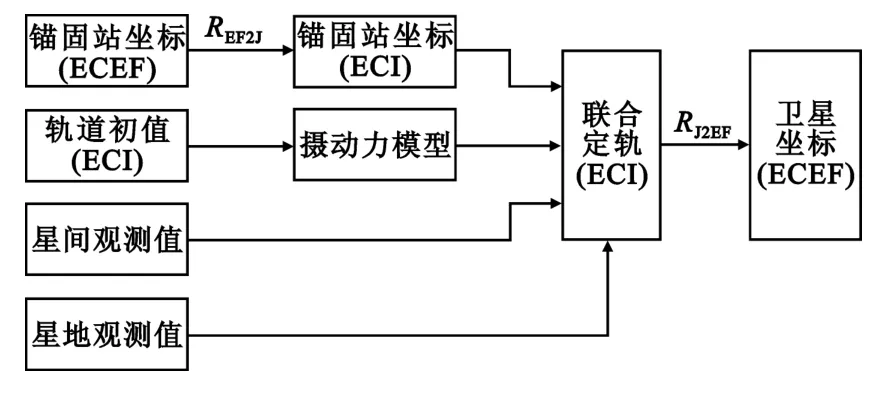
图1 联合定轨的处理流程Fig.1 The processing flow of combined orbit determination

4 仿真计算与结果分析

4.1 导航星座仿真参数

目前世界上主要的卫星导航系统，如美国的GPS系统、俄罗斯的GLONASS系统、欧盟的Galileo系统、中国的下一代“北斗”系统，均主要应用近圆轨道的MEO卫星进行星座布局，不失一般性，选择MEO卫星进行仿真分析。由于本文主要研究锚固站对UT1-UTC预报误差的抑制能力，星座布局不影响分析结论，因此选择相对简单的Walker星座，以简化仿真条件。

假设导航星座由12颗MEO组成，按Walker12/3/1分布，轨道高度为20 000 km，轨道倾角为55°，近地点角距为0°。各卫星编号为W ij，i对应轨道面序号（取值1，2，3），j对应轨道面上的卫星序号（取值1，2，3，4），根据Walker星座的特点，每个轨道面上的4颗卫星均匀分布，3个轨道面的升交点赤经依次为0°、120°、240°，相邻轨道面的卫星相差为30°。星间测距模式参考GPS Block II-R卫星［10］，即使用TDMA模式发射测距信号，每颗卫星发射信号时隙为1.5 s，在每个时隙内，只允许一颗卫星发射信号，其他所有卫星处于接收状态，星间测距信号发射时隙见表1。

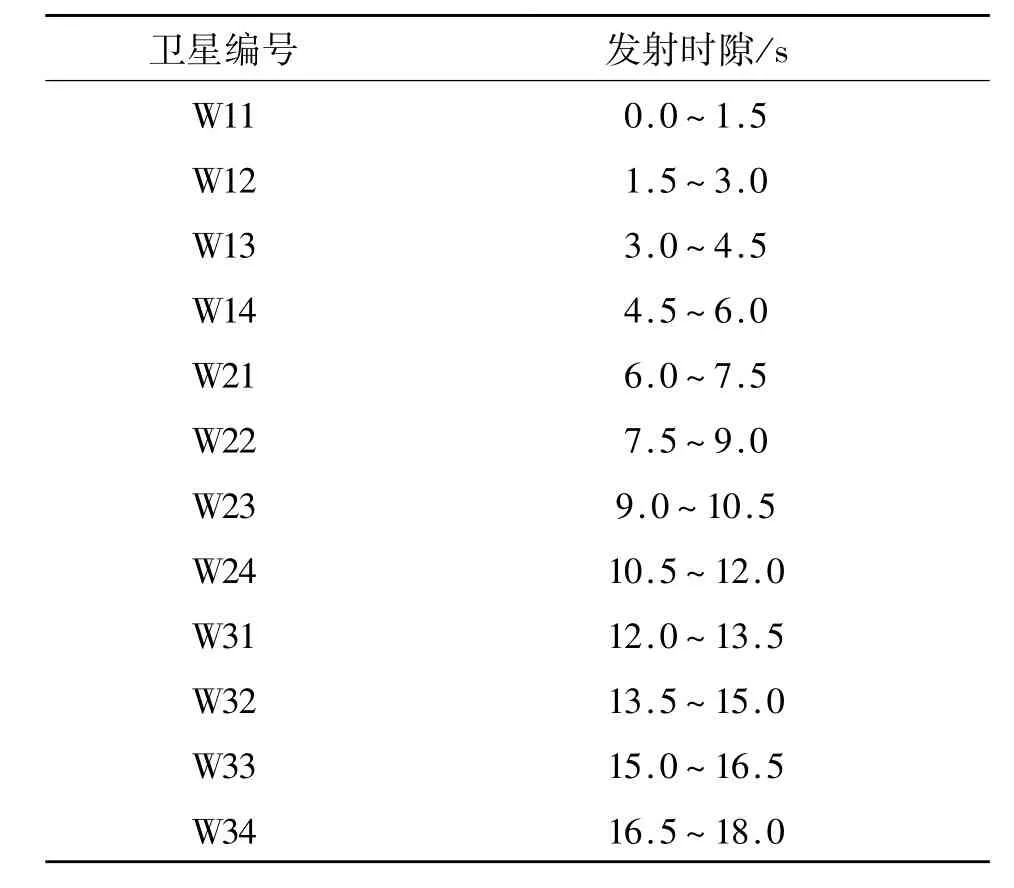
表1 星间测距信号发射时隙Table 1 The slots for transmitting inter-satel lites ranging signals

星间观测周期为5min，即每隔5min星座进行一次星间测距，星间测距的精度固定为2m（1σ）。

对于星间观测，只有可视卫星之间才进行星间测距，本文中可视的依据选择为两颗卫星连线处于电离层上方，由于电离层高度一般在60～1 000 km之间，仿真中电离层高度取为1 000 km。

由于本文主要分析联合定轨方法对UT1-UTC预报误差的抑制作用，因此在仿真过程中假定卫星的摄动力模型不存在误差，即在观测数据仿真过程中和在联合定轨处理中使用相同的摄动力模型，模型为地球非球形引力摄动（EGM96 8×8）、日月引力摄动（DE405）和太阳辐射压摄动。

仿真中对卫星初始三维位置坐标引入50m的误差。

锚固站在ECEF中的坐标为（－2160032，4383305，4085379），其对星座中所有卫星的下行导航信号在同一时刻进行星地观测，有效观测条件设置为锚固站对卫星的观测仰角大于10°，星地测距精度为可调节参数，默认值和星间观测一致。

4.2 锚固站及UT1-UTC预报误差仿真参数

使用4级傅里叶级数的Meyerhoff预报模型，并参考文献［2］使用过去一年数据进行预报的方式，分别对2005－2009年间7月1日至12月31日的UT1-UTC进行了预报，预报误差曲线如图2所示，预报误差（绝对值）最大值依次为14ms、107ms、39ms、41ms和31ms。

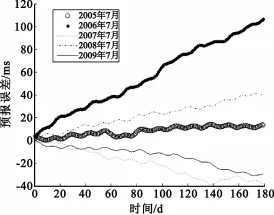
图2 UT1-UTC预报误差曲线Fig.2 The curve of the prediction error of UT1-UTC

上述结果表明，UT1－UTC预报精度有限，180天的预报误差在几十毫秒到百毫秒量级。

4.3 仿真结果

使用星座位置误差作为性能评价的参数。简记卫星i在ECEF中的真值位置矢量为XTi，估值矢量为XEi，则星座位置误差定义为

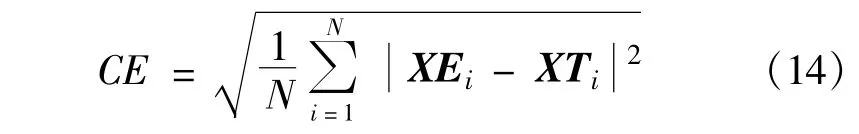
根据前文对UT1-UTC预报误差的仿真结果，选择3个典型值14ms、41ms和107ms进行自主定轨的性能仿真。

（1）无锚固站的自主定轨误差

在无锚固站的条件下，单独使用星间测量进行定轨处理，自主定轨结果如图3所示。其中，图3（a）是星座在不同UT1-UTC预报误差下的定轨误差（ECEF坐标系），图3（b）是星座在UT1-UTC预报误差为107 ms下的径向误差和水平误差（RTN坐标系）。

显然，只有星间观测时，UT1-UTC预报误差明显对定轨结果产生了影响，定轨误差随预报误差呈比例变化，误差范围和式（7）吻合。另外，对比图3（a）和（b）可以发现，UT1-UTC预报误差对卫星位置的影响主要表现在水平方向上，径向误差可以忽略。这一结论和理论分析也是一致的。由式（2）可知，UT1－UTC预报误差的影响等效为瞬时真赤道坐标系在向准地固系变换时绕Z轴旋转的角度引入了偏差，而Z轴方向的旋转显然在径向上影响较小，而在水平方向上影响较大。文献［11］从对地球定向参数的预报误差变化趋势和地球定向参数预报误差对自主定轨生成星历影响及由此给定位产生的影响的角度分析，也得出了类似的结论。

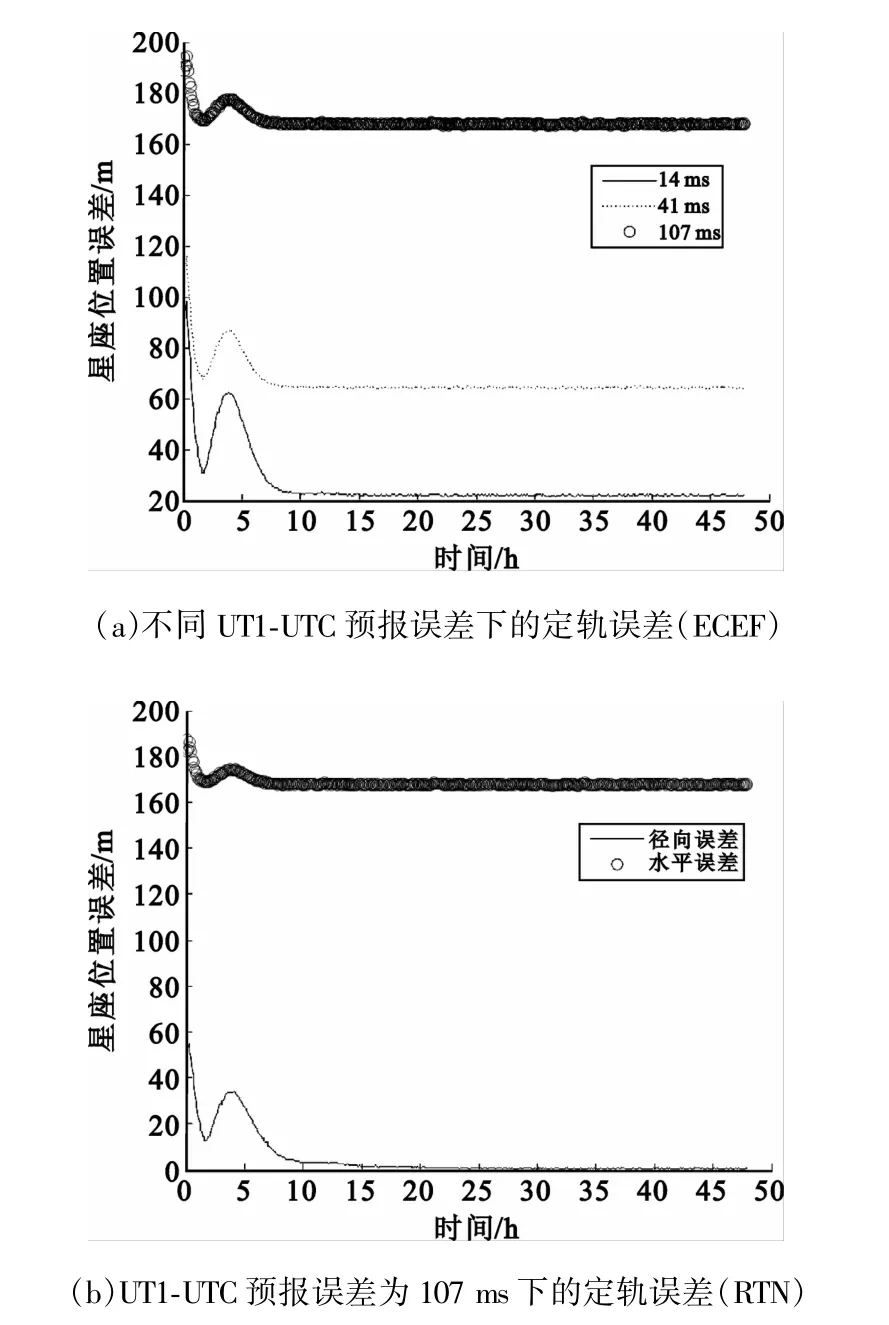
图3 单独使用星间观测量的星座自主定轨误差Fig.3 The constellation position error of using inter-satellitemeasurements only

（2）引入锚固站的自主定轨误差

引入锚固站后，联合星间和星地观测的定轨结果如图4所示。此时锚固站对星座的观测周期和观测精度均与星间观测相同，即观测周期为5min，测距精度为2m。

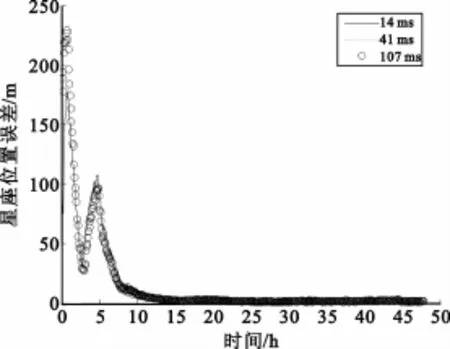
图4 联合星间和星地观测的定轨误差Fig.4 The constellation position error of using inter-satellitemeasurements and anchormeasurements

图4表明，引入锚固站后，UT1-UTC预报误差对星座的影响被有效抑制，并且在不同的UT1-UTC预报精度下，联合定轨都能获得比较好的定轨精度。

（3）改变星地观测精度

考虑到星间观测链路和星地观测链路受电离层、对流层等传播介质的影响不尽相同，如无特别的处理，星间观测链路容易实现较高的测距精度，因此本文考虑了在星地观测精度较差时的联合定轨精度。

调整星地观测精度依次为2 m、20 m和100 m，在UT1－UTC预报误差为107 ms的条件下，联合定轨结果如图5所示。

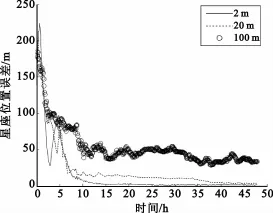
图5 不同星地观测精度条件下的联合定轨误差Fig.5 The error of combined orbit determination under different satellite-groundmeasuring accuracy

从图5可知，星座的位置误差随星地测距精度的提高而显著减小。

（4）小结

在UT1-UTC预报误差为107 ms、星间观测精度为2m的条件下，上述几种场景在仿真结束时刻（即第48 h时刻）星座位置误差汇总为表2。

表2 星座位置误差Table 2 The position error of the constellation

5 结论

UT1－UTC的预报误差对星座定轨的水平误差影响较大，如果不加以抑制，将给用户带来较大的定位误差。引入锚固站后，这一影响被有效抑制，分析和仿真结果均验证了基于锚固站的误差抑制技术的有效性，并且在位置精确已知的标校点上布设一个锚固站，在工程上也易于实现。本文的研究仅考虑了一个锚固站，对于多个锚固站的情形还需要进一步的仿真分析。

［1］Bernstein H，Bowden A F，Gartside JH.GPSUser Position Accuracy with Block IIR Autonomous Navigation［C］//Proceedings of1993 IONGPS.Salt Lake City，Utah：ION，1993：1389－1399.

［2］Ferguson JR，Duncombe R L.Modeling UT1-UTCand Polar Motion On-Board GPS Satellites［J］.Navigation：Journal of The Institute of Navigation，1984，31（3）：209－219.

［3］李征航，龚晓颖，刘万科.导航卫星自主定轨中地球定向参数误差的修正［J］.大地测量与地球动力学，2012，32（6）：71－75. LIZheng-hang，GONGXiao-ying，LIUWan-ke.Correction of Earth Orientation Parameter Error in AOD of Navigation Satellite［J］.JournalofGeodesy and Geodynamics，2012，32（6）：71－75.（in Chinese）

［4］张玉祥.人造卫星测轨方法［M］.北京：国防工业出版社，2007. ZHANG Yu-xiang.Satellite Orbit Determination［M］.Beijing：National Defense Industry Press，2007.（in Chinese）

［5］Meyerhoff SL.Error Statistics from Predicting UT1-UTC and Pole Position［R］.Dahlgren，VA：Naval Surface Weapons Center，1978.

［6］Kalarus M，Schuh H，Kosek W，et al.Achievements of the Earth orientation parameters prediction comparison campaign［J］.Journal of Geodesy，2010，84（10）：587－596.

［7］Rawicz H C，Doyle L J，Brodie PM.Apparatus and method for autonavigation with one andmore orbiting satellites and an anchor station［P］.United States：5490076，1996.

［8］Rajan JA，Brodie P，Rawicz H.Modernizing GPSAutonomous Navigation with Anchor Capability［C］//Proceedingsof2003 ION GPS.Portland，Oregon：ION，2003：1534－1542.

［9］李济生.人造卫星精密轨道确定［M］.北京：解放军出版社，1995. LI Ji-sheng.Satellite Precise Orbit Determination［M］.Beijing：People′s Liberation Army Press，1995.（in Chinese）

［10］Rajan JA.Highlights of GPS II-R Autonomous Navigation［C］//Proceedings of 2002 ION AM.Albuquerque，NM：ION，2002：354－363.

［11］张卫星，刘万科，龚晓颖.EOP预报误差对自主定轨结果影响分析［J］.大地测量与地球动力学，2011，31（5）：106－110. ZHANGWei-xing，LIUWan-ke，GONG Xiao-ying.Analysis of Influence of EOPPrediction Erroron AutonomousOrbit Determination［J］.Journal of Geodesy and Geodynamics，2011，31（5）：106－110.（in Chinese）

孟繁智（1981—），男，辽宁盖州人，2004年于国防科技大学获硕士学位，现为工程师，主要研究方向为星基导航与定位技术；

MENG Fan-zhiwas born in Gaizhou，Liaoning Province，in 1981.He received the M.S.degree from National University of Defense Technology in 2004.He is now an engineer.His research concerns satellite navigation and positioning technology.

Email：mfz9942046＠163.com

王成余（1979—），男，辽宁盖州人，2006年于中国地质大学（北京）获硕士学位，现为讲师，主要研究方向为测绘工程和地理信息系统；

WANG Cheng-yu was born in Gaizhou，Liaoning Province，in 1979.He received the M.S.degree from China University of Geosciences（Beijing）in 2006.He is now a lecturer.His research concerns surveying engineering and geographic information system.

Email：22714779＠qq.com

刘文祥（1981—），男，江西宜春人，2011年于国防科技大学获博士学位，现为讲师，主要研究方向为星基导航与定位技术；

LIUWen-xiangwas born in Yichun，Jiangxi Province，in 1981. He received the Ph.D.degree from National University of Defense Technology in 2011.He is now a lecturer.His research concerns satellite navigation and positioning technology.

Email：liuwenxiang8888＠163.com

欧钢（1969—），男，湖南株洲人，1996年于国防科技大学获博士学位，现为教授、博士生导师，主要研究方向为星基导航与定位技术。

OU Gang was born in Zhuzhou，Hunan Province，in 1969.He received the Ph.D.degree from National University of Defense Technology in 1996.He is now a professor and also the Ph.D.supervisor.His research concerns satellite navigation and positioning technology.

Email：ougangcs＠gmail.com

M itigation Technique of UT1-UTC Prediction Error Based on Anchor Ground Station

MENG Fan-zhi1，2，WANG Cheng-yu3，LIUWen-xiang1，OU Gang1
（1.School of Electronic Science and Engineering，National University of Defense Technology，
Changsha 410073，China；2.Unit95899 of PLA，Beijing 100085，China；3.Staff Room of Surveying Engineering，Yangzhou Vocational College of Environment and Resources，Yangzhou 225127，China）

The UT1－UTC prediction error is one of the error sources in the autonomous orbit determination of navigation constellation.Its influence is analyzed and its prediction accuracy is simulated.The algorithm of orbit determination is presented based on the anchor ground station.Simulations are executed with theWalker12/3/1 constellation.The results indicate the prediction error largely influences the constellation accuracy.The prediction error of 107ms brings the constellation position error of 168 m.While using the anchor，this influence is effectivelymitigated，and themitigation effect is increased with the improved accuracy of the anchor'smeasurement.

navigation constellation；coordinated universal time；anchor ground station；autonomous orbit determination；prediction error

TN967.1

A

1001－893X（2013）04－0444－06

10.3969/j.issn.1001－893x.2013.04.014

2013－03－19；

2013－04－15 Received date：2013－03－19；Revised date：2013－04－15

❋❋通讯作者：mfz9942046＠163.com Corresponding author：mfz9942046＠163.com