改进的扩展互信息分离算法❋
赵立权,蔡帮贵
(东北电力大学信息工程学院,吉林 132012)
改进的扩展互信息分离算法❋
赵立权❋❋,蔡帮贵
(东北电力大学信息工程学院,吉林 132012)
扩展互信息分离算法采用单隐层神经网络近似算法代价函数中的非线性函数,可调节的参数有限,需要多次迭代才能收敛,从而导致收敛速度较慢。针对这一问题,采用双隐层神经网络近似非线性函数,以分离结果的互信息最小化作为代价函数,采用梯度下降方法对代价函数进行优化,增加了可调节参数数量。仿真实验结果表明,改进后的算法相对原算法收敛速度更快,误差更小。
非线性独立分量分析;扩展互信息分离算法;多层感知机;双隐层神经网络
1 引言
独立分量分析(Independent Component Analysis,ICA)是在信源信号和信道参数未知的条件下,仅利用信源信号相互统计独立的性质,从观测信号中分离出信源信号的一种新的信号处理方法。目前独立分量分析的研究主要集中在线性独立分量分析的研究[1-2],但在实际的生活中遇到的更多是非线性问题,且这些问题的研究更具有实用性[3-4],为此,部分学者针对该问题提出了针对非线性混合系统的独立分量分析方法即非线性独立分量分析,并涌现出一些优秀的非线性独立分量分析算法[3-10],其中,以后置非线性独立分量分析算法最为典型[7],此后在此基础上涌现出许多改进算法[8-10]。
互信息分离(Mutual Information Separation,MISEP)算法[8]是在后置非线性独立分量分析算法的基础上提出来的,该算法以分离信号的互信息量最小化为代价函数,实现从观测信号中分离出信源信号。后来部分学者针对该算法中存在的问题提出了许多改进的算法[9-10],其中,Sun在其基础上给出了更符合实际的系统混合模型,并提出了扩展的互信息分离算法(Extended Mutual Information Separation,EMISEP)[9]。该算法仍然以分离信号的互信息最小为代价函数,采用单隐层神经网络对代价函数进行求解,分离出信源信号。由于单隐层神经网络可调节参数有限,收敛时所需迭代次数过多,导致收敛速度缓慢,针对该问题,本文提出了改进的EMISEP算法,该算法采用双隐层神经网络近似非线性函数,增加了可调节参数数量,提高了算法的收敛速度,并且在相同条件下,本文算法的分离信号与信源信号的互相关系数更大,即误差更小。
2 EM ISEP算法
EMISEP算法是在MISEP算法基础上提出的一种改进的非线性ICA算法。EMISEP算法主要是对MISEP算法的混合模型进行改进。MISEP算法的混合模型是典型的后置非线性混合模型,而EMISEP算法的模型是后置非线性线性混合模型,该模型更接近于实际情况,其混合模型如图1所示。

图1 EMISEP算法系统混合模型Fig.1 System mixedmodel of EMISEP algorithm
图中S=[s1,s2,…,sn]T是信源信号,U是线性混合矩阵,F=[F1,F2,…,Fn]是可逆的非线性函数,V是线性混合矩阵,X=[x1,x2,…,xn]T是混合信号即观测信号,n是信源号数量,为了方便,一般假设观测信号的数量和信源信号的数量相等。该模型的数学表达式如下:

EMISEP算法信号分离模型如图2所示。

图2 EMISEP算法信号分离模型Fig.2 Signal separationmodel of EMISEP algorithm
图2中,C、g、D和ψ共同模块构成分离系统,C和D是线性解混矩阵,g是非线性解混函数,ψ是对分离系统起辅助作用的非线性函数,y=[y1,y2,…,yn]T是分离系统对信源信号的估计,z=[z1,z2,…,zn]T是分离信号经过非线性函数ψ得到的输出信号,EMISEP算法以输出信号z的信息最大化为代价函数。
由于z是y的非线性变换,则z和y的信息量是相等的,即:

式中,I()代表互信息量,H()代表熵。当选取的非线性函数ψ等于y的累积概率函数时,Zi在[0,1]上服从均匀分布,此时H(zi)=0,则上式简化成如下公式:
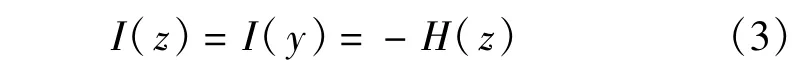
当估计信号Y的各分量相互统计独立时,此时互信息量I(y)最小,由式(3)可知此时H(z)最大,即此时z的信息量达到最大化,因此EMISEP以信息最大化为代价函数。
由图2我们可以得出z的联合概率密度为
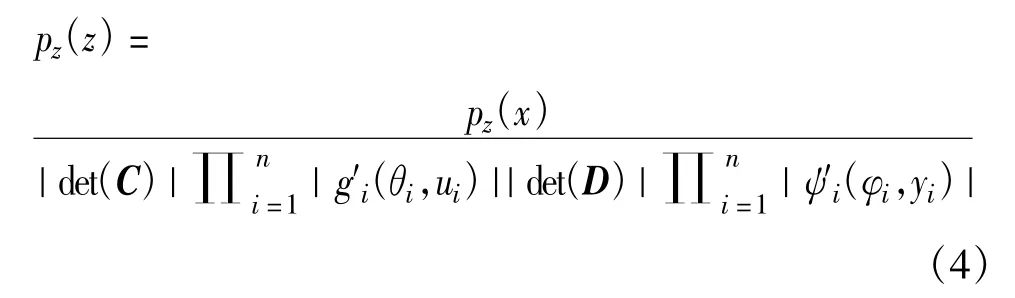
式中,det(·)是计算矩阵的行列式,θi和φi分别是gi和ψi中的参数。因此,z的联合熵为

采用梯度下降方法对其进行优化,可得


EMSIEP算法采用两组感知机来近似非线性函数gk(θk,uk)和ψk(φk,yk)。其中:

式中,Mk表示感知机隐层节点数目,ξk和ωk表示输入层和输出层的权值,σ()表示激活函数。
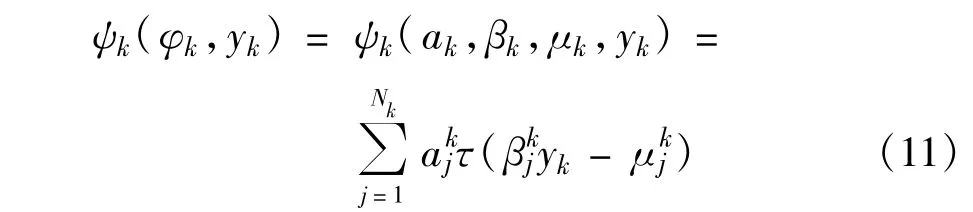
式中,Nk表示感知机隐层节点数目,ak和βk表示输入层和输出层的权值,τ()表示激活函数。
为了得到最大的输出熵,由公式(5)可知代价函数可以改写为
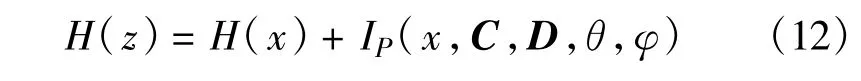
其中:

由于H(x)在学习过程中没改变,所以在迭代过程中用IP(x,C,D,θ,δ)作为目标函数。用Ip从t到t+1时刻的变化量Er作为迭代停止的判断条件,如果Er比预先设置的门限ϑ小那么就停止迭代。
3 改进的EM ISEP算法
改进算法是在原算法的基础上增加一层隐含层,使优化问题的可调节参数数量增加。除第二个隐含层增加了6个节点外,其他参数都与文献[9]相同。改进算法的分离模型如图3所示。
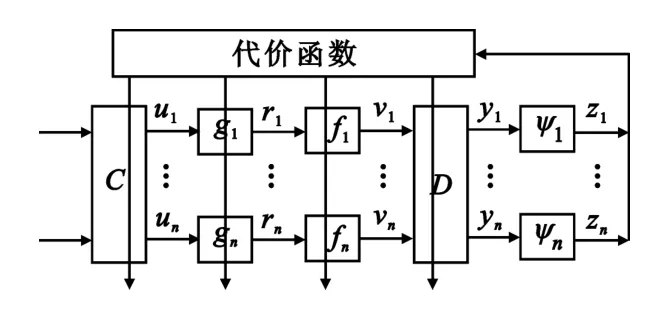
图3 改进算法的分离模型Fig.3 Separationmodel of improved algorithm
相对图2的解混系统,新算法在解混非线性模块g=[g1,g2…gn]T之后增加了一层隐含层f=[f1,f2,…,fn]T。因此,z的联合熵为

采用梯度下降方法对上式进行优化,由于H(x)在分离系统中不包含任何参数,因此其梯度为零。其他参数的梯度表达式如下:

采用3组感知机来模拟非线性函数gk(θk,xk)、fk(hk,rk)和ψk(φk,yk),其中:

式中,Ok表示感知机隐层节点数目,pk和ek表示输入层和输出层的权值,λ()表示激活函数。gk(θk,xk)和ψk(φk,yk)参数具体含义参见公式(10)和(11)。采用梯度下降方法对分离系统参数进行估计,即:
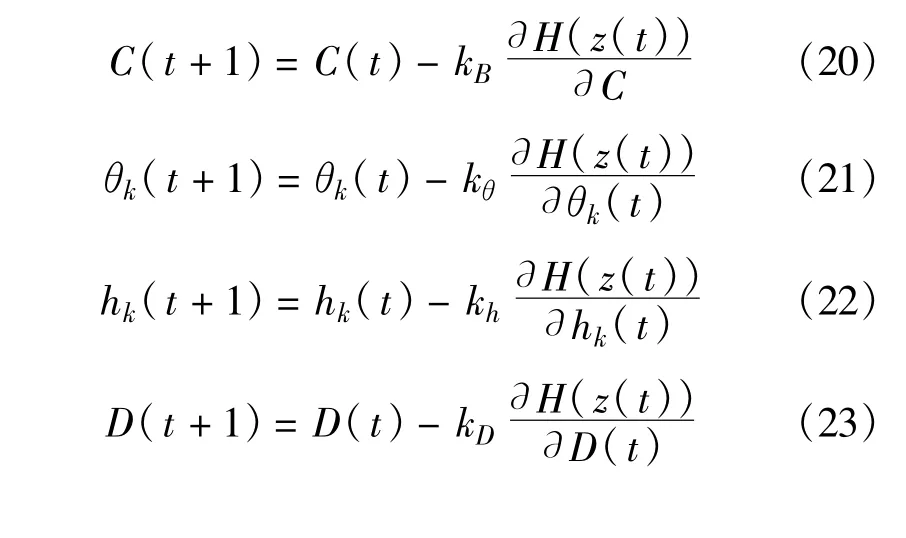

式中,k是迭代步长,θk=(ξk,ωk,ηk),hk=(lk,pk,ek),ψk=(ak,βk,μk)。分离系统参数梯度计算公式如下:

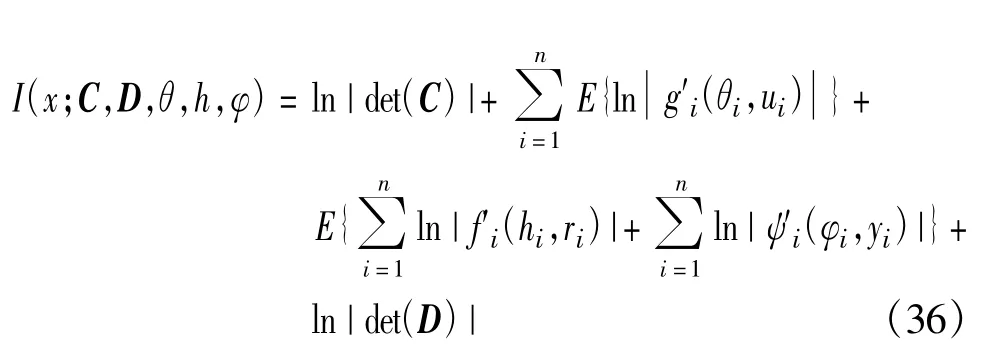
由公式(13)可知,H(z)的最大化与H(x)无关,因此,最大化H(z)等效于最大化式(36),则改进的EMISEP算法流程如下:
(1)对参数C,D,θ,h,φ进行初始化;
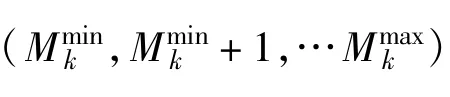
(3)根据公式(20)~(35)调整分离系统参数;
(4)根据公式(36)计算I(x;C,D,θ,h,φ),如果|I(x;C,D,θ,h,φ)(t+1)-I(x;C,D,θ,h,φ)(t)|的值小于预设误差门限,则算法停止迭代,算法收敛,否则返回到第3步。
4 仿真实验
为了验证本文算法的有效性,采用两个信号作为信源信号,其数学表达式如下:

图1中线性混合矩阵为随机产生的固定混合矩阵:

图1中的非线性函数f为双曲正切函数。图1中的线性混合矩阵V为随机产生的固定混合矩阵:

则混合信号为X=V tanh(US)。
系统各部分波形仿真如图4所示,其中,图4(a)是信源信号,图4(b)是经过图1的混合系统得到的混合信号即观测信号,图4(c)是本文算法从混合信号中分离出的信号,图4(d)是EMISEP算法从混合信号中分离出的信号。从图4(c)中可以看出,本文算法分离出的信号和信源信号的波形更接近,仅是幅值不同(这一点是ICA固有的问题,并不影响实际应用),因此图4(c)证明了本文算法是有效的。
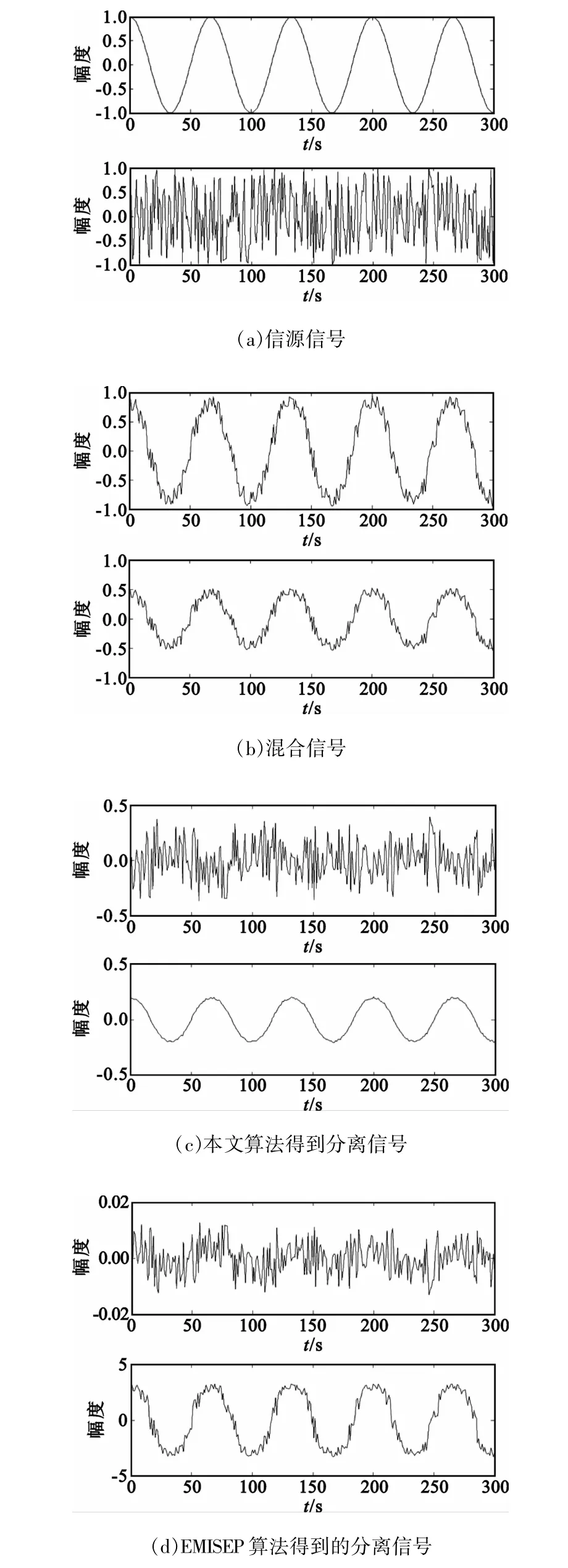
图4 系统各部分波形Fig.4 Signalwaveforms of the whole system
为了验证本文算法的收敛速度,在相同条件下,对EMISEP算法和本文算法进行了仿真对比,对比结果如图5所示。图5的横坐标是时间,单位是秒,纵坐标是分离信号与信源信号的互相关系数,互相关系数越大代表分离信号与信源信号的相似度高,意味着误差越小,分离效果越好。从图5中可以看出,本文算法在1.099 s时相关系数已经趋于平稳,而EMISEP算法在1.25 s时相关系数才趋于平稳,因此证明了本文算法的收敛速度比较快,而且算法收敛时,本文算法的相关系数为0.964 9,EMISEP算法的相关系数为0.926 9,证明了本文算法的误差更小,分离效果好于EMISEP算法。
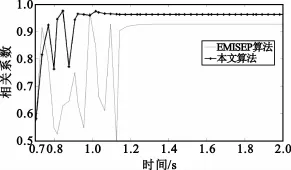
图5 算法性能对比Fig.5 Comparison of the algorithms performance
5 结论
本文针对EMISEP算法收敛速度慢的问题,提出了基于多隐层神经网络的改进的EMISEP算法。相对原算法,改进后的算法虽然增加了算法的复杂度,但在相同条件下,该算法收敛时需要的迭代次数更少,总体收敛时间更短,而且相对原EMISEP算法,改进后的算法收敛时的相关系数更大,也就是分离信号更接近信源信号,误差更小。
[1]Hyvarinen A,Karhunen J.Independent component analysis[M].New York:Wiley,2001.
[2]马守科,何选森,许广廷.基于扩展Infomax算法的变步长在线盲分离[J].系统仿真学报,2007,19(19):4513-4516. MA Shou-ke,HE Xuan-sen,XU Guang-ting.Variable step size extended Infomax Algorithm-based online blind separation[J].Journal of System Simulation,2007,19(19):4513-4516.(in Chinese)
[3]Tan Y,Jun W.Nonlinear Blind Source Separation Using a Radial Basis Function Network[J].IEEE Transactions on Neural Networks,2001,12(1):124-134.
[4]Xiaoren D,Ma Ye.Extracting post-nonlinear signalwith reference[J].Computers and Electrical Engineering,2011,37(6):1171-1181.
[5]方勇,王明祥.基于自组织映射的后非线性独立分离分析的初始化方法[J].电子学报,2005,5(33):889-892.FANG Yong,WANGMing-xiang.Based on the self-organizing mapping nonlinear independent after separation analysis method for initialization[J].Electronic Journal,2005,5(33):889-892.(in Chinese)
[6]Chunhou Z,Deshuang H.MISEPMethod for Post-nonlinear blind source separation[J].Neural Computation,2007,19(19):2557-2578.
[7]Taleb A,Jutten C.Source Separation in Post-Non linearMixtures[J].IEEE Transactions on Signal Processing,1999,47(10):2807-2820.
[8]Almeida L B.MISEP-Linear and Nonlinear ICA Based on Mutual Information[J].Journal of Machine Learning Research,2003,12(4):1297-1318.
[9]lisun Z.An Extension of MISEP for Post-non linear-linear Mixture Separation[J].IEEE Transactions on Circuits and Systems,2009,56(8):654-658.
[10]Clemente RM,Mellado SH,Acha JI.MLP-based source separation for MLP-like nonlinearmixtures[C]//Proceedings of the 4th International Symposium on Independent Component Analysis and Blind Signal Separation.Nara,Japan:IEEE,2003:155-160.

赵立权(1982—),男,黑龙江哈尔滨人,2005年于哈尔滨理工大学获工学学士学位,2009年于哈尔滨工程大学获工学博士学位,现为副教授、硕士生导师,主要研究方向为独立分量分析;
ZHAO Li-quan was born in Harbin,Heilongjiang Province,in 1982.He received the B.S. degree from Harbin University of Science and Technology and the Ph.D.degree from Harbin Engineering University in 2005 and 2009,respectively.He is now an associate professor and also the instructor of graduate students.His research concerns independent componentanalysis.
Email:zhao-liquan@163.com
蔡帮贵(1987—),男,四川自贡人,2011年于海南师范大学获工学学士学位,现为硕士研究生,主要研究方向为非线性独立分量分析。
CAIBang-guiwasborn in Zigong,Sichuan Province,in 1987. He received the B.S.degree from Hainan Normal University in 2011.He is now a graduate student.His research concerns nonlinear independent component analysis.
Extended M utual Information Separation Algorithm s Based on M ulti-Hidden Layer
ZHAO Li-quan,CAIBang-gui
(College of Information Engineering,Northeast Dianli University,Jilin 132012,China)
Extendedmutual information separation(EMISEP)algorithm uses a single hidden layer neural network to approximate nonlinear function of cost function,so the adjustable parameter is limited and itneedsmore iteration times to converge,which leads to relatively slow convergence speed.To overcome this problem,this paper uses double hidden layer perceptions to approximate nonlinear function of cost function,and usesmutual informationminimum of separation signals as cost function,which is optimized by gradient descentmethod.This increases the number of adjustable parameters.The simulation results prove that the improved algorithm has faster convergence speed and smaller error comparingwith the original algorithm.
nonlinear independent component analysis;extendedmutual information separation algorithm;multilayer perception;double hidden layer neural network
TN911.7
A
1001-893X(2013)04-0402-06
10.3969/j.issn.1001-893x.2013.04.006
2012-10-05;
2013-01-28 Received date:2012-10-05;Revised date:2013-01-28
吉林省科技发展计划项目(201101110)
Foundation Item:The Scientific Research Fundation of the Education Department of Jilin Province(No.201101110)
❋❋通讯作者:zhao-liquan@163.com Corresponding author:zhao-liquan@163.com
——以鲁甸地震相关新浪微博为例

