基于约束加权最小二乘的时差频差联合定位算法❋

朱华进，张 洋，鄂 嵋，禹华钢

（1.解放军91469部队，北京 100841；2.海军司令部军务部，北京 100841；3.解放军91033部队，山东青岛 266071）

基于约束加权最小二乘的时差频差联合定位算法❋

朱华进1，❋❋，张 洋2，鄂 嵋3，禹华钢1

（1.解放军91469部队，北京 100841；2.海军司令部军务部，北京 100841；3.解放军91033部队，山东青岛 266071）

针对运动目标源定位问题，提出了一种基于约束加权最小二乘（Constrained Weighted Least-Squares，CWLS）的时差频差定位算法。该算法利用目标源到达多个接收站的时差和频差信息，对目标源的位置和速度进行估计。通过引入中间变量，将时差频差非线性方程转换成伪线性方程（中间变量与目标源位置和速度之间存在约束关系），再对此约束条件引入拉格朗日乘子技术，将此伪线性方程的求解转化为求条件极值问题，创造性地求解了此非线性定位方程，提高了定位精度，并能满足实时性和全局收敛要求。仿真实验表明，该算法在保持相近复杂度的同时，进一步提高了定位性能，优于两步加权最小二乘算法，在噪声较高时仍然能达到克拉美罗下限。

目标源定位；约束加权最小二乘；到达时差；到达频差；拉格朗日乘子技术

1 引言

目标源定位技术在雷达［1－2］、声纳［3］、导航、无线通信、传感器网络［4－5］等领域有着广泛的应用，一直是信号处理领域的研究热点之一。对于静止或静态目标源和接收机情况下的无源定位问题，通常的思路是估计目标源到空间分散的接收机或传感器的到达时差（Time Difference of Arrival，TDOA）来进行定位。现代定位系统中，接收机往往被安装在飞机、卫星、空中无人飞行器等运动平台上［6］，当目标源与接收机之间存在相互运动时，多普勒频差（Frequency Difference of Arrival，FDOA）定位技术可以与TDOA定位技术相结合，能同时估计出目标源的位置和运动速度，并能有效地提高定位精度［7－9］。

2004年，Ho等人对运动目标源的TDOA/FDOA联合定位技术进行了深入分析，建立了完善的理论体系，当已知接收站位置、速度和信号传播速度时，运动目标源定位问题可以用TDOA/FDOA非线性方程来表示，并提出了著名的两步加权最小二乘（twostep Weighted Least-Squares，two-step WLS）TDOA/FDOA联合定位算法［10］。不同于传统的线性迭代方法［11］，two-step WLS算法通过引入中间变量将TDOA/FDOA非线性定位方程转化为伪线性方程（中间变量与目标源之间存在约束关系），从而可以求解其代数解，避免了初始点选择和不收敛问题，在较高信噪比时能达到克拉美罗下限（Cramér-Rao Lower Bound，CRLB）［10］。在此基础上，本文提出了一种基于约束加权最小二乘（Constrained Weighted Least-Squares，CWLS）的TDOA/FDOA联合定位算法，该算法在WLS方程的基础上，通过引入拉格朗日乘子技术，将此伪线性方程的求解转化为求条件极值问题，并采用多项式求根运算来求解此拉格朗日乘子，保证了算法的实时性和全局收敛。更重要的是，该算法在较高噪声时仍然能达到CRLB，克服了two-step WLS算法在噪声较高时性能衰减的缺点。

2 运动目标源定位问题

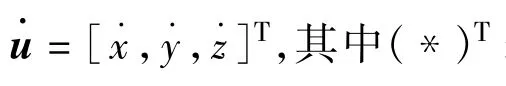
根据上述定义，目标源到接收站的真实距离为

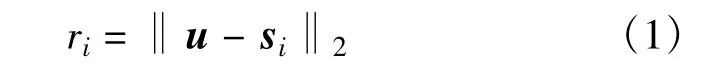
其中，‖*‖2表示求2范数，i＝1，2，…，M。则目标源到达基准站与其他站之间的距离差为

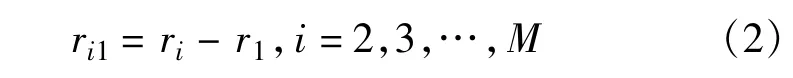
为有效利用FDOAs，对式（2）求时间微分：

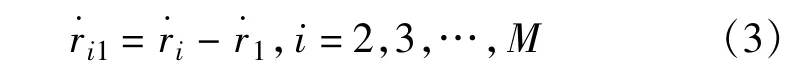
其中，通过对式（1）求时间微分，能得到˙ri的表达式：

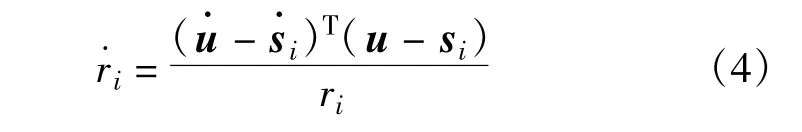
在实际应用中，观测得到的TDOAs：Td＝［t21，t31，…，tM1］T和FDOAs：Fd＝［f21，f31，…，fM1］T中都存在加性噪声。当信号传播速度恒定时，距离差及其对时间的微分分别与TDOA和FDOA之间成比例关系，则观测到的距离差及其对时间的微分分别可以表示为［7］

3 基于CWLS的TDOA/FDOA定位算法

首先定义辅助向量

将ri和r1的表达式代入ri＝ri1＋r1，并对此方程两边同时求平方，得到TDOA方程：

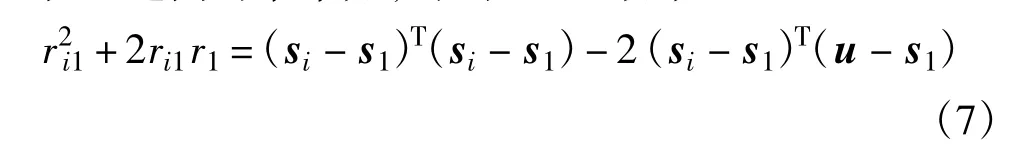
对式（7）求时间微分，可得到相应的FDOA方程：

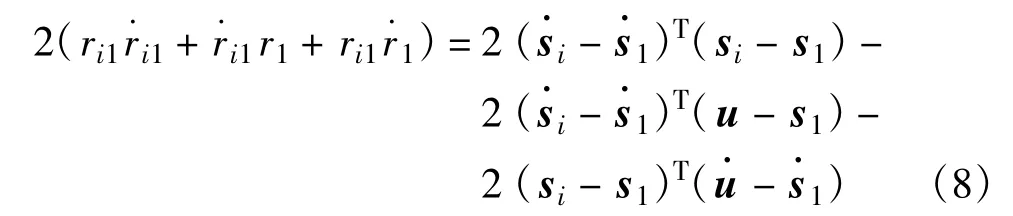
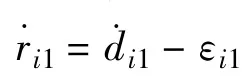
并忽略二阶误差项，可得式（9）、（10）：

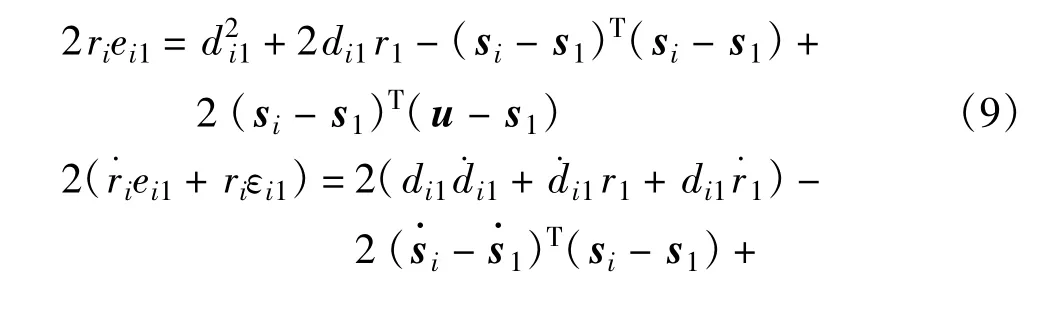
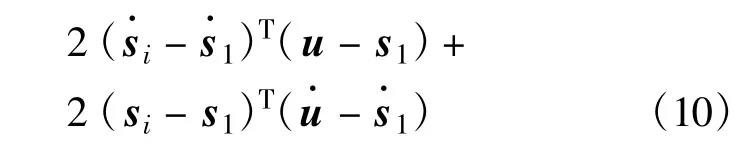
综合式（9）、（10）得到对应的矩阵表达形式：

其中：

对θ进行估计时，必须考虑此约束关系。

首先，对式（11）求WLS解［13］：

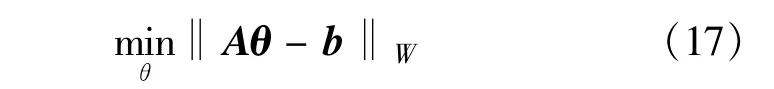
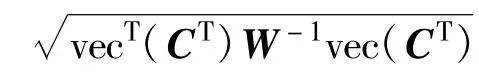
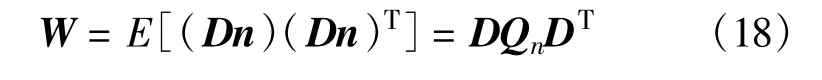
式中，Qn＝E［nnT］为TDOA/FDOA噪声向量n的协方差矩阵。

将约束条件式（15）、（16）代入式（18），则CWLS解等价于对式（19）求最小化：

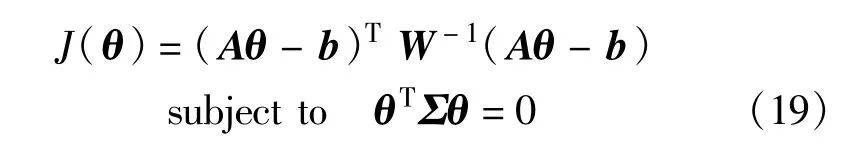
采用拉格朗日乘子技术来求解此条件极值问题，式（19）等同于

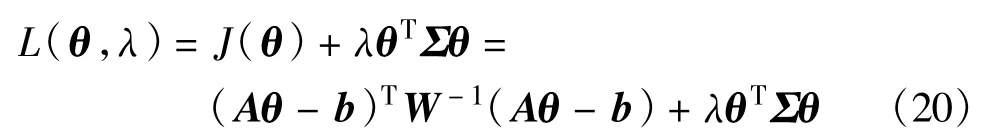
对式（21）进行求解得到

式中，拉格朗日乘子λ仍然有待求解。将式（22）代入约束条件θTΣθ＝0来求解拉格朗日乘子λ。

其中，I8为8×8的单位矩阵。对矩阵ATW－1AΣ－1进行特征值分解：

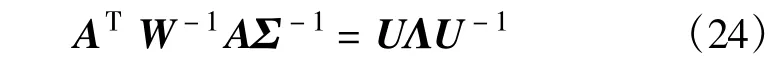
其中，Λ＝diag｛η1，η2，…，η8｝为对角矩阵。将式（24）代入式（23）得到方程

其中，p＝［p1，p2，…，p8］T＝UTΣ－TATW－1b，q＝［q1，q2，…，q8］T＝U－1ATW－1b。

式（25）是一个14阶的多项式方程。不同于文献［14－16］以0为初始点，分别采用切线法和牛顿迭代法对式（25）进行求解，本文通过卷积运算对式（25）进行化简，能简便地求得此多项式f（λ）的各阶系数，得到一个14阶的标准多项式方程，再通过多项式求根运算，能快捷地求解此多项式方程的根。

综上所述，基于CWLS的TDOA/FDOA定位算法的流程如下：

（1）定义W＝IM－1；

（2）通过卷积运算（对应MATLAB中命令“conv”）将f（λ）转化为标准多项式，通过多项式求根运算（对应MATLAB中命令“roots”）求解此多项式方程，考虑到拉格朗日乘子λ为实数，只需保留其中的实数根；

第4节中的仿真实验表明，重复执行步骤2和步骤3两次就能得到足够精确的解＾θ。

4 仿真实验

为验证本文算法的性能，对近距离目标源和远距离目标源分别进行了一系列的蒙特卡罗仿真实验。从定位偏差、定位精度和计算复杂度3个方面对本文提出的CWLS算法与two-step WLS算法［10］的性能进行了比较，其中two-step WLS算法进行了两次迭代运算。在仿真实验中，设定目标源位置单位为m，速度单位为m/s。

为保证仿真实验的有效性，采用与文献［10］相同的接收站几何分布和目标源位置，如表1所示。

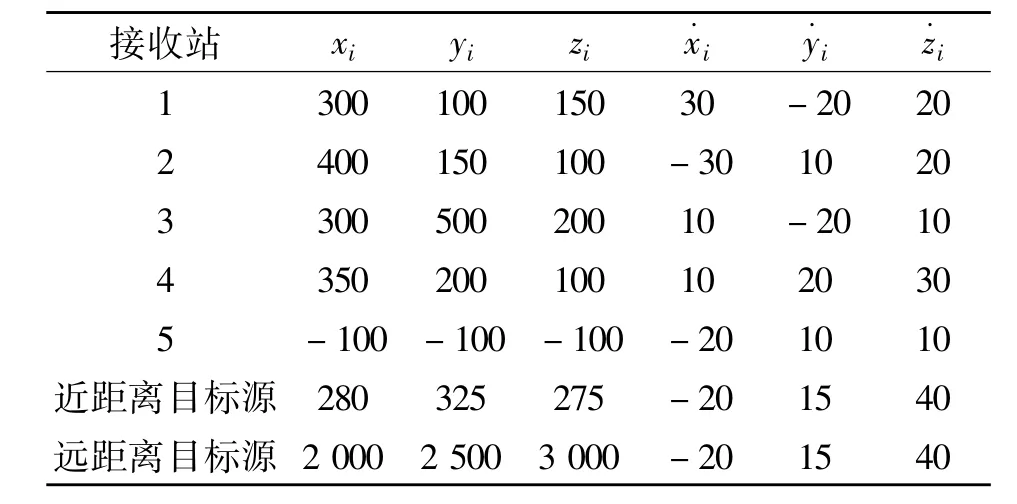
表1 接收站和目标源的位置和速度Table 1 Positions and velocities of receivers

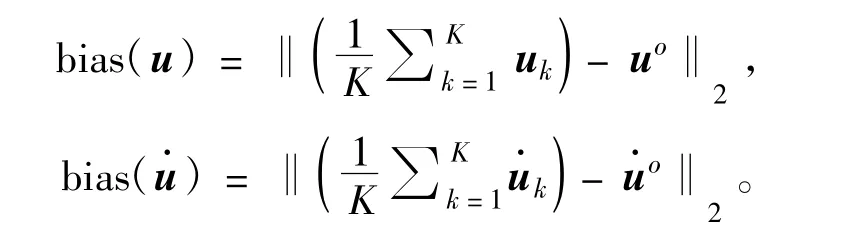
采用误差均方根（Root Mean Squares Error，RMSE）来度量对目标源位置和速度的定位精度，分别定义为

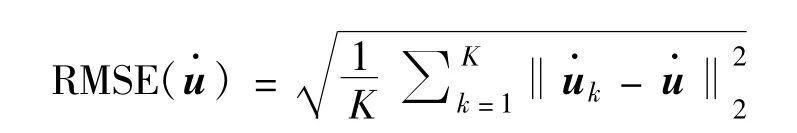
首先对近距离目标源的定位问题进行仿真实验分析。如图1和图2所示，本文提出的CWLS算法的定位偏差远低于two-step WLS算法，且在高噪声条件时尤其明显。当噪声较低时，CWLS算法的定位偏差接近为0，证明了CWLS在噪声较低时是渐近无偏的估计算法。同时，由于定位方程的非线性本质，随着噪声的增大，两种算法的定位偏差都有所增大，但CWLS算法的定位偏差增大速度明显低于two-step WLS算法。

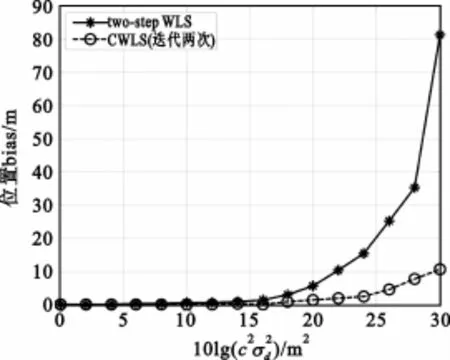
图1 不同噪声强度条件下对近距离目标位置偏差的比较Fig.1 Comparison of the position bias of the proposed estimatorwith the two-step WLSmethod versus measurement error for near-field source

图2 不同噪声强度条件下对近距离目标速度偏差的比较Fig.2 Comparison of the velocity bias of the proposed estimatorwith the two-step WLSmethod versus measurement error for near-field source

图3和图4以CRLB为基准，给出了two-step WLS和CWLS算法定位精度随测量误差变化曲线，其中采用RMSE来度量定位精度。当噪声高于6 dB时，two-step WLS算法性能开始发散，不能达到CRLB，而CWLS算法在噪声低于16 dB都可以到达CRLB。这表明CWLS算法随噪声增大而性能发散的门限比two-step WLS算法高10 dB，这一性能在较高噪声条件下具有显著的优势。

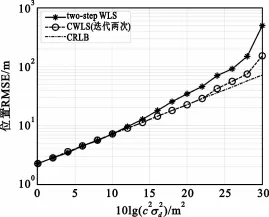
图3 不同噪声强度条件下对近距离目标位置RMSE的比较Fig.3 Comparison of the position RMSE of the proposed estimatorwith the two-step WLSmethod versus measurement error for near-field source

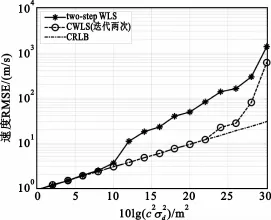
图4 不同噪声强度条件下对近距离目标速度RMSE的比较Fig.4 Comparison of the velocity RMSE of the proposed estimatorwith the two-step WLSmethod versus measurement error for near-field source

图5～8分别给出了对远距离目标源定位偏差和精度随测量误差变化曲线，可以看出本文提出的CWLS算法比two-step WLS算法具有更好的性能。

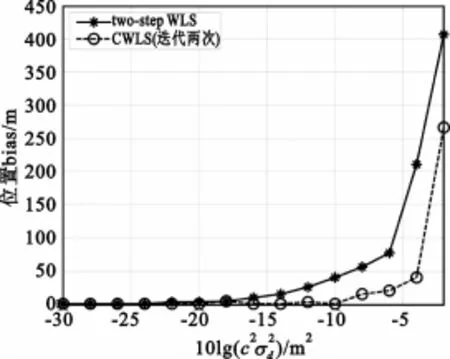
图5 不同噪声强度条件下对远距离目标位置偏差的比较Fig.5 Comparison of the position bias of the proposed estimatorwith the two-step WLSmethod versus measurementerror for far-field source

图6 不同噪声强度条件下对远距离目标速度偏差的比较Fig.6 Comparison of the velocity bias of the proposed estimatorwith the two-step WLSmethod versus measurementerror for far-field source

图7 不同噪声强度条件下对远距离目标位置RMSE的比较Fig.7 Comparison of the position RMSE of the proposed estimatorwith the two-step WLSmethod versus measurementerror for far-field source

图8 不同噪声强度条件下对远距离目标速度RMSE的比较Fig.8 Comparison of the velocity RMSE of the proposed estimatorwith the two-step WLSmethod versus measurementerror for far-field source

采用MATLAB软件进行10 000次仿真实验，twostep WLS和CWLS算法所需的运算时间分别为18.132 5 s和34.468 3 s，表明两种定位算法均能满足实时性要求。

由于two-step WLS算法首先不考虑中间变量与目标源位置和速度之间的约束关系，直接将伪线性方程当作线性方程，求解其WLS解，再在第二步时单独考虑此约束关系，来对定位结果进行修正，在噪声较低时具有很好的性能，但当噪声较大时，则会造成性能的发散。而本文提出的CWLS算法通过引入拉格朗日乘子技术，将此约束关系转化为条件极值问题，自始至终都考虑了此约束关系，因此具有更好的性能。由于CWLS算法需要求取拉格朗日乘子，其中包括了特征值分解运算、高阶多项式求根等运算，故其计算复杂度稍高于two-step WLS算法，但仍然能满足实时性要求。仿真结果与理论分析相符合。在实际应用中，如果噪声分布无法精确估计，以上两种算法均无法达到仿真结果中的性能，但仍然能有效改善对目标的定位精度。

5 结论

现代定位系统中，接收机往往被安装在飞机、卫星、空中无人飞行器等运动平台上，能实现对运动目标的精确定位。针对这一定位问题，本文提出了一种基于CWLS的TDOA/FDOA联合定位算法。仿真实验表明，该算法和two-step WLS算法复杂度相近，能满足实时性要求，性能却远优于后者，CWLS算法的噪声门限比two-step WLS算法高10 dB，在噪声较高时具有很好的性能，具有显著的优势。在后续研究中，将考虑接收站自身定位存在误差对目标定位精度的影响，并提出相应解决办法。

［1］晁淑媛，陈伯孝，杨明磊，等.MIMO与MISO雷达定位精度分析［J］.电子与信息学报，2011，33（1）：60－65. CHAO Shu-yuan，CHEN Bai-xiao，YANG Ming-lei，et al. Study of localization of MIMO and MISO radars［J］.Journal of Electronics＆Information Technology，2011，33（1）：60－65.（in Chinese）

［2］Norouzi Y，Derakhshani M.Joint time difference of arrival/angle of arrival position finding in passive radar［J］.IET Radar，Sensor and Navigation，2009，3（2）：167－176.

［3］刘文海，王逸林.水下被动定位声纳显示及航迹跟踪方法［J］.声学技术，2010，29（1）：99－102. LIUWen-hai，WANG Yi-lin.Research on the display and trajectory tracking methods for passive ranging sonar［J］. Technical Acoustics，2010，29（1）：99－102.（in Chinese）

［4］盛卫东，龙云利，周一宇.天基光学传感器网络目标定位精度分析［J］.光学学报，2011，31（2）：247－253. SHENGWei-dong，LONGYun-li，ZHOUYi-yu.Analysisof target location accuracy in space-based optical-sensor network［J］.Acta Optica Sinica，2011，31（2）：247－253.（in Chinese）

［5］黄大庆，诸燕平.一种无线传感器网络自身节点定位算法［J］.华中科技大学学报（自然科学版），2010，38（10）：80－84. HUANG Da-qing，ZHU Yan-ping.A node self-location method in wireless sensor networks［J］.Journal of Huazhong University of Science And Technology（Nature Science Edition），2010，38（10）：80－84.（in Chinese）

［6］Sun M，Ho K C.An asymptotically efficient estimator for TDOA and FDOA positioning ofmultiple disjointsources in the presence of sensor location uncertainties［J］.IEEE Transactions on Signal Processing，2011，59（7）：3434－3440.

［7］Ho K C，Lu X，Kovavisaruch L.Source localization using TDOA and FDOA measurements in the presence of receiver location errors：Analysis and solution［J］.IEEE Transactions on Signal Processing，2007，55（2）：684－696.

［8］朱伟强，黄培康，马琴，等.多站时差频差高精度定位技术［J］.数据采集与处理，2010，25（3）：307－312. ZHUWei-qiang，HUANG Pei-kang，MA Qin，et al.Emitter location with multi-station using TDOA/FDOA measurements［J］.Journal of Data Acquisition＆Processing，2010，25（3）：307－312.（in Chinese）

［9］郭福成，樊昀.双星时差频差联合定位方法及其误差分析［J］.宇航学报，2008，29（4）：1381－1386. GUOFu-cheng，FAN Yun.A method of dual-satellites geolocation using TDOA and FDOA and its precision analysis［J］.Journal of Astronautics，2008，29（4）：1381－1386.（in Chinese）

［10］Ho K C，Xu W.An accurate algebraic solution formoving source location using TDOA and FDOA measurements［J］. IEEE Transactions on Signal Processing，2004，52（9）：2453－2463.

［11］FoyW H.Position-location solution by Taylor-series estimation［J］.IEEE Transactions on Aerospace and Electronic Systems，1976，AES－12（2）：187－194.

［12］Yang K，An JP，Bu X Y，et al.Constrained total leastsquares location algorithm using time-difference-of-arrival measurements［J］.IEEE Transactions on Vehicular Technology，2010，59（3）：1558－1562.

［13］Markovsky I，Huffel SV.Overview of total least-squaresmethods［J］.Signal Processing，2007，87（10）：2283－2302.

［14］Huang Y T，Benesty J，Elko GW，etal.Real-time passive source localization：A practical linear-correction leastsquares approach［J］.IEEE Transactions on Speech and Audio Processing，2001，9（8）：943－956.

［15］So H C，Hui SP.Constrained location algorithm using TDOA measurements［J］.IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，2003，E86－A（12）：3291－3293.

［16］Cheung KW，So H C，MaW K，etal.A constrained leastsquares approach tomobile positioning：Algorithms and optimality［J］.EURASIP Journal Application Signal Processing，2006：150.

［17］Chan Y T，Ho K C.A simple and efficientestimator for hyperbolic location［J］.IEEE Transactions on Signal Processing，1994，42（8）：1905－1915.

朱华进（1978—），男，湖北武穴人，分别于2000年和2003年获海军工程大学学士学位和硕士学位，现为工程师，主要研究方向为通信信号处理和导航工程；

ZHU Hua-jin was born in Wuxue，Hubei Province，in 1978.He received the B.S.degree and the M.S.degree from Naval University of Engineering in 2000 and 2003，respectively.He is now an engineer. His research interests include communication signal processing and navigation engineering.

Email：82450049＠qq.com

张洋（1983—），女，山东青岛人，2007年于海军工程大学获学士学位，现为硕士研究生，主要研究方向为信号处理和信息处理；

ZHANG Yang was born in Qingdao，Shandong Province，in 1983.She received the B.S.degree from Naval University of Engineering in 2007.She is now a graduate student.Her research interests include signal processing and information processing.

Email：63846660＠qq.com

鄂嵋（1981—），女，黑龙江讷河人，2011年于海军工程大学获学士学位，现为助理工程师，主要研究方向为信号处理和信息处理；

EMeiwas born in Neihe，Heilongjiang，in 1981.She received the B.S.degree from Naval University of Engineering in 2011.She is now an assistant engineer.Her research interests include signal processing and information processing.

Email：63846660＠qq.com

禹华钢（1984—），男，湖南邵东人，分别于2006年、2008年和2012年获海军工程大学工学学士学位、硕士学位和博士学位，现为工程师，主要研究方向为无源定位、通信信号处理、通信工程。

YU Hua-gangwasborn in Shaodong，Hunan Province，in 1984. He received the B.S.degree，the M.S.degree and the Ph.D.degree from Naval University of Engineering in 2006，2008 and 2012，respectively.He is now an engineer.His research interests include passive detection，communication signal processing and communication engineering.

Email：yu－huagang＠hotmail.com

Constrained W eighted Least-Squares Algorithm for M oving Source Location Using TDOA and FDOA M easurements

ZHU Hua-jin1，ZHANG Yang2，EMei3，YU Hua-gang1
（1.Unit91469 of PLA，Beijing 100841，China；2.Military Affairs Department of Naval Headquarters，Beijing 100841，China；3.Unit91033 of PLA，Qingdao 266071，China）

By utilizing the time difference of arrival（TDOA）and frequency difference of arrival（FDOA）measurements of a signal received ata number of receivers，a constrained weighted least-squares（CWLS）algorithms for estimating the position and velocity of a moving source is proposed.By utilizing the Lagrange multipliers technique，the known relation between the intermediate variables and the source location coordinates can be exploited to constrain the solution.And，on basis of convolute and polynomial rooting operations，the Lagrange multipliers can be obtained efficiently and robustly，which can allow real-time implementation aswell as ensure global convergence.Simulation results show that the proposed estimator achieves remarkably better performance than the two-step weighted least squares（WLS）approach especially for highermeasurement noise level，which makes the Cramér-Rao lower bound（CRLB）at a sufficiently high noise level before the threshold effect occurs possible.

source localization；constrained weighted least-squares（CWLS）；time difference ofarrival（TDOA）；frequency difference of arrival（FDOA）；Lagrangemultipliers

TN97；V556

A

1001－893X（2013）04－0395－07

10.3969/j.issn.1001－893x.2013.04.005

2012－10－15；

2013－02－27 Received date：2012－10－15；Revised date：2013－02－27

国家高技术研究发展计划（863计划）项目（2010AA7010422）

Foundation Item：The National High-tech R＆D Program of China（863 Program）（2010AA7010422）

❋❋通讯作者：82450049＠qq.com Corresponding author：82450049＠qq.com