海浪谱的选择对海面电磁波散射建模的影响❋

王 珂，张 元，洪 峻，管爱红，杨 静，李红岩，明 峰

（1.河南工业大学信息科学与工程学院，郑州 450001；2.微波成像技术国家级重点实验室，北京 100190；3.中国科学院电子学研究所，北京 100190）

其中，可取n＝2。

由此，可建立PM谱，将其代入式（5）即建立Bragg共振散射模型。图5是u10＝5m/s时PM谱的半径部分随波数的变化，图6是PM谱的角度部分的变化，图7是u10＝5m/s时分别采用RA谱和PM谱的Bragg共振散射建模的比较，其中CMOD4模型［12］是ECMWF（欧洲中期天气预报中心）由大量实测数据获得的C频段、VV极化海面雷达后向散射的经验模型。通过与CMOD4模型数据（其可被看作是实测数据）的比较可见，选择不同海浪谱进行散射建模的结果有明显差异。相比之下，选择RA谱进行散射建模的结果更接近实测数据、效果更好。

海浪谱的选择对海面电磁波散射建模的影响❋

王 珂1，❋❋，张 元1，洪 峻2，3，管爱红1，杨 静1，李红岩1，明 峰2，3

（1.河南工业大学信息科学与工程学院，郑州 450001；2.微波成像技术国家级重点实验室，北京 100190；3.中国科学院电子学研究所，北京 100190）

海浪谱的选择对Bragg共振散射建模的影响是海面电磁波散射建模的关键问题。首先简介了海浪谱的概念，然后选择RA（Romeiser-Alpers）谱进行了Bragg共振散射建模，最后选择另一种具有代表性的PM（Pierson-Moskowitz）谱进行了Bragg共振散射建模，并通过仿真实验对两种海浪谱及其用于Bragg共振散射建模的效果进行了比较分析。获得的结论对合理地选择海浪谱具有指导意义。

雷达海洋遥感；海浪谱；海面；电磁波散射；建模影响

1 引言

雷达海洋遥感中，需要准确掌握电磁波的海面散射特性和散射模型，这样才能实现海洋现象的定量遥感。海面电磁波的散射机制，按照入射角范围，主要分为［1－2］镜面散射和Bragg共振散射。雷达入射角在20°～70°时，主要是Bragg共振散射机制产生了海面雷达后向散射。由于雷达观测角度多数情况下大于20°，例如ERS－2/SAR的入射角为23°［3］，ENVISAT/ASAR的入射角为15°～45°［4］，TerraSARX的入射角为20°～55°［5］，国内外学者广泛关注了海面Bragg共振散射的有关问题［1，6］。目前，国内外已对Bragg共振散射建模进行了一些研究［1，6－8］，普遍认为海浪谱是Bragg共振散射模型的重要组成部分，但有关海浪谱的选择对Bragg共振散射建模的影响及其比较分析的研究却少有论述。为了合理地选择海浪谱，进而能对Bragg共振散射准确建模，以满足雷达海洋遥感的需要，本文针对海浪谱的选择对海面电磁波散射建模影响的有关问题进行了深入研究，获得的结论对散射建模时海浪谱的选择具有指导意义。

2 海浪谱的概念

海浪可看作由无限个振幅不同、频率不同、方向不同、相位不同的波组成，具有明显的随机性［9］。海浪谱描述的是海浪的内部结构，通常用来说明海浪能量相对于其各组成部分（高频和低频）的分布。

定义海表面位移ζ的协方差为二维联合概率密度函数P（ζ1，ζ2）的二阶矩［9］，即：

式中，r、τ分别表示空间、时间间隔，x、t分别表示波浪的空间、时间位置。当其随机过程视为平稳时，协方差Z不随（x，t）变化，则Z（x，r；t，τ）可写为Z（r，τ）。

海浪谱与海表面位移的协方差是一对傅里叶（Fourier）变换，即：

式中，k、ω分别表示波浪的波数、频率。

海浪谱可理解为海浪方向谱，定义为二维海表面波高（位移）的协方差函数的Fourier变换，它表示了海浪各组成分量在频率和方向上的二维分布，也称波高谱。为了掌握海浪的统计特性，国外学者对海浪谱进行了深入研究，并通过长期观测和大量实验，提出了多种海浪谱表达形式［7－10］。常见的海浪谱主要有Pierson-Moskowitz谱、JONSWAP谱、Bretschneider谱、Wallops谱、Philips谱、Donelan-Banner-Jahne谱、Elfouhaily谱等。

3 海面电磁波散射模型

Bragg共振散射是海面电磁波散射建模的核心，是二尺度、多尺度等［1－2］复杂散射模型的基础。粗糙海面可看作是许多平面波的线性叠加，而电磁波散射也是线性过程，因此粗糙海面中各个不同波分量在远场（远离海面时）相干叠加，进而增强了具有特定尺度的周期性结构的散射，同时削弱了其他周期性结构的散射，其效应如同衍射光栅一样，这就是所谓的Bragg共振散射［1］，如图1所示。入射电磁波与特定波长的海面波发生Bragg共振，雷达接收散射回波信号，后向散射强度正比于海面Bragg波的谱密度。

图1 Bragg共振散射示意图Fig.1 Sketch of Bragg resonance scattering

能与入射电磁波发生共振的海面波称为Bragg波，其波长可由下式计算：

其中，λB为Bragg波长，λE为入射电磁波波长，θ为入射角。

根据海面电磁波散射扰动理论，可得到Bragg共振散射的归一化海面雷达后向散射截面的表达式

为［1，6］

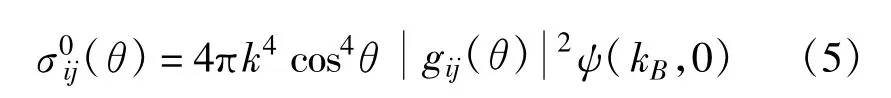
其中，ψ（·）是海浪方向谱，k为雷达波数，kB＝2k sinθ为Bragg波数，θ为雷达入射角，gij是Fresnel反射系数，与极化有关，下标i、j表示极化状态，分别为

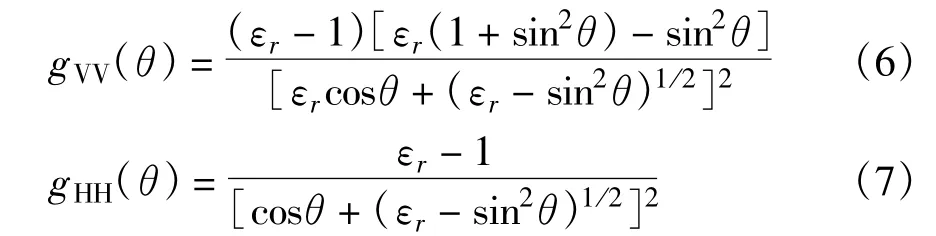
式中，εr为海水的相对介电常数。

通常，海浪方向谱ψ（k，φ）可写成半径部分和角度部分的乘积：

Apel［7］提出了Donelan-Banner-Jahne谱，在此基础上，Romeiser和Alpers［8］又提出了Romeiser-Alpers谱（简称RA谱），其表示为

式中，u10为海面以上10 m高度处的风速，φ为波向与风向的夹角。可见，半径部分和角度部分分别为

RA谱的各部分依次为

式中，PL是描述低波数滚降和以风速为自变量的JONSWAP峰值变化函数的因子，峰值波数kp与u10的关系为

其中，g为重力加速度。WH是用来模拟高波数区（即Bragg波数区）谱的形状，β是响应的风速指数，常数un＝1m/s用来修正ψ的量级。角度扩展函数S描述了谱的方向性，当φ＝0时，S（k，0，u10）＝1。经过3次最优化迭代过程，得到WH、β、S的表达式，分别为

综上所述，可建立RA谱和Bragg共振散射模型。图2是u10＝5 m/s时RA谱的半径部分随波数的变化，图3是RA谱的角度部分的变化，图4是u10＝5m/s时C频段Bragg共振散射的VV和HH极化随入射角的变化，可见VV极化总是大于HH极化，这是符合海面雷达后向散射实际情况的［1］。

图2 RA谱的半径部分随波数的变化Fig.2 Variety of radius part of RA spectrum with wave number

图3 RA谱的角度部分的变化Fig.3 Variety of angle part of RA spectrum

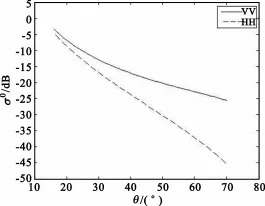
图4 C频段Bragg共振散射的VV和HH极化Fig.4 C band VV and HH polarization of Bragg resonance scattering

4 海浪谱的选择对散射建模的影响

前面提到过海浪谱有多种不同的表达，是由不同的学者各自独立提出的。那么，海浪谱的选择是否会对海面电磁波散射建模的结果产生影响，成为需要研究的问题。为此，我们选择另一种具有代表性的Pierson-Moskowitz谱［10］（简称PM谱）进行散射建模研究。

PM谱通常可写成半径部分和角度部分，Pierson和Moskowitz［10］、Holliday［11］将半径部分写为

其中，B＝0.001 435为力度参数，flr为低频率卷积部分，Pierson和Moskowitz定义其为

其中，kp为峰值波数，其与风速的关系为

其中，αp＝0.336为峰位置参数。

PM谱的角度部分，可采用如下形式：

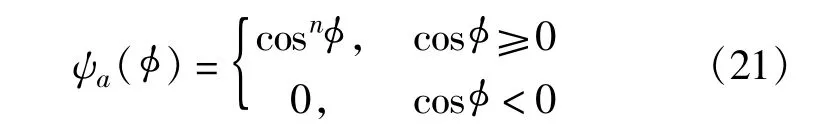
其中，可取n＝2。

由此，可建立PM谱，将其代入式（5）即建立Bragg共振散射模型。图5是u10＝5m/s时PM谱的半径部分随波数的变化，图6是PM谱的角度部分的变化，图7是u10＝5m/s时分别采用RA谱和PM谱的Bragg共振散射建模的比较，其中CMOD4模型［12］是ECMWF（欧洲中期天气预报中心）由大量实测数据获得的C频段、VV极化海面雷达后向散射的经验模型。通过与CMOD4模型数据（其可被看作是实测数据）的比较可见，选择不同海浪谱进行散射建模的结果有明显差异。相比之下，选择RA谱进行散射建模的结果更接近实测数据、效果更好。

图5 PM谱的半径部分随波数的变化Fig.5 Variety of radius part of PM spectrum with wave number

图6 PM谱的角度部分的变化Fig.6 Variety of angle part of PM spectrum

图7 两种谱的Bragg共振散射建模的比较Fig.7 Comparison of using two spectrums for Bragg resonance scatteringmodeling

图8是u10＝5m/s时RA谱与PM谱的半径部分的比较，可见两者在Bragg波数区（即kB附近）有明显差别，这势必会导致散射建模结果的差异。通过Bragg共振散射建模实验比较和海浪谱半径部分比较可见，并非任何海浪谱用于散射建模都能获得满意的效果，只有那些对Bragg波数区描述准确的海浪谱，在散射建模中才能取得与实测数据接近的结果。海浪谱可以通过理论研究、观测、实验等不同手段获得，各种海浪谱在某些方面也各有优缺点。而采用RA谱的散射建模效果之所以较好，是因为其在提出时使用散射计实测数据进行了充分匹配［8］。海浪谱的选择对散射建模结果有显著影响，对现有各种海浪谱用于散射建模的性能比较十分繁杂，将是以后的研究方向。

图8 RA谱与PM谱的半径部分的比较Fig.8 Comparison of radius partof RA spectrum and PM spectrum

5 结论

本文针对海浪谱的选择对海面电磁波散射建模影响的有关问题进行了研究，分别选择RA谱和PM谱进行了Bragg共振散射建模，并通过仿真实验对两种海浪谱及其用于Bragg共振散射建模的效果进行了比较分析。海浪谱的选择对散射建模结果有显著影响，选择不同海浪谱进行散射建模的结果有明显差异。只有选择那些对Bragg波数区描述准确的海浪谱，在散射建模中才能取得与实测数据接近的结果，而选择经过散射计实测数据充分匹配的海浪谱，往往可获得较好的散射建模效果。上述结论对散射建模时合理地选择海浪谱具有指导意义。

［1］Valenzuela GR.Theories of the interaction of electromagnetic and ocean waves－a review［J］.Boundary－Layer Meteorology，1978，13（1）：61－85.

［2］Plant W J.A stochastic，multiscale model of microwave backscatter from the ocean［J］.Journal of Geophysical Research，2002，107（C9）：3120－3140.

［3］European Space Agency.ERSoverview［EB/OL］.（2009－01－10）［2012－10－10］.http：//www.esa.int/esaEO/SEMGWH2VQUD－index－0－m.html.

［4］European Space Agency.ASAR product handbook［EB/OL］.（2009－02－10）［2012－11－10］.http：//envisat.esa.int/handbooks/asar/CNTR.html.

［5］German Aerospace Center.TerraSAR－X［EB/OL］.（2011－01－20）［2012－11－10］.http：//www.dlr.de/dlr/en/desktopdefault.aspx/tabid－10377/565－read－436/.

［6］Barrick D E.First order theory and analysis of MF/HF/UHF scatter from the sea［J］.IEEE Transactions on Antennas and Propagation，1972，20（1）：2－10.

［7］Apel JR.An improvedmodel of the ocean surface wave vector spectrum and its effectson radar backscatter［J］.Journal of Geophysical Research，1994，99（C8）：16269－16291.

［8］Romeiser R，AlpersW.An improved composite surfacemodel for the radar backscattering cross section of the ocean surface 1.Theory of the model and optimization/validation by scatterometer data［J］.JournalofGeophysical Research，1997，102（C11）：25238－25250.

［9］Phillips OM.The dynamics of the upper ocean［M］.2nd ed. England：Cambridge University Press，1977.

［10］Pierson W J，Moskowitz L.A proposed spectral form for fully developed wind seas based on the similarity theory of S.A. Kitaigorodskii［J］.Journal of Geophysical Research，1964，69（24）：5181－5190.

［11］Holliday D，St-Cyr G，Woods N E.A radar ocean imaging model for small to moderate incidence angles［J］.International Journal of Remote Sensing，1986，7（12）：1809－1834.

［12］Stoffelen A CM，Anderson D L T.Scatterometer data interpretation：derivation of the transfer function CMOD4［J］. Journal of Geophysical Research，1997，102（C3）：5767－5780.

王珂（1981—），男，河南郑州人，2011年于中国科学院电子学研究所获博士学位，现为讲师，主要研究方向为SAR遥感信息处理与应用；

WANG Ke was born in Zhengzhou，Henan Province，in 1981.He received the Ph.D.degree from Institute of Electronics，Chinese Academy of Sciences，in 2011.He is now a lecturer.His research concerns SAR remote sensing information processing and application.

Email：email－of－paper＠yahoo.com.cn

张元（1961—），男，河南洛阳人，1996年于南京理工大学获博士学位，现为教授，主要研究方向为智能信息处理与应用；

ZHANG Yuan was born in Luoyang，Henan Province，in 1961.He received the Ph.D.degree from Nanjing University of Science and Technology in 1996.He is now a professor.His research concerns intelligent information processing and application.

洪峻（1960—），男，安徽黄山人，1983年于中国科学技术大学获学士学位，现为研究员，主要研究方向为SAR遥感信息处理与应用；

HONG Jun was born in Huangshan，AnhuiProvince，in 1960. He received the B.S.degree from University of Science and Technology of China in 1983.He is now a senior engineer of professor. His research concerns SAR remote sensing information processing and application.

管爱红（1973—），女，河南商丘人，2006年于华中科技大学获博士学位，现为副教授，主要研究方向为信号与信息处理。

GUAN Ai-hong was born in Shangqiu，Henan Province，in 1973.She received the Ph.D.degree from Huazhong University of Science and Technology in 2006.She is now an associate professor. Her research concerns signal and information processing.

Influence of Choosing Ocean W ave Spectrum on Ocean Surface Electromagnetic W ave Scattering M odeling

WANG Ke1，ZHANGYuan1，HONGJun2，3，GUANAi-hong1，YANGJing1，LIHong-yan1，MINGFeng2，3
（1.School of Information Science and Engineering，Henan University of Technology，Zhengzhou 450001，China；2.National Key Laboratory ofMicrowave Imaging Technology，Beijing 100190，China；3.Institute of Electronics，Chinese Academy of Sciences，Beijing 100190，China）

The influence of choosing ocean wave spectrum on Bragg resonance scatteringmodeling is a key problem of ocean surface electromagneticwave scatteringmodeling.This paper studies thoroughly about related problems.It introduces the conceptofoceanwave spectrum，then chooses RA（Romeiser-Alpers）spectrum to perform Bragg resonance scatteringmodeling，finally chooses another representative PM（Pierson-Moskowitz）spectrum to perform Bragg resonance scatteringmodeling.By simulation experiment two ocean wave spectrums and their effect of application in Bragg resonance scatteringmodeling are compared and analyzed.Conclusions drawn in this paper have guidemeaning for choosing ocean wave spectrum reasonably.

radar ocean remote sensing；ocean wave spectrum；ocean surface；electromagnetic wave scattering；modeling influence

TN011

A

1001－893X（2013）04－0435－05

10.3969/j.issn.1001－893x.2013.04.012

2012－11－28；

2013－02－04 Received date：2012－11－28；Revised date：2013－02－04

国家自然科学基金资助项目（61071197）；河南工业大学高层次人才基金项目（2011BS044）

Foundation Item：The National Natural Science Foundation of China（No.61071197）；High Layer Talented Person Foundation of Henan University of Technology（2011BS044）

❋❋通讯作者：email－of－paper＠yahoo.com.cn Corresponding author：email－of－paper＠yahoo.com.cn