过模波导器件的迭代设计方法

王 强 周海京 杨 春 李 彪何晓阳

1)(中国工程物理研究院，电子工程研究所，绵阳 621900)

2)(应用物理与计算数学研究所，北京 100094)

3)(清华大学，工程物理系，北京 100084)

(2012年12月8日收到;2013年2月25日收到修改稿)

1 引言

随着高功率微波应用越来越广泛，过模波导器件的应用也越来越频繁[1].从模式保留和转换的角度，过模波导器件可分为三类：模式转换器，实现一个波导模式向另外一个波导模式的转换，例如TM01—TE11模式转换器;模式保留器，器件输入端和输出端模式相同，但器件结构特性(半径变化或者轴线弯曲)发生改变，例如TE01模式过渡器、TM01弯头结构;模式综合器，输入为一个模式，输出为模式分布，例如光壁馈源喇叭.这些过模波导常常可采用耦合波理论进行描述.在高功率微波的不同应用需求中，涌现了大量以耦合波理论为基础的设计方法：相位重匹配法[2]、常曲率法[3]、基于结构参数的蜂窝优化方法[4]、Dolph-Chebyshev方法[5]，等等.然而，这些传统设计方法都只解决某一种器件的设计或者对某种器件的某个指标进行改进[6].最近几年出现了迭代设计法，该方法能够对三类过模波导统一设计，设计结构相比于传统方法能够具备更优的电特性和结构特性，甚至能设计传统方法无能为力的新型器件.迭代法存在两条发展路线：基于整体结构轮廓优化和基于耦合波理论的优化求解.第一条路线由Denisov等完成[7,8]，但他们在公开发表的文献中对于具体技术细节披露甚少.第二条路线由Eric等提出[9]，他们完成了迭代梯度的求解工作，但没有给出迭代步长的合理取值方法并且对具体应用描述较少.本文在Eric的工作的基础上，完成了迭代步长求解，建立了通用迭代法设计流程.在设计实例部分，设计了双频TM01—TE11模式转换器和光壁馈源喇叭.双频TM01—TE11模式转换器的设计未见报道，本文首次报道了此类器件的设计和仿真结果;光壁馈源喇叭虽然设计方法较多，但以耦合波理论为基础进行设计也尚属首次.

2 迭代法原理

耦合波理论[10]对非均匀波导进行描述时，认为：当遭遇波导不均匀性(轴线弯曲、半径渐变或边界阻抗改变)时，不同模式间将发生模式耦合.忽略反射模和波导损耗的耦合波方程组如式(1)：

A为模式复幅度向量，z为轴线坐标，j为虚数单位，β为模式传播常数，s为结构函数，结构函数的选择与耦合机理有关系，对于轴线弯曲波导s为曲率，而对于半径渐变波导s为 d(lna)/dz，a为半径，C为耦合系数矩阵.模式沿轴的变化可分为两部分，一部分为自身相位的变化，第二部分为其他模式对该模式的耦合项.

过模波导器件设计问题可描述为：已知输入模式分布和输出模式分布，如何设计器件结构，使得最终效率最高.将结构作为待优化的函数，将效率作为优化目标，这个问题为泛函优化问题

s(z)为结构函数，J(s)为效率.将结构函数离散化为N个结构变量，S=(s1,s2,...,sN)，则泛函优化问题转换为多变量优化问题.在数学上，多变量优化问题常常采用最速下降法进行求解，求解过程为如下迭代过程：给定初始结构;对第p次迭代，判断结构性能是否达到要求，如果满足则迭代过程结束，如果不满足，采用Sp+1=Sp+tpΔSp更新结构，并进行第p+1次迭代.其中，S为结构向量，tp为第p步迭代步长，ΔSp为梯度，也即J(S)关于每一个结构变量的偏导数.迭代法的两个关键步骤为：梯度求解和迭代步长求解.梯度为器件改善的方向，而迭代步长决定了沿着这个方向走多远，两者的正确计算决定了迭代过程能否快速有效收敛.

2.1 梯度求解

梯度求解过程需要求出效率J(S)对每一个变量sk的偏导数.求解过程如下[9]：记Wk为模式分布函数A对sk的偏导数，为便于与直波导连接，要求Wk(0)=0.(1)式对sk求导，

其中，Rm为目标模式分布.可得到效率J(S)随sk的偏导：

2.2 迭代步长

为计算迭代步长，需将梯度表达式(9)重新写为多条耦合线叠加的形式：

在每步迭代中，总能够找到贡献最大的耦合线，与其他耦合线相比，改变这条耦合线的幅度更能够提高效率，因而可针对这条耦合线来计算迭代步长.在两模耦合过程中，下式形式的耦合系数分布能够有效实现模式变换：

2.3 迭代法设计流程

迭代过程只针对结构函数进行设计，对于轴线弯曲耦合机理，结构函数为曲率，对于半径渐变耦合机理，结构函数为半径对数相对于传播变量的导数.可在每次迭代过程中，添加结构控制方法，稍微改变结构函数，从而实现某些特殊的结构特性，例如，共轴、结构弯曲一定角度、或者输入输出半径控制，等等.以结构90°弯曲为例，控制方法为

其中，ρnew为结构控制之后的曲率函数，ρold为结构控制之前的曲率函数，L为结构总长度.给出较好的初始结构之后，每次迭代时结构控制方法对结构函数改变很少，并不会影响迭代进程.最终迭代法设计流程如图1所示.

3 设计实例

对于常规的模式变换器，本文作者已经做了相关研究，并与传统方法进行了比较，包括：宽带紧凑型TE01—TE11模式变换器[11]和一周期TE02—TE01模式变换器[12]，从比较结果中看出：迭代法设计的器件不仅带宽更宽，而且结构也能更紧凑.这儿给出两个设计实例，采用传统方法较难实现.

3.1 双频TM01-TE11模式变换器

双频高功率微波源[13]是目前研究方向之一，然而双频模式变换器却鲜见报道，采用迭代法可设计双频工作的模式变换器.双频模式变换器的设计需要在基本迭代法的基础上稍作修改：基本迭代法的梯度求解是在一个频点下计算得到，而双频器件的梯度求解需要在两个频点下分别计算，然后加权求和，求和结果作为新的梯度，再代入迭代法进行计算.根据新的梯度方向来改变结构能够提高这两个频点处的转换效率.设计了工作频点为8.75 GHz和10.3 GHz的双频TM01—TE11模式变换器，波导半径为16 mm.结构总长度为793 mm，如图2所示.采用CST建模仿真，带宽曲线如图3所示，从图中看出存在两个模式转换频带：频带1的中心频点为8.75 GHz，转换效率为99.93%，带宽达到0.22 GHz;频带2的中心频点为10.3 GHz，转换效率为99.86%，带宽达到0.48 GHz.8.75 GHz和10.3 GHz的模式耦合过程分别如图4(a)，(b)所示.

图1 过模波导器件的迭代法设计流程

图2 双频TM01—TE11模式变换器示意

图3 双频TM01—TE11模式变换器带宽曲线

图4 不同频率下模式耦合过程 (a)8.75 GHz;(b)10.3 GHz

3.2 光壁馈源喇叭设计

在高功率微波系统中，光壁喇叭相比于波纹喇叭能够降低打火风险.采用迭代法能够快速设计光壁喇叭.光壁喇叭需要完成TE11模式向基模高斯束的转换.选择高斯束束腰半径为w=0.6a，将高斯束的场分布按照波导模式作展开，得到波导模式成分为：TE11成分80.4%，TM11成分18%，与TE11相位相差π，TE12成分为1.6%，与TE11同相.光壁喇叭的设计为模式综合问题，可采用迭代法快速设计.设计了工作频率为35 GHz的光壁喇叭，输入半径为16 mm，输出半径为40 mm.结构总长度为426 mm，结构如图5所示.在PC机上的总计算时间为2 min.采用CST建模仿真，方向图计算结果如图6所示，从图中看出方向图的E面、45°切面和H面重合度达到25 dB，高斯束成分较高，达到了光壁喇叭的设计要求.

图5 光壁馈源喇叭示意

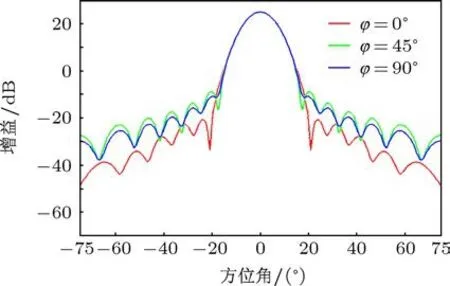
图6 光壁喇叭的CST仿真远场方向图

4 结论

本文介绍了过模波导器件的迭代设计方法，该方法能够快速自动完成模式变换器、渐变器和模式综合器件的设计，通过添加结构控制方法，还能够实现指标改进.采用迭代法设计了双频TM01—TE11模式转换器和光壁馈源喇叭两个过模波导器件.双频TM01—TE11模式转换器的两个工作频率分别为8.75 GHz和10.3 GHz，波导半径为16 mm，CST仿真结果表明两个频点处的转换效率分别为99.93%和99.86%，达到预期指标.光壁馈源喇叭工作频率为35 GHz，输入半径为16 mm，输出半径为40 mm，CST仿真结果表明远场方向图的E面、H面和45°切面有25 dB的重合度，高斯束成分较高.迭代法为过模波导器件设计的通用方法，为了适应不同的工程需求，可在基本迭代法的基础上作多种改进.针对不同需求的改进方法的研究仍然是一个很值得研究的方向.

[1]Thumm M K，Kasparek W 2002 IEEE Trans.on Plasma Sci.30 3

[2]Kumric H，Thumm M K，Wilhelm R 1988 INT.J.Electron.64 1

[3]Vinogradov D V，Denisov G G 1991 Int.J.Infrared Millim.Waves 12

[4]Yang S W，Qing A Y 2005 IEEE Trans.on Plasma Sci.33 4

[5]FlugelH，Kuhn E 1988 IEEE Trans.on Microwave Theory Tech.36 2

[6]Sun X，ZhaoQ，LiH F 2008 Acta Phys.Sin.57 4(in Chinese)[孙旭，赵青，李宏福2008物理学报57 4]

[7]Denisov G G，Kalynova G I，Sobolev D I2004Radiophysics and Quantum Electronics 47 8

[8]Sobolev D I，Denisov G G 2010 IEEE Trans.on Plasma Sci.38 10

[9]Luneville E，Krieg J M 1998 IEEE Trans.on Microwave Theory Tech.46 1

[10]Sporleder F，Unger H G 1979 Waveguide Tapers Transitions and Couplers(London：Peregrinus on behalf of the Institution of ElectricalEngineers)p30

[11]Wang Q，Zhou H J，Yang C，LiB，Ye J 2013 High power Lasers and Particle Beams 25 3(in Chinese)[王强，周海京，杨春，李彪，叶建2013强激光与粒子束25 3]

[12]Wang Q，Zhou H J，Yang C，LiB 2013 High power Lasers and Particle Beams 25 2(in Chinese)[王强，周海京，杨春，李彪2013强激光与粒子束25 2]

[13]Fan Y W，Zhong H H，LiZ Q，Shu T，Zhang J D，Zhang J，Zhang X P，Yang J H，LuoL 2007 J.Appl.Phys.102 103304