AlC分子X4Σ-和B4Σ-电子态的光谱性质*

刘 慧 邢 伟 施德恒 孙金锋 朱遵略

1)(信阳师范学院物理电子工程学院，信阳 464000)

2)(河南师范大学物理与信息工程学院，新乡 453007)

(2012年12月6日收到;2013年1月31日收到修改稿)

1 引言

随着量化理论和计算技术的进步，人们已能对金属及其碳化物的光谱性质开展研究，大大提高了我们对金属团簇的了解.元素Al和C在太空中含量丰富，由它们构成的双原子分子AlC可能存在于恒星大气或星际空间中[1].深入了解AlC分子的光谱信息，将有助于确定宇宙中AlC分子的含量与分布，帮助我们了解宇宙的起源与演化.AlC分子的光谱性质已引起了一些光谱学家的关注[2-8].

实验方面，早在1990年，Knight等[2]观测了AlC分子的电子自旋响应光谱.确定了AlC分子的自旋分裂和精细结构常数，标定了该分子基态对称性为4Σ-.1993年，Thoma等[3]在固态氩中采用傅里叶变换荧光光谱分析方法，探测到AlC分子.同年，Brazier[4]利用发射光谱对气相AlC分子的光谱性质进行了研究，获得了X4Σ-和B4Σ-态的某些光谱常数及分子常数.

理论方面，率先对AlC分子开展研究的是Zaitsevskii等[5].1986年，Zaitsevskii等[5]用多参考组态相互作用方法结合有效核势近似，使用价DZ+P STO基组，研究了BC和AlC分子的电子结构.他们计算了 AlC 分子 X4Σ-，2Π，2Δ 和2Σ-等电子态的势能曲线、偶极矩函数及相应的光谱常数.1988年，Bauschlicher等[6]采用MRCI理论方法计算了AlC分子大量低电子态的势能曲线，得到了Te，Re和ωe等光谱常数.计算中Al和C原子分别使用的基组为：(20s13p6d4f)/[5s4p2d1f]和 (13s8p6d4f)/[4s3p2d1f]ANO.1999年，Gutsev等[7]采用耦合簇CCSD(T)理论结合[14s9p4d3f/7s7p43f]/C和[17s12p5d4f/7s7p5d4f]/Al的原子轨道基，计算了AlC分子基态及两个低激发态的Re，Be和ωe等光谱数据.2001年，Tzeli等[8]采用CASSCF，MRCI及MRCI+Q等理论方法结合相关一致基aug-cc-pVQZ计算了AlC分子31个电子态的势能曲线.获得了这些电子态的 Te，Re，ωe，ωexe和αe等光谱常数.

分析已有的文献[2—8]发现，大多数理论研究集中在AlC分子的光谱常数上，对于分子的振动能级Gυ、惯性转动常数Bυ等分子常数则未见报道.且已有的理论计算均未考虑核价相关及相对论效应对分子能量及光谱性质的影响，使得理论结果与实验结果之间还有较大偏差.为了深刻理解AlC分子的性质，我们对该分子X4Σ-和B4Σ-态的光谱性质进行了研究.

本文采用Davidson修正[9,10]的内收缩多参考组态相互作用[11,12]方法(MRCI+Q)及Dunning等[13-17]的相关一致基 aug-cc-pVnZ(n=D，T，Q，5，6)于 0.16—1.65 nm 的核间距范围内计算了AlC分子X4Σ-和B4Σ-态的势能曲线.对势能曲线进行了相对论修正及核价相关修正计算，同时利用总能量外推进行基组截断误差修正.通过求解核运动的径向Schrdinger方程，获得了无转动AlC分子两个电子态的全部振动态.通过对前16个振动能级的拟合，得到了这两个电子态的光谱常数.另外，本文还进一步计算了与每一振动态相对应的惯性转动常数等分子常数.

2 理论方法

本文中，AlC(X4Σ-，B4Σ-)分子的势能曲线是在MOLPRO2010.1程序包[18]中计算的.我们选择能够准确描述分子相关能的MRCI方法来研究AlC分子的光谱性质.CASSCF计算为随后的MRCI及MRCI+Q计算提供参考波函数.

MOLPRO只能使用Abelian点群.对于具有简并对称性的分子，如对称性为C∞v的AlC分子，计算中必须用C2v群替代.C2v群对应的不可约表示是a1/b1/b2/a2.这4种类型的轨道参与计算.具体地，在计算中将8个分子轨道放入活化空间，这包括4个a1、2个b1及2个b2轨道.其中，把Al原子的3s3p壳层和C原子的2s2p壳层的电子放入活性轨道，构成价态空间.也就是说，AlC分子最外层的7个电子分布于8个轨道中.因此，活性空间表示为(7，8).其余的电子则放入6个闭壳层轨道中，分别是4个a1、1个b1和1个b2轨道.这样，实际参与计算的分子轨道共14个，分别为8a1/3b1/3b2.

势能曲线的计算使用的基组是Dunning等的相关一致基，aug-cc-pVnZ(n=D,T,Q,5,6).计算在0.16—-1.65 nm核间距范围内进行.步长一般取为0.05 nm，只是在平衡位置附近，为充分展示势能曲线的性质，计算步长才取为0.02 nm.

即使是AlC这样的小分子，核价相关效应及相对论效应对分子能量的影响也是不能忽略的.为评价核价相关效应及相对论效应对分子能量及光谱常数的影响，本文针对X4Σ-和B4Σ-这两个电子态，于MRCI/aug-cc-pV6Z(AV6Z)和MRCI+Q/AV6Z理论水平计算了分别包含核价相关修正、相对论修正及同时包含两种修正的势能曲线.这里，我们利用三阶Douglas-KrollHamilton近似[19,20]结合cc-pV5Z-DK相对论收缩基进行相对论能量修正计算(记为DK).由核价相关及相应的冻结核近似的能量差作为核价相关修正结果(记为CV).计算使用的基组是aug-cc-pCVTZ.需要说明的是，核价相关效应计算中Al原子2s2p3s闭壳层和C原子1s2s闭壳层的14个电子参与运算，Al原子1s层电子被冻结.与价态范围内的计算相同，两种修正计算也是在0.16—1.65 nm核间距范围内进行的.除平衡位置附近计算步长取为0.02 nm外，其余的计算步长均取为0.05 nm.

为了弥补基组截断误差，本文将相关能外推公式扩展到总能量外推[21]，

其中，ΔEtotal,∞是外推至完全基组极限的总能量.ΔEtotal,X和 ΔEtotal,X+1分别是由 aug-cc-pVXZ和aug-cc-pV(X+1)Z基组计算的总能量.这里，我们使用aug-cc-pV5Z(表示为AV5Z)和AV6Z基组计算的势能值结合(1)式进行总能量外推，得到外推的势能曲线(表示为56).将外推的分子总能量加上相对论修正及核价相关修正结果，得到了同时考虑两种修正的外推势能曲线(记为56+CV+DK).

3 结果与讨论

3.1 基组的收敛行为

首先来讨论基组的收敛行为.使用MRCI和MRCI+Q理论方法不同的基组[AVnZ(n=D,T,Q,5,6)]计算出的势能曲线，求解径向振转Schrdinger方程、并通过进一步的数据拟合，获得了 Te，Re，ωe，ωexe，ωeye，Be和αe等光谱常数.限于篇幅，仅以 X4Σ-态的 Re，ωe和ωexe及 B4Σ-态的Te，Re和ωe为例进行讨论.为便于比较，将外推结果与最近的实验结果[4]一并列入表1中.

从表1可以看出，对于X4Σ-态，无论是MRCI还是MRCI+Q方法，随着基组由aug-cc-pVDZ增大到AV6Z，Re，ωe及ωexe均向完全基组极限处收敛.其中，Re值逐渐缩短，ωe逐渐增大.与实验结果[4]相比，随着基组增大，Re和ωe向实验结果靠拢.当外推至完全基组极限时，Re和ωe与实验结果最接近.

对于B4Σ-态，在MRCI和MRCI+Q理论水平，随着基组增大，Te，Re及ωe值均向完全基组极限收敛.可以看出，Re及ωe值随基组变化的趋势与X4Σ-态相同.其中，Re值逐渐缩短，ωe逐渐增大.与实验结果[4]相比，随着基组增大，ωe值逐渐向其靠拢.使用AV6Z基组计算的ωe值与实验值仍有4.42 cm-1(MRCI)和6.54 cm-1(MRCI+Q)的偏离.当外推至完全基组极限时，与AV6Z计算的结果相比，ωe相对于实验值的误差分别减小了1.54 cm-1(MRCI)和1.64 cm-1(MRCI+Q)，使得ωe的计算精度显著改善.容易看出，Te随基组增大不断降低.且随着基组增大，Te明显偏离实验结果.分析表明，其原因在于核价相关效应和相对论效应对分子总能量产生或多或少的影响，特别是核价相关效应对小分子的总能量有较大影响.而上述计算均是在价态范围内进行的，未考虑两种效应对分子能量的影响，这应该是导致Te明显偏离实验值的原因.

表1 MRCI和MRCI+Q理论方法下基组对X4Σ-态的Re，ωe及ωexe和B4Σ-态的Te，Re及ωe的影响

根据上述分析发现，经过总能量外推的势能曲线拟合出的Re和ωe接近实验值.可见，计算中使用大基组外推至完全基组极限可以明显改善分子的Re和ωe，使分子光谱的预测更加准确.

3.2 核价相关及相对论修正对分子能量的影响

这里，以B4Σ-态为例，分析核价相关修正、相对论修正及Davidson修正对分子能量的影响.在平衡位置附近，核价相关修正使分子的总能量降低约0.00155(MRCI)/0.00262(MRCI+Q)Hartree(1 Hartree=27.21 eV).相对论修正给分子的总能量带来约0.00068(MRCI)/0.00068(MRCI+Q)Hartree的降低.Davidson修正也使分子的能量发生一定的变化，使平衡位置的能量降低约0.00038 Hartree.可见，核价相关、相对论修正及Davidson修正对总能量产生了不同程度的影响.其中，核价相关修正的影响最大.

对MRCI/AV6Z及MRCI+Q/AV6Z理论水平下的势能曲线进行相对论修正或/和核价相关修正.拟合这些势能曲线，计算得到了各种修正下的光谱常数.将同时考虑相对论修正和核价相关修正的外推势能曲线拟合，也获得了包含两种修正的外推光谱常数.限于篇幅，表2只列出了B4Σ-态的光谱常数Te，Re及ωe的CV，DK及CV+DK的修正量.为便于比较，实验结果[4]也列入该表中.

表2 各种修正对B4Σ-态的光谱常数Te，Re及ωe的影响

与实验结果[4]比较发现，无论是采用MRCI方法还是MRCI+Q方法，核价相关修正使Re缩短0.00075 nm，使ωe增加约10 cm-1.考虑核价相关修正使Te的计算质量显著提高.使Te分别升高341.06 cm-1/MRCI和574.36 cm-1/MRCI+Q.这些变化使Re，ωe和Te均向实验结果靠拢.相对论修正对Re的影响很小，两种理论方法下，仅使Re缩短约0.00002 nm.与核价相关修正产生的趋势相反，相对论修正使ωe值分别减小1.56 cm-1(MRCI)和1.62 cm-1(MRCI+Q).两种理论方法下，相对论修正均使Te增大149.68 cm-1.由表1可以清楚的看到，同时加入核价相关和相对论修正后，Re，ωe和Te均趋近于实验结果.核价相关修正及相对论修正明显改善了B4Σ-态光谱质量.

同时加入核价相关和相对论修正后，经总能量外推的ωe和Te与实验值[4]符合很好.例如，MRCI+Q理论计算得到的ωe和Te偏离实验值[4]分别只有0.49%和0.95%.根据误差范围分析方法[22,23]可以推断，高于四重激发的能量校正很小，不超过74.30 cm-1，约占激发能的0.33%.

3.3 势能曲线

根据上述讨论及分析可以得出结论：使用大基组计算并将分子总能量外推至完全基组极限，同时考虑各种修正对分子能量的影响将有助于准确预测分子的势能曲线及光谱性质.图1展示了在MRCI+Q/56+DK+CV理论水平下获得的X4Σ-和B4Σ-的势能曲线.

图1 MRCI+Q/56+CV+DK理论水平下的势能曲线(1为X4Σ-：2 为 B4Σ-)

图1显示，X4Σ-和B4Σ-电子态的势能曲线均光滑且收敛.基态有很深的势阱，是一个稳定态;B4Σ-态是一个亚稳态，其势能曲线分别存在一个势阱和一个势垒.势垒大约位于0.2240 nm处，高约1215.89 cm-1(0.00554 Eh).

3.4 光谱常数

利用3.3中MRCI+Q/56+CV+DK理论水平下X4Σ-和B4Σ-态的势能曲线，计算得到了这两个态的光谱常数 Te，Re，ωe，ωexe，ωeye，Be和 αe.为便于比较，我们将这些数据和已有的实验结果[4]及其他理论结果[5-8]一起列入表3中.

从表3可以清楚地看到，迄今为止只有4篇文献[5—8]计算了X4Σ-态的光谱性质.具体地，Zaitsevskii等[5]用多参考组态相互作用方法结合有效核势近似，计算了AlC分子基态的ωe和ωexe.其ωe和ωexe值与实验值[4]分别相差25.84 cm-1(3.95%)和1.9067 cm-1(44.41%)，与实验结果偏离较大.Bauschlicher等[6]采用CASSCF及MRCI理论方法并使用原子轨道基计算了该分子基态的Re和ωe.表3列出了在MRCI理论方法下得到的结果.其Re比实验值长0.00231 nm(1.18%).ωe值与实验值相差25.84 cm-1(3.95%).这些结果偏离实验结果较大.Tzeli等[8]采用CASSCF，MRCI及MRCI+Q理论方法和aug-cc-pVQZ基组在价态范围内计算了该分子基态的光谱常数.在MRCI方法下的结果见表3.由表3可以看出，其Re，ωe，ωexe和αe值与实验值分别偏离0.82%，0.62%，1.71%和12.69%.Gutsev等[7]采用CCSD(T)方法和原子轨道基计算了该分子基态的Re，Be和ωe等光谱常数.它们与实验结果符合较好，与本文的计算精度相当.然而，遗憾地是，他们的计算只涉及了有限的几个光谱数据.

表3 AlC分子X4Σ-和B4Σ-电子态的光谱常数与实验结果和其他理论计算的比较

对B4Σ-态，有3个研究小组[5,6,8]报道了其计算结果，这些结果均已列于表3中.由表3可知，Bauschlicher等[6]采用MRCI方法计算的Re和ωe分别偏离实验值[4]1.94%和2.85%，只有Te和实验值符合较好，偏离仅为0.72%.Zaitsevskii等[5]只计算了该态的激发能，且与实验值相差4273.79 cm-1(19.06%)，偏离较远.Tzeli等[8]的最好结果是在MRCI理论计算中获得的，其Te，Re，ωe和ωexe值偏离实验结果分别为1.59%，0.99%，1.76%和4.71%.

简单的计算可知，本文在MRCI+Q/56+DK+CV理论水平下计算的光谱常数与实验结果[4]符合较好.对于 X4Σ-态，本文的 Re，ωe，ωexe和 Be值与实验值的偏离分别仅为0.08%，0.73%，0.13%和0.04%.对于 B4Σ-态，Te，Re，ωe，ωexe和 Be与实验值的偏离分别仅为0.95%，0.09%，0.49%，0.26%和0.21%.只有小量αe与实验值的偏离稍大.

通过上面的讨论可知，本文在MRCI+Q/56+CV+DK理论水平下获得的光谱数据整体上与实验结果符合较好，优于已有的理论结果.可以确定，本文在MRCI+Q/56+CV+DK理论水平下得到的势能曲线是准确、可靠的.

本文的计算结果之所以准确，其原因有多个方面.其一，本文在采用高精度的内收缩多参考方法的基础上引入了核价相关修正及相对论修正，而其他的理论研究却未将这些重要的影响因素包含在内.特别是，核价相关修正及相对论修正明显改善了B4Σ-态的激发能.可见，即使是AlC这样的小分子，要准确预测其光谱信息，核价相关效应及相对论效应的影响也必须考虑在内.其二，计算使用的总能量外推方法减小了由于基组截断导致的残余误差.使得Re和ωe更加准确.再者，采用的Davidson修正也进一步减小了理论结果与实验结果之间的偏离.

3.5 振动能级及惯性转动常数

利用MRCI+Q/56+CV+DK理论水平得到的势能曲线，通过求解核运动的径向Schrdinger方程，找到了无转动的X4Σ-和B4Σ-态的全部振动态，计算了与每一振动态相对应的振动能级和惯性转动常数.只有前4个振动能级有实验结果[4].这里，仅在表4中列出前10个振动态的计算结果.

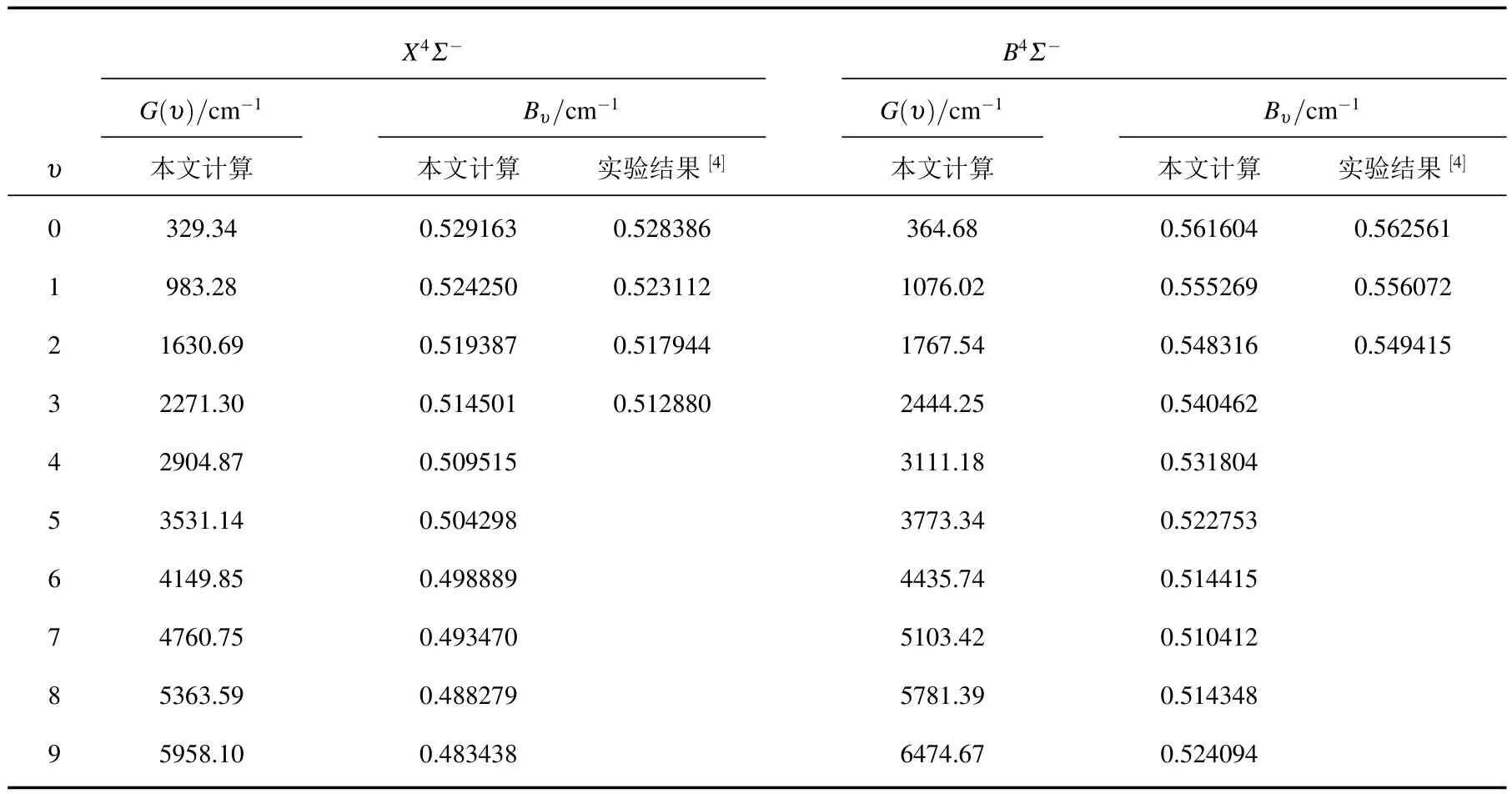
表4 AlC分子X4Σ-和B4Σ-电子态的分子常数与已有的实验结果的比较

只有一篇文献[4]报道了AlC分子X4Σ-和B4Σ-态的Bυ实验值.为便于比较，我们将这些结果也列入表4中.从表中容易看出，本文计算获得两个电子态的Bυ与实验结果符合很好.υ=0—3时，X4Σ-电子态的Bυ值与实验值的相对误差分别为0.15%，0.22%，0.28%和0.32%.B4Σ-态的Bυ值与实验值的相对误差分别为0.17%(υ=0)，0.14%(υ=1)和0.20%(υ=2).这些结果都是相当好的.

由于尚未找到AlC分子X4Σ-和B4Σ-态的振动能级和较高振动态的惯性转动常数的实验或理论结果，因而无法将本文得到的数据直接与其进行比较.但是，根据前文中关于这两个电子态的光谱常数与实验结果及其他理论计算的比较以及两个电子态的分子常数与现有实验结果的比较可以断定，在MRCI+Q/56+CV+DK理论水平下得到的势能曲线是准确的.尽管没有更多的实验数据供本文比较，我们依然有理由相信，AlC分子这两个电子态的振动能级和较高振动态的惯性转动常数的预测是可靠的.

随着现代通信及微波毫米波技术的飞速发展，通信系统及射频微波模块逐渐向低成本、小型化，高性能的趋势发展，这也是未来通信行业里极具竞争力的产品的特点。低温共烧陶瓷(LTCC)技术由于成熟的发展理论，稳定的电气性能和相对低廉的生产成本成为目前电子元器件小型化发展较为迅速的一个领域 [1-2]。LTCC是一种多层基板结构，它是以陶瓷材料作为介质基板，金、银、铜等导电性能良好的金属作为导电材料，将无源元件埋置于基板中，在800℃～900℃温度下把陶瓷介质基板和导电金属材料一同烧结成一种具有高性能、小型化的电子元件和电路组件。

4 结论

本文采用Davidson修正的MRCI方法及Dunning等的相关一致基于0.16—1.65 nm的核间距范围内计算了AlC分子X4Σ-和B4Σ-态的势能曲线.利用总能量外推公式对势能曲线进行了外推.对分子能量进行了相对论修正及核价相关效应修正，获得了同时考虑两种效应修正的外推势能曲线.拟合势能曲线，得到了这两个态的光谱常数Te，Re，ωe，ωexe，ωeye，Be和αe.详细讨论了基组及核价相关和相对论修正等对其能量和光谱常数的影响.在MRCI+Q/56+CV+DK理论水平下得到的光谱常数与已有的实验结果符合较好.通过求解核运动的径向Schrdinger方程，找到了AlC(X4Σ-，B4Σ-)分子的全部振动态.针对每一振动态，还分别计算了与其对应的振动能级和惯性转动常数等分子常数.这些数据均与已有的实验值一致.文中AlC(X4Σ-，B4Σ-)分子的振动能级和较高振动态的惯性转动常数属首次报道.本文的理论研究方法可以为同类研究提供有益的借鉴.本文的计算结果可为进一步的实验研究提供参考.

[1]TsujiT 1973 Astron.Astrophys.23 411

[2]Knight L B，CobranchiS T，Herlong J O，Arrington C A 1990 J.Chem.Phys.92 5856

[3]Thoma A，Caspary N，WurfelB E，Bondybey V E 1993 J.Chem.Phys.98 8458

[4]Brazier C R 1993 J.Chem.Phys.98 2790

[5]ZaitsevskiiA V，Dement’ev A I，Zviadadze G N 1986 J.Less.Common Met.117 237

[6]Bauschlicher C W，Langhoff S R，Pettersson L G M 1988 J.Chem.Phys.89 5747

[7]Gutsev G L，Jena P，Bartlett R J 1999 J.Chem.Phys.110 2928

[9]Langhoff S R，Davidson E R 1974 Int.J.Quantum Chem.8 61

[10]Richartz A，Buenker R J，Peyerimhoff S D 1978 Chem.Phys.28 305

[11]Werner H-J，Knowles P J 1988 J.Chem.Phys.89 5803

[12]Knowles P J，Werner H J 1988 Chem.Phys.Lett.145 514

[13]Dunning T H 1989 J.Chem.Phys.90 1007

[14]Woon D E，Dunning T H 1993 J.Chem.Phys.98 1358

[15]Van Mourik T，Wilson A K，Dunning T H 1999 Mol.Phys.96 529

[16]Van Mourik T，Dunning T H 2000 Int.J.Quantum Chem.76 205

[17]De Jong W A，Harrison R J，Dixon D A 2001 J.Chem.Phys.114 48

[18]Werner H J，Knowles P J，Lindh R，Manby F R，Schtz M，CelaniP，Korona T，Mitrushenkov A，Rauhut G，Adler T B，Amos R D，Bernhardsson A，Berning A，Cooper D L，Deegan M J O，Dobbyn A J，Eckert F，GollE，HampelC，Hetzer G，Hrenar T，Knizia G，KpplC，Liu Y，Lloyd A W，Mata R A，May A J，McNicholas S J，Meyer W，Mura M E，Nicklass A，PalmieriP，P flger K，Pitzer R，Reiher M，Schumann U，StollH，Stone A J，TarroniR，Thorsteinsson T，Wang M，Wolf A MOLPRO(a package of ab initioprograms)(version 2008.1)http：//www.molpro.net

[19]Reiher M，Wolf A 2004 J.Chem.Phys.121 2037

[20]Wolf A，Reiher M，Hess B A 2002 J.Chem.Phys.117 9215

[21]Liu H，Xing W，ShiD H，Sun J F，Zhu Z L 2012 Acta Phys.Sin.61 203101(in Chinese)[刘慧，邢伟，施德恒，孙金峰，朱遵略2012物理学报61 203101]

[22]Bauschlicher C W，Partridge H 1996 Chem.Phys.Lett.257 601

[23]Karton A，Martin J M L 2006 J.Chem.Phys.125 144313