收入方程优化及估算方法研究

王云多

(黑龙江大学 经济与工商管理学院，黑龙江 哈尔滨150080)

一、引 言

近年来，国内外一些学者使用一些参数化或非参数化方法考察收入方程优化问题和估算人力资本收益率。例如，Heckman and Polachek率先从实证角度考察了收入方程中收入和教育水平之间的函数形式，认为二者之间存在非线性关系，而Horowitz指出半参数法是使用因变量未特指收入方程估算人力资本收益率的最佳方法，Chen等进一步研究参数化收入方程，考察秩估计在收入方程中的应用，Klein and Sherman认为半参数法是考察收入方程的最佳方法，Abrevaya and.Hausman综合上述学者的研究思想，考察了参数化博克斯考克斯收入方程和非参数收入方程的应用条件。近年来，我国学者开始关注参数化收入方程，如王明进、岳昌君运用半参数方法，研究了工龄对教育收益率的影响。赵西亮、朱喜使用Probit模型，运用倾向指数匹配方法研究了家庭背景及地区对个人上大学的概率和教育收益率的影响。

上述学者在实证研究中所用的数据多为由政府的专业调查机构提供，数据可靠可直接用于收入方程估计。可是，收入方程经验研究中，问卷调查数据难以满足这一要求，由于问卷调查面临调查对象不合作以及代理人作答等原因，调查获得的数据不一定准确，存在一定回应误差。如何消除回应误差成为准确估算人力资本收益率的难题。本文在上述学者的研究基础上，深入研究标准化数据不可得情况下收入方程的回应误差问题，并以此为依据考察估算人力资本收益率的最佳方法。

二、收入方程优化及估算方法研究

(一)收入方程优化

本文将收入方程设定如下(见式(1))。

式(1)中，

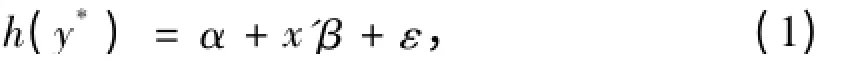
h

代表未特指的收入方程，

y

代表因变量，

x'

代表协变量，ε代表与协变量

x'

不相关且服从零均值和同方差正态分布的随机变量，在

x'

给定条件下，ε的条件均值为0。为了在收入方程中包括回应误差，假定可观测到

y

存在服从零均值和同方差正态分布的回应误差(η)。

就式(2)而言，

E

(η

x'

，ε)

=

0，如果

h

代表线性收入方程，由于

x'

给定条件下

y

的条件期望不受回应误差影响，即

E

(

y

x'

)

=E

(

y

x'

)，普通最小二乘回归估计值与实际值一致。这是国内外学者利用明瑟收入方程使用普通最小二乘估算人力资本收益率的理论基础。如果

h

不是线性函数，

E

(

h

(

y

)

x'

)和

E

(

h

(

y

)

x'

)的条将期望不一定相同，

h

(

y

)对

x'

的最小二乘回归估计值与实际值不一致。如果

h

连续可微，合并式(1)和式(2)可得: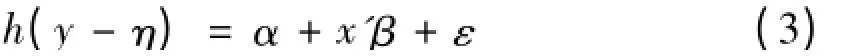

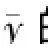
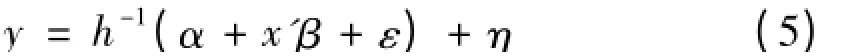
本文基于式(5)体现的反函数思想考察不同估计策略。首先，就对数收入方程而言，式(5)某种程度上的简化，使最小二乘方法直接可用。其次，就参数化波克斯考克斯转换而言，一个泰勒展开式能够用作

x'

给定时逼近

y

的条件均值和进行非线性最小二乘估算的理论基础。为了阐明这一观点，本文首先考虑收入方程为对数转换情况，选择对数收入方程作为分析的起点是由于明瑟收入方程的对数转换有着其他收入方程所没有的优点:首先，明瑟收入方程的对数转换具有代表性，它是基于个人理性的最优市场行为，代表了市场机制发挥作用的结果;其次，对数转换的明瑟收入方程将难以估算的变量转变成为可估算的变量，可以对教育水平和工龄对个人收入的影响进行定量分析，即将人力资本投资的货币投入成本变为教育水平和劳动力市场经验(工龄)等可估算的机会成本;再次，对数转换的收入方程中可以包括其他影响收入的变量，可以考虑机会、能力等因素对收入的影响;第四，对数转换的明瑟收入方程中相关变量的系数估计值能够解释教育水平和工龄的经济意义，这些系数估计值和系数的标准误差估计值允许随着时间和空间的变化作比较;第五，尽管收入分布服从正偏态、收入不平等随着教育程度和工龄的增加而增加，但是，通过将收入取自然对数后作为因变量，收入的残差接近标准正态分布;最后，对数转换的明瑟收入方程能够用于估算收入的相对不平等，收入的对数方差，有利于收入和收入不平等在不同时间和空间的比较。假定ε的分布独立于

x'

，在对数收入方程下，普通最小二乘和非线性最小二乘回归仍可用于估计人力资本收益率。令

h

(

y

)

=

ln

y

，式(5)变为

由于η服从零均值和同方差的正态分布，对式(6)取数学期望，可将式(6)转换为

令

式(7)可转换为

E

(

y

x

)

=Ce

，由于ε服从零均值和同方差的正态分布，式(8)可以转化为

当式(5)未出现收敛时，需要考虑参数化博克斯考克斯收入方程，就参数收入方程(博克斯考克斯收入方程)而言，一个泰勒展开式能够用作

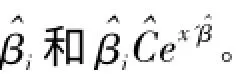
x'

给定时逼近

y

的条件均值和进行非线性最小二乘估算和极大似然估计的理论基础。本文将博克斯考克斯收入方程写作

h

(

y

)=

h

(

y

，λ)

.

如果

h

已知，可忽略λ。为了简化，令

g

(ν，λ)代表收入方程的反函数(即定义

g

(ν，λ)=

y

，⇔

h

(

y

，λ)=

v

)，

g

(

v

，λ)代表

g

(

v

，λ)对

v

的第

j

次导数。式(5)的数学期望为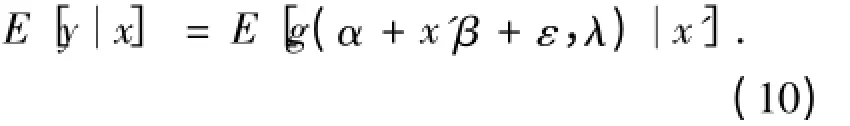

假定

g

代表(

d

+1)次连续微分，基于泰勒展开式可知存在一个函数

t

(ε)，

t

(ε)满足

在附加假定下，ε对称，对于奇次项(

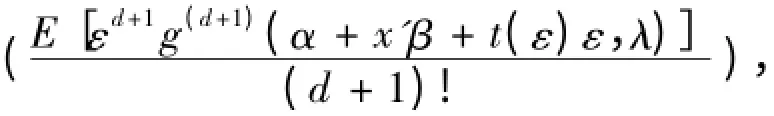
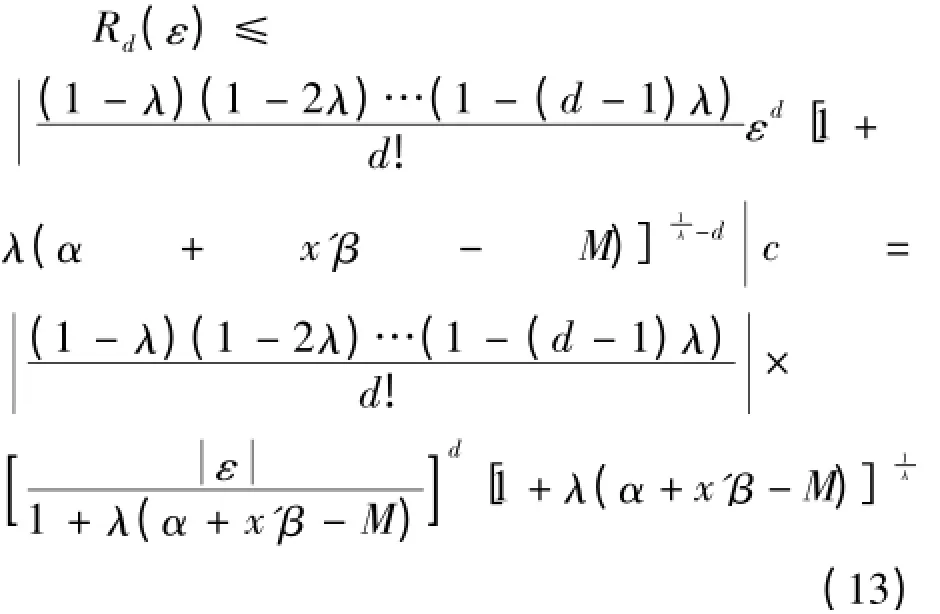
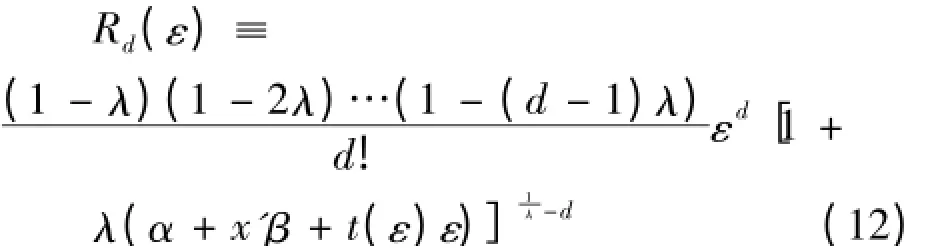
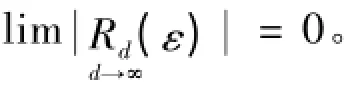
j

)，［ε］

=

0，以至于每隔一项，在式(11)和(14)的展开式中去掉一项，由于ε

～N

(0，σ)，表明对于偶数项(

j

)，

E

(ε)

=

σ(

j-

1)(

j-

3)…3·1，强化正态假定特别有帮助。式(14)展开式中的矩数是参数σ的函数，附加多余的参数不需要附加展开项。在正态假定下，可将式(14)续写为: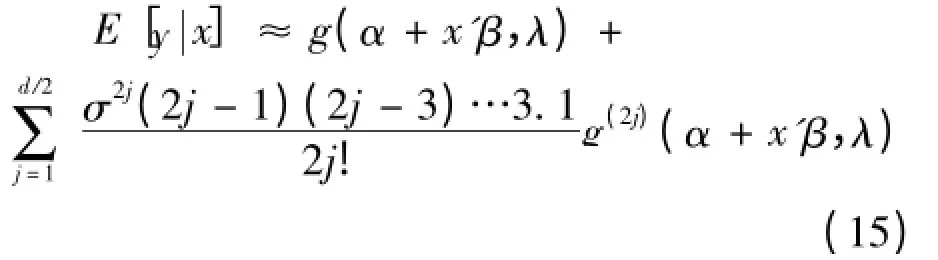

这一部分的余项集中在博克斯考克斯收入方程中，λ位于(0，1)之间

就博克斯考克斯收入方程来说，

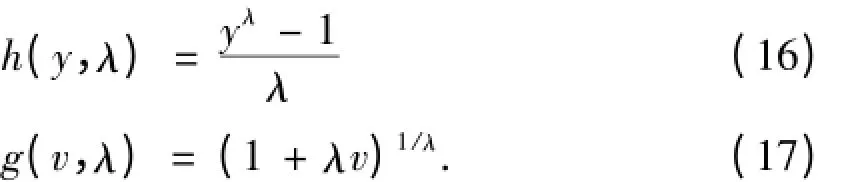
g

(

v

，λ)的推导结果是

为了对博克斯考克斯收入方程进行极大似然估计，正态假定是最好的估计方法，结合式(15)和式(18)可得

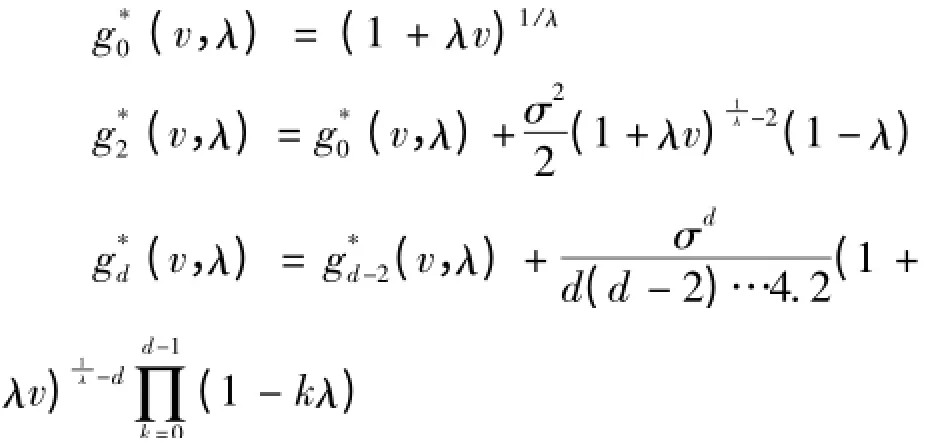
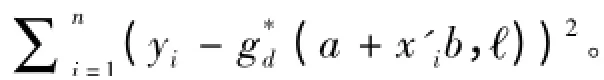
(二)博克斯考克斯极大似然估计和非线性最小二乘估计

基于博克斯考克斯收入方程在经验研究中的优势，首先考察当博克斯考克斯收入方程给定时，泰勒逼近法多大程度上逼近条件期望。这一考察不需要模拟，因为这一考察仅需要在给定的泰勒展开式项数既定的选择下评价式(15)，σ，λ的实际值可用于比较逼近条件期望和实际条件期望

E

(

y

x

)。其次，考察泰勒逼近非线性最小二乘估计值(展开式项数不同)的作用和博克斯考克斯极大似然估计值的关系。

博克斯考克斯收入方程(λ≠0)可续写为:

式(19)中，υ≡α

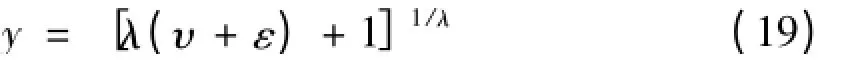
+x'

β，条件期望是:

式(15)中泰勒逼近是否与式(18)逼近，取决于υ，σ(ε的方差)和λ(非线性参数)。就模拟而言，本文考察与λ=0.2、λ=0.5和λ=0.8相应的三个不同博克斯考克斯收入方程设定。结合三个博克斯考克斯收入方程设定，在假定三个博克斯考克斯收入方程设定都存在回应误差的情况下，使用2008年黑龙江省哈尔滨、齐齐哈尔、牡丹江、佳木斯和大庆5城市的样本做了200个模拟，每一模拟使用四个不同的估计量，即一个极大似然估计量和三个泰勒逼近非线性最小二乘估计量(分别是泰勒一阶、二阶和三阶展开式)。

表1列出模拟结果和每一设定

^

λ的均值和均方根误差。此外，由于本文研究的重点是估计条件期望，因此列出基于

x

五个不同点(

x

取值分别为5，10，15，20，25)的条件期望估计值均方根误差比。均方根误差比被定义为一个既定估计量的均方根误差除以极大似然估计量的均方根误差。令极大似然估计量的均方根误差比都等于1。均方根误差比低于(高于)1说明估计量比极大似然估计量(使用均方根误差标准)有更多(更少)精确的预测值。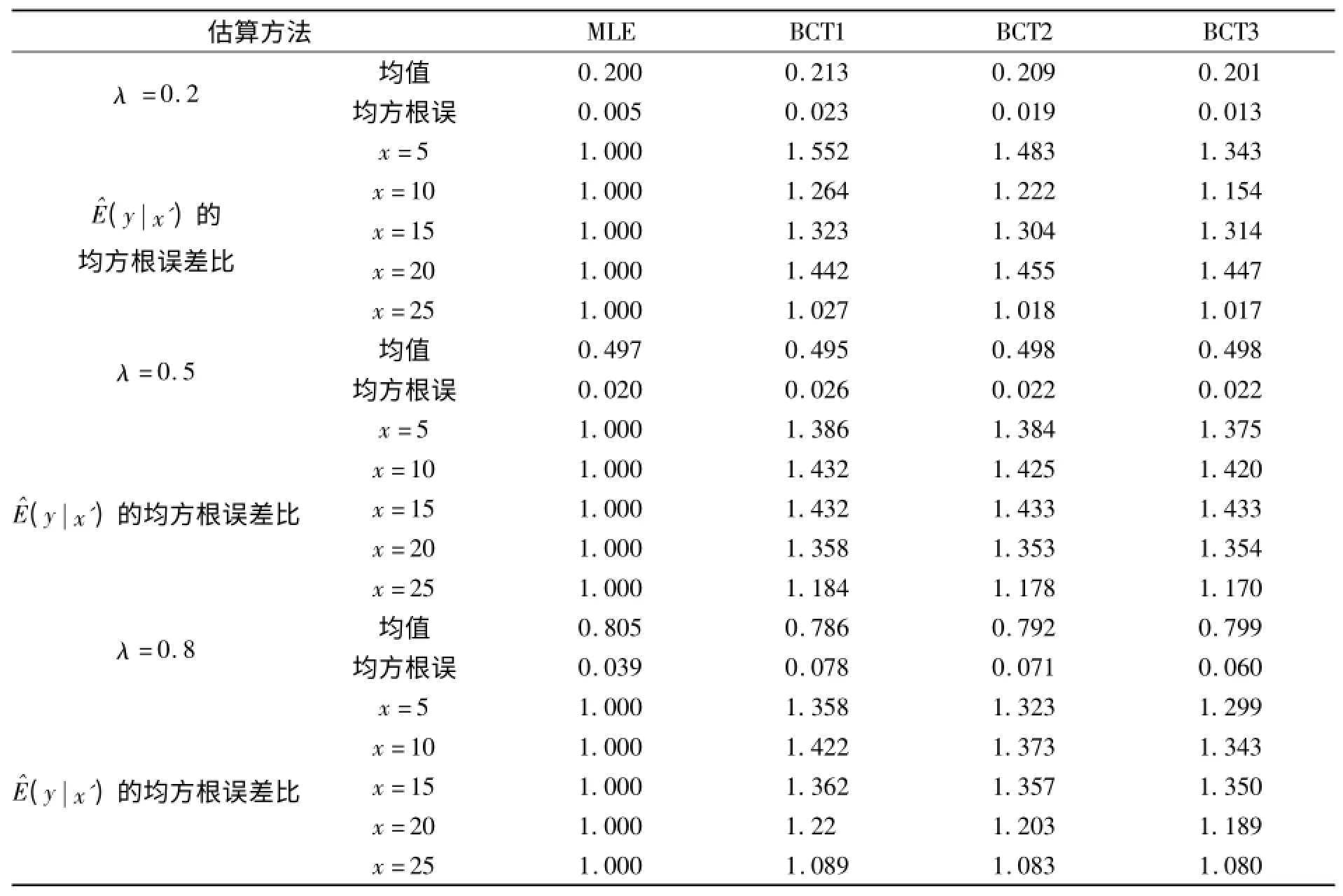

表1 博克斯考克斯模拟结果

对于三个博克斯考克斯设定，由表1归纳如下:

(1)极大似然估计法是估算人力资本收益率的最佳方法。由表1可知，与博克斯考克斯泰勒逼近一阶(BCT1)、二阶(BCT2)和三阶(BCT2)非线性最小二乘估计相比，极大似然估计(MLE)具有较低的既与λ又与不同的条件期望有一定联系的均方根误差估计值。例如，λ=0.2时，极大似然估计均方根误差估计值为0.005，而泰勒逼近一阶(BCT1)、二阶(BCT2)和三阶(BCT2)非线性最小二乘估计均方根误差估计值分别为0.023，0.019和0.013。λ=0.5时，极大似然估计均方根误差估计值为0.020，而泰勒逼近一阶(BCT1)、二阶(BCT2)和三阶(BCT2)非线性最小二乘估计均方根误差估计值分别为0.026，0.022和0.022。λ=0.8时，极大似然估计均方根误差估计值为0.039，而泰勒逼近一阶(BCT1)、二阶(BCT2)和三阶(BCT2)非线性最小二乘估计均方根误差估计值分别为0.078，0.071和0.060。因此，极大似然估计可能比博克斯考克斯泰勒逼近非线性最小二乘估计更有效。

(2)泰勒逼近三阶展开式是估算人力资本收益率的最佳收入方程。随着泰勒逼近展开式项数逐渐增加，均方根误差估计值逐渐减小，这是由于博克斯考克斯泰勒展开式估计量被明确定义为最小化非线性最小二乘估计，在回归函数中增加项数会改善样本内预测效果。表1中均方根误差与样本外预测有关(例如估计量估计的实际条件期望程度如何)。通常考虑估计量存在方差偏差权衡问题(这一估计量在回归函数中有效地增加了展开项)。在此，随着展开式项数增加，方差逐渐减少，但是偏差会增加。

(3)在模型的非线性特征方面，极大似然估计优于泰勒逼近非线性最小二乘估计。由表1可知，

x

取值不同，估计量的效果也不同。例如，λ=0.2时，极大似然估计在每一个

x

值(除了

x

等于25)上都优于博克斯考克斯泰勒逼近非线性最小二乘估计值，在

x

=25时，估计量几乎等于展开式项数。

三、经验研究

(一)数据来源与描述性统计

本文使用的数据来自对黑龙江省内5城市的问卷调查，调查时间为2008年7月至9月，以在校大学生为调查者，利用暑期在校大学生回乡时间，组织在校大学生深入到各地市做问卷调查，采取简单随机抽样方法，随机走访当地居民，调查对象是处于就业状态的城乡劳动力。调查信息包括年龄、教育水平(受教育年限)、工龄、个人收入等指标。本文选取了哈尔滨、齐齐哈尔、牡丹江、佳木斯、大庆5个地级单位的调查数据，在上述5个城市共发放问卷38000份，回收38000份，其中有效问卷37580份，占回收问卷总数的98.87%，男性样本20574份，占样本总数的52.55%，女性样本17006份，占样本总数的47.45%，样本月平均收入1447.65元，平均年龄38.64岁，平均受教育年限12.24年。

在每一教育水平内部，根据样本年龄分布情况，将工龄界定在1年至40年之间。“个人收入”被定义为一个连续变量，测算中由月工资收入代表。根据问卷反馈信息，按照地区和工龄分组，计算每一地区中每一工龄的不同教育水平样本平均收入，将数据压缩成800个单元(5个城市乘以40个工龄再乘以4个教育水平)。在800个单元中，共有37580个个体观测值，哈尔滨的个体观测值最多(9856个)，大庆市的个体观测值最少(4542个)。在每一单元中，个体观测值最少为11个(大庆市工龄为34年的小学样本观测值为11个)，个体观测值最多为324个(哈尔滨工龄为15年的高中样本观测值为324个)，表2给出本次问卷调查样本基本情况。

从总体上看，收入较低，其中，月收入低于800元的样本占样本总数的11.24%，月收入介于800～1200元之间的样本占样本总数的25.46%，月收入介于1200～2000元之间的样本占样本总数的36.45%，月收入高于2000元的占样本总数的26.85%。根据不同教育水平样本统计，高中学历样本数较多，占样本总数的35.86%，其次为大学学历样本(33.89%)和初中学历样本(19.74%)，小学学历的样本数最少，占样本总数的10.48%。在每一教育水平内部，按照不同工龄划分，将样本分为0至10年工龄、10至25年工龄和25至40年工龄三个时间段。小学学历、初中学历和高中学历的样本中工龄介于25至40年的偏多，分别占相应教育水平样本数的5.97%(该教育水平样本占样本总数的10.48%)、9.31%(该教育水平样本占样本总数的19.74%)和14.82%(该教育水平样本占样本总数的35.86%)，而大学学历样本中，工龄介于0至10年的样本偏多，占相应教育水平样本数的11.05%(该教育水平样本占样本总数的33.89%)。

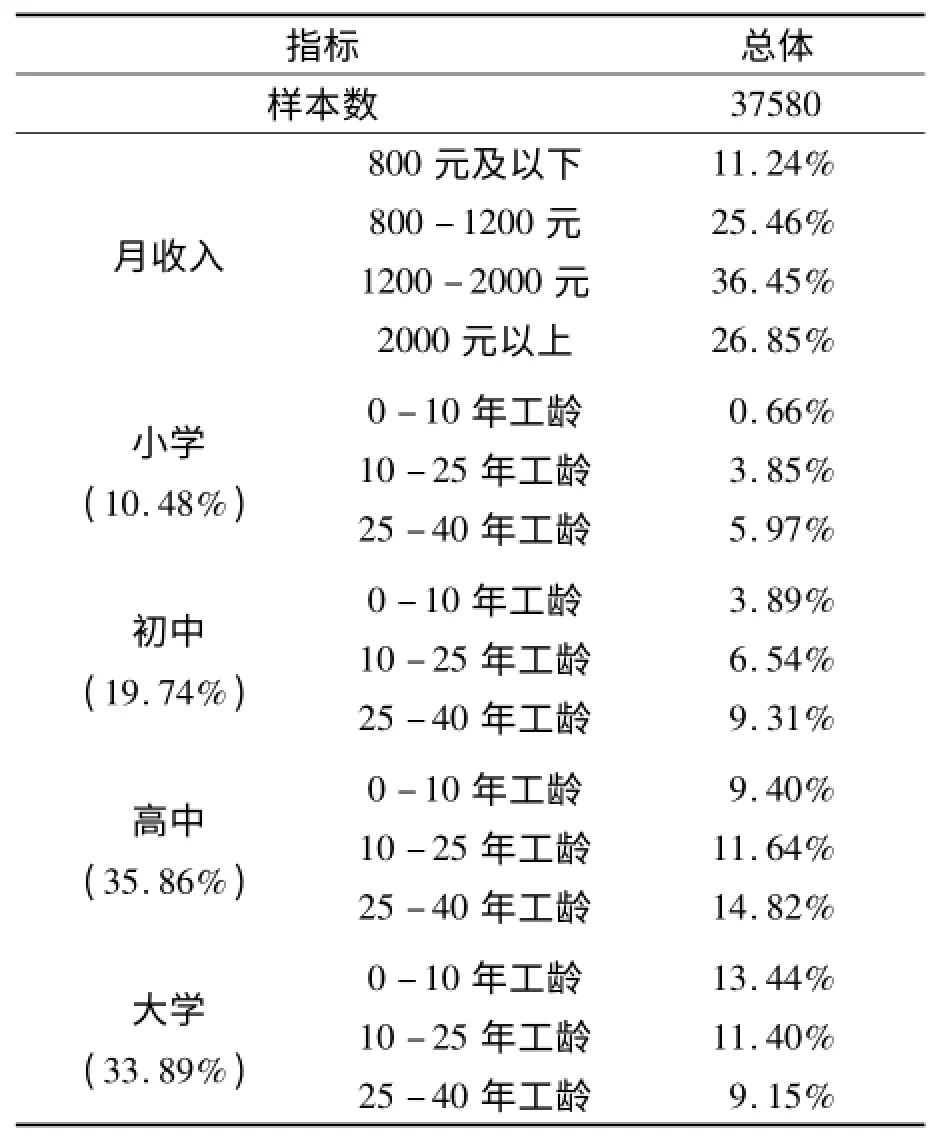
表2 5城市问卷调查样本基本情况描述性统计%

(二)实证检验

在标准明瑟收入方程中，月收入对数被设定为受教育年限、工龄和工龄平方项的线性函数。

与式(1)不同，式(21)中，ln

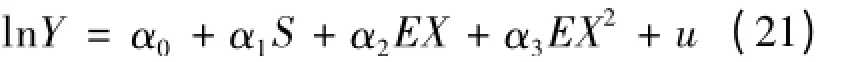
Y

代表收入方程(1)中的因变量

y

，

S

、

EX

、

EX

代表协变量

x'

，

S

、

EX

、

EX

、

u

分别代表收入的自然对数、受教育年限、工龄、工龄平方项和误差项，α代表常数项，α、α和α分别代表受教育年限、工龄和工龄平方项的系数估计值。

最早从理论和实证角度对明瑟收入方程中工龄变量二次设定提出置疑的是墨菲和韦尔奇(Murphy，Kevin M，and Welch，Finis)，他们在实证研究中发现，明瑟收入方程对于工龄与收入之间关系二次设定的描述不准确，低估了个人职业生涯早期大约30%至50%的收入增长，高估了职业生涯中期大约20%至50%的收入增长。在阐述由工龄变量二次设定引起的偏差时，墨菲和韦尔奇指出，在收入方程中加入工龄变量的高阶项是解决工龄变量二次设定引起的偏差的有效方法，经验研究发现，加入工龄三次设定后，收入方程的残差显著减少。王云多使用问卷调查获得的截面数据研究工龄二次设定引起的偏差，通过在工龄二次函数中加入工龄高阶多项式消除偏差，实证分析结果表明，工龄三次函数是测量收入剖面的最优选择。消除了几乎所有由工龄二次函数产生的残差，近似反映实际收入剖面。

基于上述学者的理论及实证研究，以及本文在考察博克斯考克斯展开式估计时得出的泰勒三阶展开式是估算人力资本收益率的最佳方程，本文在标准明瑟收入方程中加入了工龄三次项和一个工龄乘以受教育年限的交互项，设定如下。

与式(21)不同，式(22)中

EX

3和

S

*

EX

分别代表工龄三次项和受教育年限与工龄交互项，α、α、α、α和α分别代表相应变量的系数估计值。为了比较本文研究的不同替代方法，本文考察了二个不同的被用于工资变量的收入方程(

h

)处理。第一个处理假定收入方程为对数转换(

h

(·)≡ln(·))，适用于普通最小二乘和非线性最小二乘估计量。第二个处理假定收入方程属于博克斯考克斯转换，适用于博克斯考克斯极大似然估计。

表3列出对数线性和博克斯考克斯收入方程的参数估计值，括号中数值为标准误。可得到对数工资的普通最小二乘和非线性最小二乘估计值，以及博克斯考克斯收入方程极大似然估计值。非线性最小二乘估计值把基于式(7)的一个最小二乘目标函数减少到最低程度，估算结果表明:

表3 参数估计

(1)极大似然估计是估算人力资本收益率的最佳方法。由表3可知，无论是使用式(21)还是式(22)，博克斯考克斯极大似然估计的λ参数统计上都显著，意味着统计上拒绝了对数线性模型。

(2)使用标准明瑟收入方程低估了教育收益率和工龄收益率。由表3可知，与式(21)相比，基于使用加入工龄三次项和教育年限与工龄交互项的式(22)，采用极大似然估计法估计的教育收益率(0.1323)和工龄收益率(0.0726)高于基于式(21)的教育收益率(0.1090)和工龄收益率(0.0325)极大似然估计值。

(3)普通最小二乘估计和非线性最小二乘估计低估了教育收益率和工龄收益率。由表3可知，无论是使用式(21)还是式(22)，采用极大似然估计法估计的教育收益率和工龄收益率都要高于使用普通最小二乘和非线性最小二乘估计的教育收益率和工龄收益率。

四、结 论

本文研究了处理收入方程因变量回应误差的方法，直接根据因变量续写了收入方程，使用黑龙江省5城市问卷调查数据估算了因变量存在回应误差情况下的条件期望，研究结论如下:

(1)泰勒三阶展开式是估算人力资本收益率的最佳转换形式。研究表明，随着泰勒逼近展开式项数逐渐增加，均方根误差估计值逐渐减小，这是由于博克斯考克斯泰勒展开式估计量被明确定义为最小化非线性最小二乘估计，在回归函数中增加项数会改善样本内预测效果。

(2)存在因变量回应误差时，极大似然估计是最有效的估计方法，普通最小二乘和非线性最小二乘估计无效。与博克斯考克斯泰勒逼近一阶(BCT1)、二阶(BCT2)和三阶(BCT2)非线性最小二乘估计相比，极大似然估计(MLE)具有较低的既与λ又与不同的条件期望有一定联系的均方根误差估计值。

(3)普通最小二乘估计低估了教育收益率和工龄收益率。实证检验中，加入工龄高阶项后收入方程拟合度有显著提高，而教育收益率和工龄收益率有所提高。

［1］Heckman，J，Jand Polachek，S..Empirical evidence on the function form of the earnings-schooling relationship［J］.Journal of the American Statistical Association，1974，(69).

［2］Horowitz，J.L..Semiparametric estimation of a regression model with an unknown transformation of the dependent cariable［J］.Econometrica，1996，(64).

［3］Chen，S.，Lockhart，R.A.and Sherman，M.A..Box-Cox transformation in linear models:Large smple theory and tests of normality［J］.Canadian Journal of Statistics，2002，(30).

［4］Chen，S..Rank estimation of transformation models［J］.Econometrica，2002，(70).

［5］Klein，R.W.and Sherman，R.P..Shift restrictions and semiparametric estimation in a generalized transformation model［J］.Econometrica，2002，(70).

［6］Abrevaya Jason and Hausman.Jerry A.Response error in a transformation model with an application to earning-equation estimation［J］.Econometrics Journal，2004，(7).

［7］王明进，岳昌君.个人教育收益率的估计与比较:一个半参数方法［J］.统计研究，2009，(6).

［8］赵西亮，朱喜.城镇居民的大学教育收益率估计:倾向指数匹配方法［J］.南方经济，2009，(10).

［9］Wooldridge，J.M..Some altermative to the Box-Cox regression model［J］.International Economic Review，1992，(33).

［10］Murphy，Kevin M，and Welch，Finis..Empirical Age-Earning Profiles［J］.Journal of Labor Economics，1990，(18).

［11］王云多.试析地区、行业和性别因素对人力资本收益率的影响［J］.人口与经济，2009，(6).