EMD过程中数据拟合的算法改进与实现*
寇艳廷,范涛涛,刘 晨,阎红灿
(河北联合大学 理学院,河北 唐山 063000)
希尔伯特—黄变换HHT(Hilbert-Huang Transform)是1998年由Huang等人[1-2]提出的一种信号分析方法,它通过经验模态分解EMD(Empirical Mode Decomposition)基于信号的局部特征时间尺度将信号分解成有限数目的本征模态函数 IMF(Intrinsic Mode Functions)之和,对每个IMF进行Hilbert变换可以求得具有物理意义的瞬间频率,非常适合对非平稳信号处理。所以许多研究学者将该技术应用于数据波的时频分析[3-4]和时间序列的预测研究[5-6],取得了显著的成果。
时间序列模型适合于线性时序的预测,当用于预测非线性时间序列时,准确性较差;小波分析方法中数据基本假定为平稳序列,当用于非平稳时间序列预测时准确性不高;神经网络具有逼近非线性的能力,然而当用神经网络来预测股价时间序列时,其结果不是很理想;中国证券市场的混沌性暗示着金融时间序列的长期不可预测性和短期预测的可行性,但混沌模型与其他方法对股市进行预测时,也未能得到令理论界和实务界较满意的效果。在研究金融数据预测时提出了将EMD与神经网络结合的预测模型,就是利用EMD处理非平稳数据的优势。
在EMD过程中,最为关键的就是如何拟合成与原始数据逼近的函数,即构造函数的算法问题。而要想构造较为准确的函数,关键是包络线的选取算法。现有的EMD分解算法一般应用三次样条插值法,虽然能够得到较为理想的结果,但仍然有些偏差,特别是边缘数据(拐点)误差较大。本文系统分析了三次样条插值算法和分段幂函数插值算法的特点,将其结合找到一种更好的求包络线的算法,从而提出了一种更为有效的数据拟合函数构造方法。
1 经验模态分解(EMD)
1.1 本征模态函数性质
EMD算法的目的就是将复杂数据(信号)分解为有限个本征模态函数IMFs,这里IMF须满足如下两个性质:
(1)信号的极值点(极大值或极小值)数目和过零点数目相等或最多相差一个;
(2)由局部极大值构成的上包络线和由局部极小值构成的下包络线的平均值为零。
1.2 EMD算法简介
EMD算法步骤如下:
(1)计算出信号 s(t)所有的局部极值点。
(2)求所有的极大值点构成的上包络线和所有的极小值点构成的下包络线,分别极为 u0(t)和 v0(t)。
(3)记上、下包络线的均值为:

(4)判断 h0(t)是否满足 IMF的上述两条性质。若满足,则 h0(t)为 IMF;否则,记 h0(t)为 s(t)。 重复步骤(1)~步骤(3),直到得到一个 IMF,记为 C1(t)。
(5)记 r1(t)=s(t)-C1(t)为新的待分析信号,重复步骤(1)~步骤(4),以得到第二个 IMF,记为 C2(t),此时余项 r2(t)=r1(t)-C1(t)。 重复上述步骤,直至得到的余项 rn(t)是一个单调信号或 rn(t)的值小于预先给定的阈值,分解结束。
如此,最终可得到 n 个 IMFs,C1(t),C2(t),…,Cn(t)余项为 rn(t)。 因此,原信号 s(t)可表示为:

2 分段幂函数插值算法的应用
EMD算法的核心部分就是求解包络线算法,现有的技术一般采用三次样条插值法。由于边缘数据(端点)选取直接影响数据拟合效果,如果样条插值中端点的选取再精确些,就会得到更好的拟合数据点,而分段幂函数具有端点延拓的特点,对边缘端点有平滑处理功能,弥补了样条插值法的缺陷。本节详细讨论分段幂函数插值在求解包络线中的应用。
2.1 算法原理及分析
记所有的插值点 P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),插值函数 y=f(x)。对任意 3 个相邻点 Pi-1(xi-1,yi-1),Pi(xi,yi),Pi+1(xi+1,yi+1)进行幂函数插值:

分段幂函数插值算法的误差范围随β的增大而减小,且误差的最大范围为[Mh2/2.5,5Mh2/2]。
2.2 算法实现

3 实验仿真
结合实际数据,利用Matlab数学软件进行实验仿真,表1是实验仿真的测试数据。

表1 数据记录表
3.1 利用三次样条插值函数绘制图像
选择Matlab内置函数spline,先编写主函数,核心代码如下:

以文件名yangtiao_main.m保存。运行程序,得到运行结果如图1和图2所示。
3.2 利用分段三次样条插值保形:
主函数核心代码: %分段三次Hermite插值法主函数

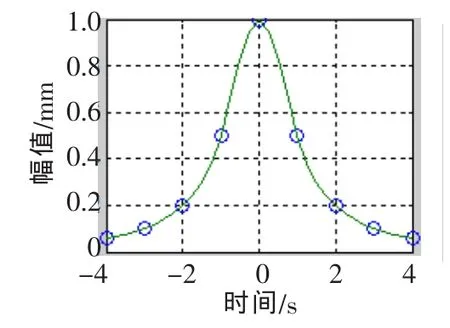
图1 三次样条插值采样点

图2 三次样条插值拟合结果
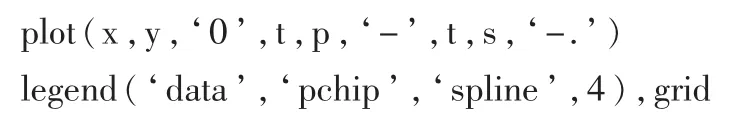
运行程序,结果如图3和图4所示。

图3 分段幂函数采样点

图4 分段幂函数拟合结果
3.3 实验分析
从图1可以看出,经过分段幂函数的端点延拓处理,插值拟合的函数更接近于原始数据,大大提高了EMD中数据拟合的效果。为下一步数据分析和预测提供了技术保证。
本文在分析经验模态分解算法的基础上,讨论了三次样条插值求解包络线的弊端,引入分段幂函数端点延拓技术,提高了数据拟合精度。实验表明,对数据拟合算法的改进极大提高了EMD过程中函数拟合的效果,有利于提高时间序列分析和预测精度。
[1]HUANG N E, Shen Zheng, LONG S R, et al.The empirical mode decomposition and the Hilbert spectrum for non-linear and non-station time series analysis[J].Proc R SocLond,1998,45(4):903-995.
[2]HUANG N E, Shen Zheng, LONG S R.A new view of non-linear water waves.The hilbert spectrum [J].Annual Review of Fluid Mechanics,1999,31:417-457.
[3]盖强.局域波时频分析方法的理论研究与应用 [D].大连:大连理工大学,2001:52-54.
[4]徐世艳.经验模态分解的时频分析方法及其应用[J].吉林大学学报,2009,9(27-5):487-492.
[5]刘慧婷,倪志伟,李建洋.经验模态分解方法及其应用[J].计算机工程及应用,2006,32(1):44-47.
[6]玄兆燕,杨公训.EMD在地面气温预测中的应用 [J].微计算机信息,2008,2(24-3):230-232.

