铁路行业并购的超越对数成本函数检验

袁 欣，张秋生

（1.中国企业兼并重组研究中心；2.北京交通大学经济与管理学院，北京100044）

0 引言

并购是现代市场经济正常的活动，并在市场经济机制中发挥不可替代的作用。中国铁路目前是由铁道部直辖的18个基本上按照中国省市行政区域划分的路局组成。随着目前中国铁路“客货分离”模式的建立和不断深化，铁路货运将进入大规模并购重组时代。如何检测铁路企业并购重组成本变化？是否每一次并购重组活动都能获得正向的协同效应？能否建立成本函数模型来检验铁路企业并购前后成本的变化，并验证铁路企业的规模经济临界点。

1 超越对数成本函数

本文选择超越对数成本函数来检验铁路成本。

单一产品生产企业都可以用生产函数Y=f(x)来描述。其中x代表投入变量，Y=f(x)代表不同投入变量x所对应的企业Y产品产出可能性组合的合集。然而铁路是多产品行业，一个真正的多产品的行业，不能用单一产品的生产函数来描述，也不能用线性生产函数来描述。类似多产品企业的生产函数是一个变换函数。变换函数主要体现的是通过制定有效的生产计划，在投入固定的限定下，使产出最大化。

变化函数一般表示为T（x，y）=0，其中y是产出变量，x是投入变量。在x为给定且y取得最大值时，这个变换函数等于0。

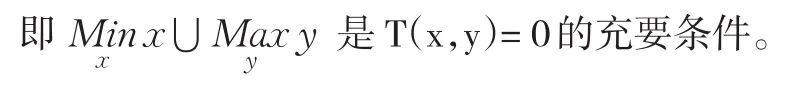
而选择超越对数成本函数可以用来研究多产品生产企业的成本弹性变动情况。超越对数成本函数的最大特点就是其具有灵活性。超越对数是一种易于估计和包容性很强的变弹性生产函数模型，它在结构上属于平方反映模型，可有效研究生产函数中投入要素的相互影响。超越对数允许对成本函数进行预估而不加以限定。

两种投入变量的超越对数成本函数表示为：

研究如上述成本函数的未知方程的一个方法就是对余数进行泰勒级数展开。Friedlaender和Spady(1980)的研究显示，超越对数成本方程可以是一个随意函数的二阶泰勒级数展开。对于广义的铁路成本函数的四个要素，价格要素、产出要素、资本存量、技术要素作二阶泰勒级数展开，可得：

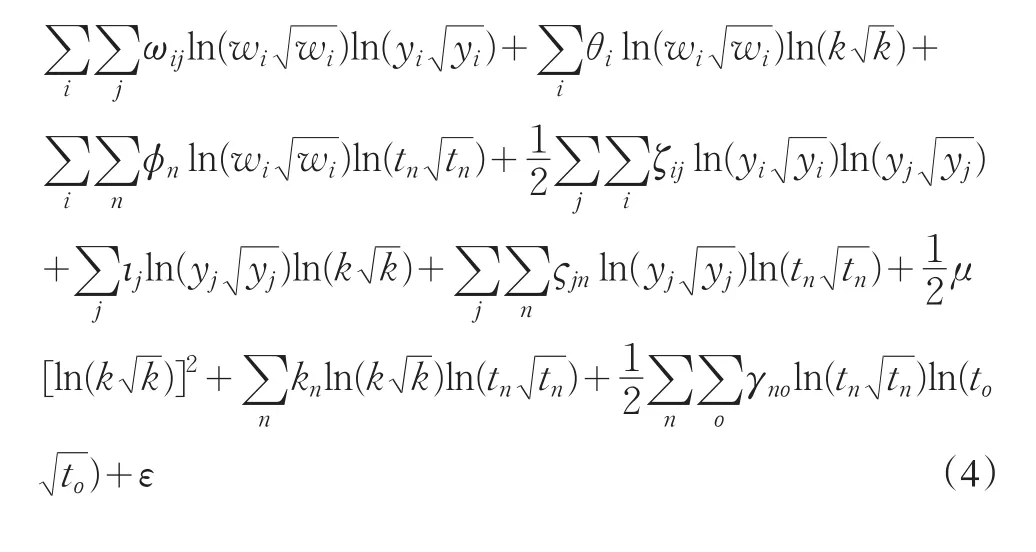
2 铁路并购案例的超越对数成本函数实证

2.1 样本和数据

美国铁路始建于1827年，从第一条巴尔的摩到俄亥俄州全长13英里的铁路，演化到2010年超过26万英里纵横交错的铁路网络。铁路公司之间不断并购重组，美国铁路公司的数量也由高峰期的超过6000家，到2005年下降为560家。美国铁路由割裂的小网络，通过并购连结成具有包含横贯东西、纵穿南北的主干线和大量支线组成的非均质网络。美国铁路网络的形成历史就是网络并购演进的历史。并且美国铁路有近200年的演进历史，数据详实。因此本文选取美国铁路作为研究对象。

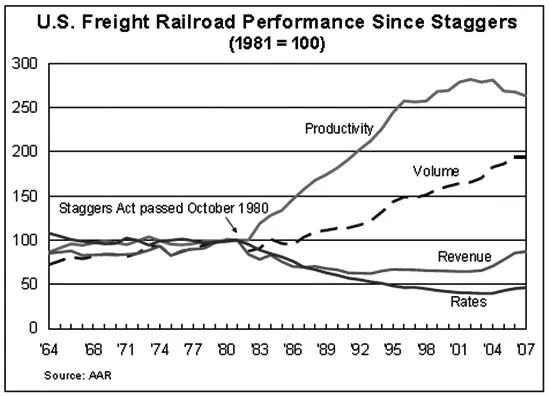
图1 美国铁路货运指标（1964～2007）

图1展示了美国铁路货运指标的变化，是以1980年作为基准点100。从图中可以看出，铁路货运的生产率在1980年之后有了显著增长。从1980年美国《斯塔格斯铁路法》颁布，对美国铁路公司的并购重组管制放松后，美国铁路进入复兴时代，随着铁路公司数量减少的同时，铁路货运量和生产率都大幅提高。因此本文选取了1980年后的样本，选取从1983～1997年美国铁路公司实际发生的215起并购案作为研究样本。数据来源于美国州际商务委员会年度报告（1983～1997）。

2.2 美国铁路超越对数成本函数

美国铁路的长期成本可以表示为各要素的函数：

其中：wl为劳动力价格，wm+s为原材料价格，wf为燃油价格，we为设备价格，wi为工务部门价格，utgtm为单列车运行总吨公里，wtgtm为慢车运行总吨公里，ttgtm为直达列车运行总吨公里，mor为运行里程，alh为平均运输距离，speed为列车时速（英里/小时），time为时间（小时）。

对公式(4)方程两边求偏导数,并用变量代替偏导数，并代入误差项。

则美国铁路超越对数成本函数可以表示为：

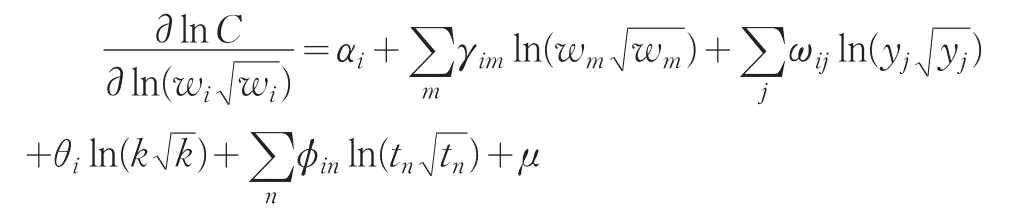
表1 成本函数超越对数的似乎不相关回归和分配控制变量方程对企业的影响

表1显示了美国铁路成本函数的预估结果。可以看出，在铁路成本要素中，劳动力价格，道路投资，原材料投入，分别占到铁路总成本的34.5%、25.6%和18.6%。设备和燃油成本占总成本的14.8%和6.6%。

由于不同的成本变量具有不同的弹性，不同的成本变量形成一个数值的产出，可能会导致成本变量和产出变量对应关系的扭曲。为了研究将吨英里作为唯一的输出变量而对应的受限均质弹性成本是否合理，对超越对数生产函数进行F检验。

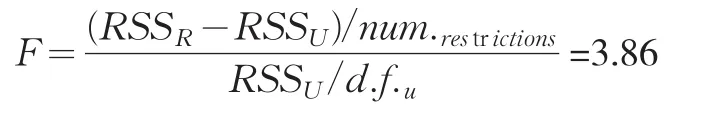
其中：RSSR为无限制的残差平方和，RSSU为受限制的残差平方和，d.f.u为无限制模型的自由度。

F检验显示，使用多重输出变量，对模型的结果有显著的提高，而多重成本变量具有均一弹性的假设，对相对应的输出变量是无效的。

此外，价格要素、路程里程也对输出变量具有显著影响。在路程里程增加1%，而对应的成本则上升0.56%。速度对产出具有显著效应，但是在道路基本建设上投入的成本，在常规的水平是不显著的。最后时间序列表明，美国铁路总成本的投入量基本上按照2.8%的比率在逐年递减。

3 次可加性检验

企业的并购协同一般分为经营协同、财务协同、管理协同等。规模经济和范围经济都对企业并购活动所取得的协同效应产生重要影响。为了评估规模经济和范围经济在铁路并购案例中的影响，用次可加性对美国铁路成本函数进行了验证。函数的次可加性是函数的一个性质，它证明计算函数对定义域中两个元素的和总是返回小于等于这个函数对每个元素的值的和的某个值。

即一个函数f：A→B，其定义域A和陪域B上分别定义了某种加法+A和+B，且陪域B上定义了偏序关系“≤”。若该函数满足：∀x,y∈A，有 f(x+Ay)≤f(x)+Bf(y)。则称f对于+A和+B满足次可加性。在上下文对于+A和+B都很明确的情况下，通常简称为f满足次可加性，亦称f为次可加函数。

在美国铁路并购案例中，次可加性被用于检验两个企业并购前和并购后的生产成本对比。为了验证规模经济和范围经济对并购前后铁路成本函数变动的影响，本文模拟两种不同的情景对成本函数进行次可加性测试。第一种模拟是保持铁路网络规模恒定，即并购前和并购后的美国铁路网络规模不变，将单列车、慢车、直达列车的吨英里作为输出变量，模拟两个企业并购前和合并为一个企业时成本次可加性。这相当于并购发生后，两个公司合并成为一个新的公司，作为并购前两个独立公司的替代在固定网络规模内提供服务。第二种模拟测试允许并购前后的铁路网络规模发生变动，将单列车、慢车和直达列车作为输出变量，评估并购前多企业独立运营企业和并购后形成的一个企业运营间的成本差异。对于产出固定、网络规模并购前后也固定的并购案例来说，网络规模较小，产能过剩处于规模不经济生产状态的企业并购会获得规模经济。

测试次可加性，用公式可以表示为：

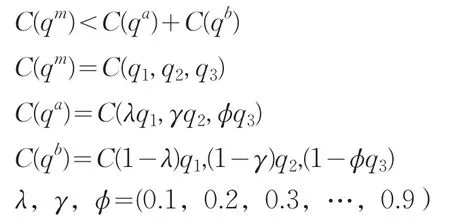
q1,q2,q3分别为单列车、慢车和直达列车

用来测算并购后一个企业和并购前多个企业次可加性的参数λ，γ，φ来自于超越对数成本函数。对于所选的215样本，分裂输出365个向量组合，因此在网络规模恒定的情况下，共计有78475种组合需要模拟。

表2列出了当网络规模不变时对成本次可加性模拟检验的结果。在1983年的成本模型中，215个样本中有201个具有次可加性。即在假设并购前后生产网络的规模保持不变的前提下有201起并购案并购后单一企业的生产成本小于并购前多个企业的生产成本。

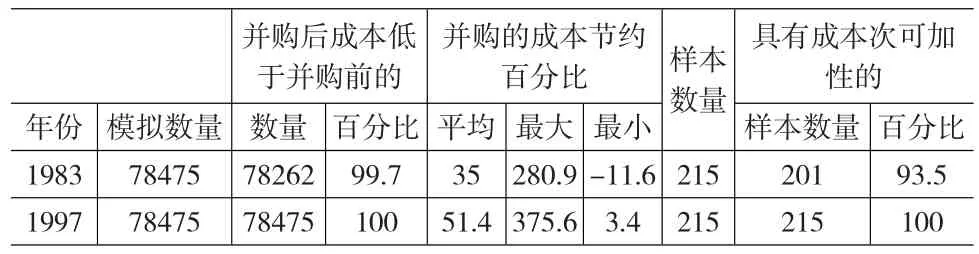
表2 网络规模不变时对次可加性的模拟检验

从表2中可以清晰的反映出，当并购前后生产网络规模保持不变的情况下，即并购案例中完全剔除了由于规模经济原因而产生的并购协同效应，铁路并购案例仍然具有显著的协同效应。

表3是当并购前后生产网络的规模可变时的对铁路成本函数的次可加性模拟。

当网络规模可变时，铁路成本函数中的四个成本要素总共产生3281种向量组合，这意味着，共有705415种对次可加性的模拟检验。

表3的模拟检验中的多产品输出模型显示，在215起并购案例中，只有15%-17%的样本表现出严格的次可加性。在705415项模拟检验中，只有37%-38%的结果显示出并购后生产成本低于并购前生产成本。

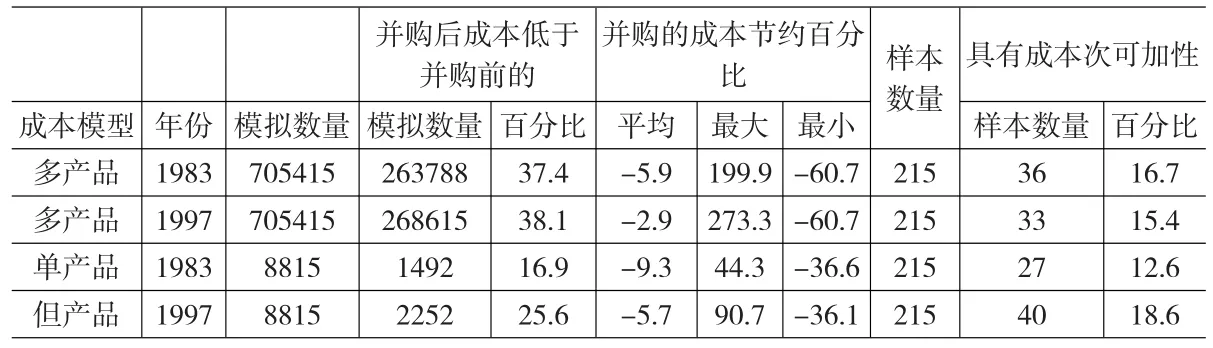
表3 网络规模可变时对次可加性的模拟检验

通过模拟检验不同的产品生产函数，并生产函数不再表现出次可加性时，企业规模达到临界值。使用1997年的成本结构做模拟检验，发现当铁路网络里程小于2500英里时，有98.8%的输出结果显示并购后的生产成本低于并购前的生产成本，生产函数具有次可加性。当铁路网络规模在2500英里至4700英里之间时，有80.2%的输出结果显示并购后的生产成本低于并购前的生产成本，生产函数具有次可加性。当铁路网络规模在4700英里至5700英里之间时，仅有20.8%的输出结果显示并购后的生产成本低于并购前的生产成本，生产函数具有次可加性。当铁路网络规模大于5700英里时，仅有1%的输出结果显示并购后的生产成本低于并购前的生产成本。

而模拟检验中，单产品成本模型和多产品成本模型存在差异。例如表3中所示，使用1997年的成本结构，单产品模型模拟检验中，有25.6%的检验结果显示并购后的生产成本低于并购前的生产成本，而多产品模型模拟检验中，这个比例是38.1%。

表4是2005年美国7家I级铁路公司的指标。在表4中可以看出，7家I级铁路公司中，北伯灵顿圣太菲铁路运输公司拥有的路网规模为51500英里；诺福克南方公司的路网规模为32000英里；CSX运输公司的路网规模为32000英里，联合太平洋铁路公司的路网规模为51742英里，GTC铁路公司的路网规模为10931英里，堪萨斯南方铁路公司的路网规模为6056英里，拥有路网规模最小的苏奥利涅铁路公司的里程为4238英里。

表4 2005年美国7家I级铁路公司的指标

7家I级铁路公司有6家铁路公司都处于并购形成的铁路公司生产成本反而高于并购前多个企业自行生产的生产成本。美国铁路公司的并购案例显示，虽然I级铁路公司的并购活动导致路网规模超过5700的临界值具有规模不经济效应，而并购协同效应更多的来自于铁路网络化整体运营所带来的运营协同。例如减少了铁路货物运输途中跨网络的交换成本，和在货物运输起点到终点间在并购后的网络内选择距离最短的连接路径而导致运输时间减少。

4 结论

本文通过对美国铁路超越对数成本函数检验和对铁路成本函数并购前后的次可加性检验，发现铁路网络具有临界值，当铁路网络达到临界值时，再展开并购活动，有99%的可能性会存在规模不经济现象。但是美国铁路的并购历史显示美国铁路网络演化的最终结果，即通过并购形成的7家I级铁路公司中6家，路网规模都超过了并购成本函数限定的路网规模临界值。这说明铁路公司的并购活动所获得的并购协同效应更多的是来自于铁路网络化运营所带来的网络运行协同，并且铁路公司并购后所获得的并购协同要大于超临界值规模进行并购而带来的规模不经济现象。客货分离后的中国铁路将产生迫切的重组需求。而美国铁路公司的并购实证分析将为中国铁路货运网络的并购重组提供决策参考。

[1]Class I Railroad Statistics.Association of American Railroads[Z].2010.

[2]Evans,D.S.,Heckman,J.J.A Test for Subadditivity of the Cost Function with and Application to the Bell System[J].American Economic Re⁃view,1984,74(4).

[3]John Bitzan.Railroad Cost Conditions—Implications for Policy,Pre⁃pared for th Federal Railroad Administration,U.S.Department of Transportation[Z].2000.

[4]Winston,C.,Corsi,T.,Grimm,C.,Evans,1.The Economic Effects of Sur⁃face Freight Deregulation[M].Washington,DC：Brookings Institution,1990.

[5]Friedaender,AF.,Spady,RH.Freight Transport Regulation；Equity,Ef⁃ficiency,and Competition in the Rail and Trucking Industries[J].Bell Journal of Economics,1980,8(2).