基于等级反应理论的民意类调查问卷选项策略

刘 全

（成都信息工程学院 统计学院，成都 610103）

1 问题提出

民意调查是使用科学的调查和分析方法，对某地方政府所管辖的居民的调查，通过调查了解公众的需求、行为特征、政策偏好及其对政府服务的评价，并确定公众对政府服务评价高低的决定因素，以利于政府改进服务的过程。

民意调查是对现行统计调查格局的突破，是对现行统计调查制度的重大创新和补充。我国统计工作受传统计划经济体制的影响，重心一直放在经济领域，而文化、社会领域的统计调查及研究始终处于从属地位，政治领域才刚刚起步。同时，我国民意调查的实践远远超前于理论的研究，这使得我国民意调查工作面临着诸多问题。综合国内民意调查研究，主要是对西方理论的介绍、我国民意调查实践工作的经验总结，而具有前瞻性、有针对性地对开展民意类调查理论研究，并有创新性成果的还鲜见。

民意调查的基本目的是了解公众对政府行为及其产生后果的评价，以及决定公众评价的影响因素。对政府行为和绩效的评价上，公众本着“合理的无知”原则，一般只能给出他们看得见、摸得着的政府施政行为及其结果的感知。所以，如何设计出科学的问卷（态度量表），能就公众对政府行为及其产生的后果进行准确地心理感知（如感受、意愿、态度等）调查是关键，其中，问卷中的问项选项、多级问项的选级、基于不同受访群体的问卷选项尤为重要。

项目反应理论（Item Response Theory,IRT）是心理学上对所谓潜在心理特质测量的一种科学理论，这与民意类调查研究目标一致。其中，等级反应理论（Graded Response Model,GRM）则是由Samejima(1969)发展起来的IRT模型的一种广义形式，R.Koch(1983)在他的研究中，首次证实了等级反应模型可应用与态度量表[1]。70年代起，GRM理论已在大多数国家成为心理测量学家的主要研究课题。近几年，国内学者漆树青、余嘉元、何晓群、柯惠新等在这方面进行了大量研究[2～4]，但其研究侧重于GRT在心理测评、标准化考试、试题库建设、自适应测验的应用等方面。

2 GRM模型研究

2.1 民意类调查问卷的GRM建模

根据IRT理论，若调查问项的备选答案只有正面（如满意，同意等）、负面（如不满意、不同意等）两种情形，并采用“0-1”记分法(正面为1，负面为0)时，则受访者对问项给出1（正面或积极）回答的概率可采用项目反应理论中的Logistic模型刻划。实际中常用二参数Logistic模型[1]（2PLM）：

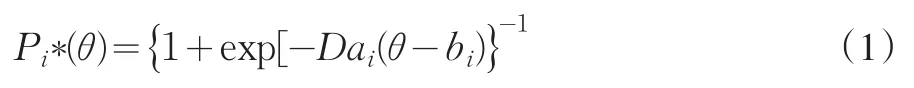
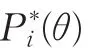
在民意类调查中，实际问项设计普遍采用Likert等级态度量表（如：3、5、7或9等级量表），其备选答案有多个等级（如：4=非常满意、3=满意、2=一般、1=不满意、0=很不满意，等等），为此，必须对“0-1”记分法的模型（1）进行扩展。

每条概率曲线表示受访者在问项i上评价为l等（l=0、1、2）及以上的概率。利用这种曲线，可得到态度量值为θ的受访者对问项i评价恰好为0（负面）、1（正面）的概率：

进一步，如果问项i共有ki个等级。则态度量值为θ的受访者给出评价为l（l=1，2,…,ki）等及以上的概率，不难由（1）式推广得到：

模型（3）便是普遍意义上的等级反应模型[5]，其函数图形称为等级项目特征曲线（Item characteristic curve，ICC），并都是（2）式中两条概率曲线之差。

2.2 基于GRM模型的调查问卷估计精度定义

通过问卷调查，获取受访者对某问项给出满意评价所对应的态度量值θ，实质是一个抽样推断过程。根据抽样理论，抽样推断的置信区间由抽样分布的标准误SE(θ)决定，其大小与估计精度成反比，为此，定义 I(θ)=1/SE(θ)2作为等级反应模型的估计精度是合理的，并称I(θ)为信息函数。

根据A.Birnbaum(1957)结论，问卷对受访者a的总信息量为各问项信息量之和[6]，即：

其中，m是问卷所含的问项数，Ii(θa)是问项i对态度量值为θ的受访者a的信息函数。在（3）式情况下，可以证明[7]：

信息函数Ii(θa)给出了问项i的基于不同态度量值θ受访者a的不同调查精度，或者说，Ii(θa)给出了问项i在态度量值为θ的受访者a上调查所能得到的信息量。

对态度量值为θ的受访者a，若已知各个问项所能提供的信息量Ii(θa)，则根据以上结论，显然有整个问卷对受访者a调查所产生的标准误：

显然，问项所能提供的调查信息量越大，则SE(θa)就越小，对受访者态度量值θ的估计就越精确，反之亦然。

3 基于GRM的问卷选项策略

3.1 基于目标信息曲线TIC的整体问卷选项策略

一个问项的信息量越大，则对整个调查的贡献越大；反之亦然。因而用问项信息函数值的大小来衡量问项的优劣显然是合理的。具体策略是：

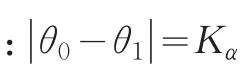
⑵计算各个备选问项的信息量，并按其信息量从大到小依此选取，直至信息量累计值刚好达到或超过TIC。关于备选问项信息量的计算，一般采用专门的等级项目反应软件，其计算过程是：先由（3）式得到各个备选问项的ICC曲线，然后根据（4）式计算出其问项的信息量。如某地关于“社会和谐度”民意调查问卷设计中，笔者采用Likert 5级态度量表编制出初始问卷（含39个问项），对该地区500位居民进行预调查，并经同向化处理，取得模型拟合的基础数据。若用户要求抽样标准误 SE(θ)在区间-1.0≤θ≤+1.0 内 不 大 于 0.4，则 由 公 式 ：I(θ)=1/SE(θ)2=1/0.42=6.25，表明问卷信息量累计值须大于或等于6.25。为此，利用以上500位居民的预调查数据，选用二参数逻辑斯蒂GRM模型（已对基础数据进行了单维性假定检验，检验结果表明符合GRM建模要求）。使用Multilog7.0软件得到相应的ICC曲线及各问项在-1.0和+1.0处的信息量Ii(θa)，再根据IRT要求去掉其中a≤0.3或a≥4，b＞2.95或者b＜-2.95 的项目，余下的24个问项依信息量从大到小排列（见表1）。

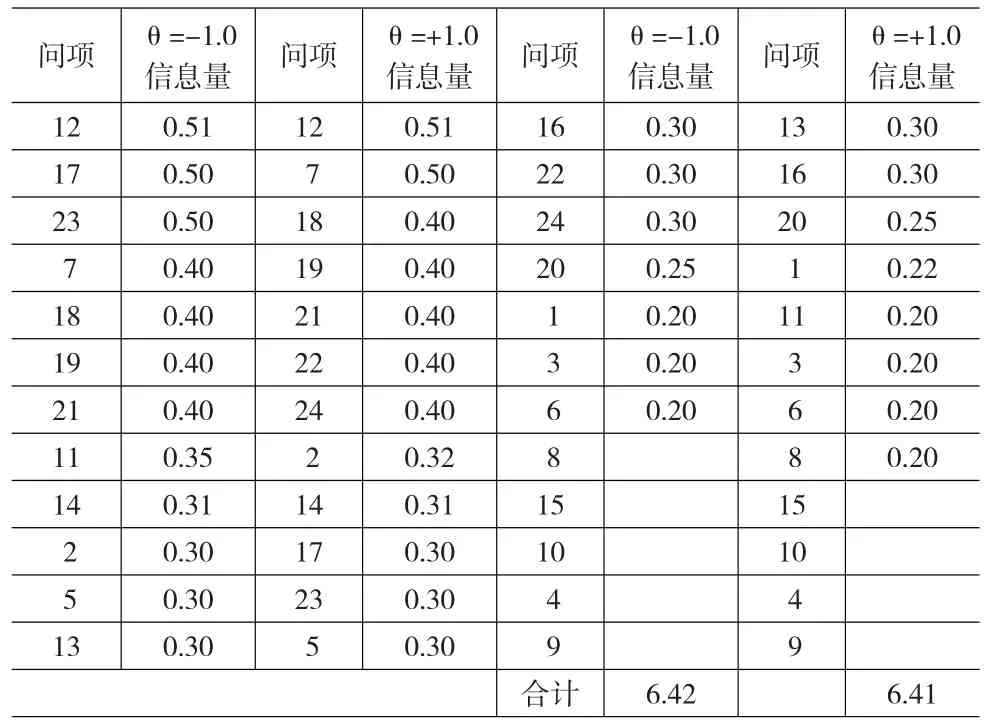
表1 各问项测量精度（信息量）排序

从表1按信息量大到小依次提取所需问项，直至满足最低累计信息量6.42的要求，从而得到满足调查误差要求的问卷方案（含20个问项）。

图1 某地“社会和谐度”民意调查问卷信息曲线

3.2 基于边际信度和拟合度的问项选级策略

选用多少等级（如3、5、7或9等）的量表是民意类调查中的另一个重要问题。由（3）和（4）式可知，问项的评价等级Ki对GRM的拟合度和评价精度有直接影响，换言之，选择合理的Ki可提高模型拟合度和调查评价精度。GRM在信息函数基础上，构建了边际信度（Marginal Reliability,MR）指标，MR反映了问卷的整体精度[8]，相当于经典测量理论中的信度系数α，其值越大越好。同时，GRM还采用似然比卡方统计量（-2Loglikelihood）进行模型-数据整体拟合检验[8]，其值越小越好。因此，问项等级的选择可通过考察其各种等级组合模式下GRM的精度和拟合度，选取最优等级组合模式而得到。

如“社会和谐度”问卷设计中，为了确定“您对该地区现时社会和谐程度评价”的备选项，从“非常不和谐”到“非常和谐”拟采用多少等级（如3、5、7或9）为宜。则在固定其它问项不变情况下，采用了对该问项按3、5、7或9等级分别设计，预调查取得数据后，选用二参数逻辑斯蒂GRM模型，使用Multilog7.0软件得分析结果（见表2），比较各等级下的MR、-2Loglikelihood值可知，该问项采用5等级评价最佳。

表2 “您对该地区现时社会和谐程度评价”各等级评价的统计量

另一方面，在民意调查中，当量表的备选等级设置较多（如5、7或9级）时，往往受访者容易出现趋中化或极端化的反应倾向，这种情况在前两级和后两级间最易发生，从而导致选择同一等级的受访者与其真实情况并不一致。为此，可将其量表的等级进行适当的合并。如在Likert 7等级量表中，可将第1、2等级，第6、7等级分别合并，即将7级评分改为5等级甚至3等级评分，则有可能使调查的精度和模型-数据拟合得到提高。

3.3 对不同受访群体的问卷选项策略

等级项目特征曲线ICC虽然刻划了受访者对问项各等级进行评价的概率，但是，对不同的受访者其刻划精度是不一样的，同样，对受访者团体的不同子体的适用性也是不一致的。比如，在社会和谐度调查中，可能存在问项i的等级特征曲线ICC适用于城市居民，但不太适用农村居民。换言之，问项i能很好地筛选出不同满意度的城市居民，但不能很好地筛选出不同满意度的农村居民情况。为此，问卷设计中，针对不同受访子体，基于等级反应曲线ICC，选择出更能准确评价出该子体态度量值θ的问项i，这对调查来说也是重要的。

如“社会和谐度”问卷设计中，考虑到城市、农村居民可能对问卷中的某些问项评价存在明显差异。为了选取分别适合城市、农村居民的调查问项，可就城市、农村不同受访群体，分析研究同一问项的等级项目特征曲线ICC在不同受访群体中的优劣，选出对该群体能更准确获得其态度量值的问项。

如“您对当前财富与分配满意度”问项的调查，一般来说，认可和谐度越高的受访者（不管是城市或农村受访者），圈填“4-满意、5-非常满意”的概率应更高，反之亦然。以下是该问项分别对城市、农村居民的项目特征曲线（图2、图3）：

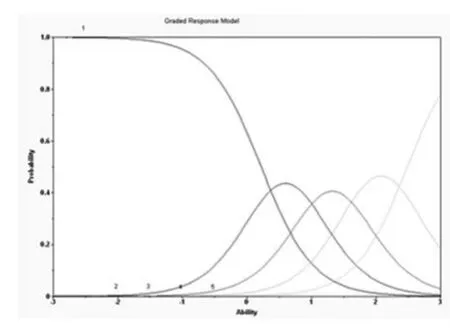
图2 问项四的项目特征曲线（城市）

图3 问项四的项目特征曲线

从图2可知，对当前财富与分配满意（特质区间[0，+3]）的城市居民评价中，圈填“4-满意、5-非常满意”评价等级的概率高，这符合实际情况。而从图3可知，对当前财富与分配满意（特质区间[0，+3]）的农村居民评价中，圈填“5-非常满意”评价等级的概率更高，这不太符合我国现阶段城乡差别的实际，说明该问项对农村受访者的态度量值测试质量低，即该问项不太适合农村受访者。

4 结论

本文构建了民意类调查问卷设计的等级反应理论模型GRM，研究了利用等级反应模型的信息函数评价问卷调查中的误差估计问题，提出了民意类调查问项的选项策略、多级问项的选级策略、基于不同受访群体的问卷选项策略等，一系列基于等级反应理论的民意类问卷设计技术问题，并结合某地开展的和谐社会调查讨论了具体实现过程。

实践表明，以上基于等级反应理论的民意类调查问卷选项策略具有严谨的科学性、很强的操作性。本方法允许调查方案设计者根据规定的调查精度，确定出目标信息曲线TIC，编制出符合调查精度要求的调查项目。同时，调查精度能在受访者满意度θ连续统上的若干点或区间得到严格控制。可见，本方法对民意类调查问卷设计质量提高具有重要的理论和实践意义。

[1]余嘉元.项目反应理论及其应用[M].南京：江苏教育出版社,1992.

[2]柯惠新,祝建华.传播统计学[M].北京：北京广播学院出版社，2003.

[3]漆书青.现代教育与心理测量学原理[M].北京：高等教育出版社,1998.

[4]许健,马世晔,何晓群.标准化试题的评价与IRT模型的应用[J].考试研究，2004,（8）.

[5]罗照盛等.项目反应理论等级反应模型项目信息量[J].心理学报,2008,40(11).

[6]涂冬波.信息函数在标准参照测验中的应用研究[J].江西师范大学学报,2005,（03）.

[7]周骏.等级反应模型下项目特征曲线等值法在大型考试中的应用[J].心理学报,2005,37(6).