线性回归模型几何分析：基于估计结果及检验统计量的考察

黄恒君，刘 明

（兰州商学院a.统计学院，b.甘肃省经济发展数量分析研究中心,兰州 730020）

0 引言

线性回归模型最基本的参数估计方法是普通最小二乘法，在最小二乘法下线性回归模型具有良好的统计性质，从数理的角度来分析，最小二乘估计方法及估计结果的数学特征也非常显著，用数学思想对最小二乘估计方法及估计结果进行分析和研究，能够将其直观化、系统化。我们曾利用正交和投影对普通最小二乘法原理作出了几何解释[1]，在此基础上，本文利用“长度”和“角度”等几何概念，分别对普通最小二乘估计形成的回归系数、相关系数、可决系数R2、F统计量作出几何分析，以期用数学语言表述它们，得到直观的、系统的分析结果。

1 长度、角度与相关系数

图1 长度与角度解释

由于-1≤cosθ≤1，-1≤r≤1，这就容易对相关系数作出解释。在坐标轴的第一象限，θ越接近于0，则正相关程度越高；在坐标轴第二象限，θ越接近于π，则负相关程度越高。特别地，当r=cosθ=0时，θ=π/2，此时，向量y与x相互垂直(正交)，即两者完全线性不相关；当r=cosθ=1时，θ=0，向量 y与x方向相同(平行或重合)，即两者完全线性正相关；当r=cosθ=-1时，θ=π，向量y与x方向相反(平行或重合)，即两者完全线性负相关。

上述二维欧氏空间的分析容易推广到n维。若x和y是n维欧氏空间中向量，其相关系数表现x和y在n维空间中的形成的两个点与原点形成的夹角，上述结论仍然成立。因此不难看出，相关系数就是cosθ。

2 线性回归模型的几何分析

2.1 回归系数的几何分析

考虑更一般的情形——把空间扩张成n维，x与y表现为n维欧氏空间中的两个向量，则有：

2.2 检验统计量的几何分析

根据上述相关系数的几何分析，并进一步结合图1，可以对可决系数作出几何解释。根据图1及勾股定理

由cos2θ的取值范围[0,1]，不难得到R2的取值范围为[0,1]。

同样可以对F检验作出几何解释。通过上述分析过程可知，回归方程总体显著性F检验可写为：

其中，df表示自由度。在样本量n和变量数K给定的情况下，df1/df2为常数，不妨设为A，因此

即F统计量是向量夹角的余切平方的线性函数。

3 多元线性回归模型的推广

3.1 多元推广

若样本容量为n，可设向量y、x1和x2来自n维欧氏空间，则x1和x2可生成n维欧氏空间的一个子空间(记为X)，在子空间X中，必然存在x1*与x2正交(如图2)。

图2 多元投影几何解释

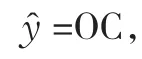
3.2 多元模型的一元分解

在多元线性回归模型中，如果解释变量之间相互正交，那么多元回归模型可以独立地分解为一元回归模型，即多元回归模型的回归系数估计结果与对应的单个解释变量与原被解释变量所构建的一元回归模型的回归系数估计结果相同。借鉴这一思路，我们对一般的情况进行分解，并由此说明多元线性回归模型的多重共线性问题。

同理，若先将y投影到x2方向，并进一步投影到x1，最终拟合结果以及残差相同，但中间分解过程不同。因此，在x1和x2非正交的一般情况下，多元回归不能独立地分解为一元回归。

若x1*与方向一致，即x1与x2正交，α=π/2，此时，B*、B和E三点重合，多元回归可独立分解为数个一元回归的情形。方差膨胀因子为1。当解释变量相互正交时，被解释变量对所有解释变量进行回归所得到的偏回归系数估计量分别与对单个解释变量回归时的系数估计量对应相等。

4 结语

由上述分析过程可以看出，普通最小二乘法的数学本质是将研究对象即被解释变量分解为相互正交的两部分。本文通过一元、二元线性回归模型，对普通最小二乘估计结果及检验统计量进行几何分析，发现参数估计结果、检验统计量等都可以在向量空间内用几何方法进行描述。该分析方法可以扩展到对多元线性回归模型的分析：最终表现为两个向量(被解释变量、解释变量线性组合)的长度和角度关系。

[1]刘明.普通最小二乘法的几何分析[J].统计与决策,2012,(4).

[2]庞浩.计量经济学[M].北京：科学出版社,2010.

[3]Kreyszig E.Introductory Functional Analysis with Applications[M].New York：John Wiley&Sons,1978.