一种求解扩展Bessel方程的边值问题的新方法——相似结构法

廖智健，李顺初

（1.北京大学元培学院，北京100871；2.西华大学应用数学研究所，四川成都610039）

0 引言

利用分离变量法去求解数学物理方程时，常常会遇到如下扩展的Bessel方程的边值问题［1－2］：

式中，A，B，C，D，E，F，G，H，a，b均为已知的实常数，且

文献［3－4］研究了标准型的Bessel方程的边值问题的解的相似结构，文献［5］研究了二阶常系数线性微分方程的边值问题的解的相似结构，文献［6－8］找出了相似结构的应用实例，文献［9－11］初步探讨了解的相似结构的适用范围，文献［12－15］进一步地指出了特殊的Bessel方程的边值问题解的相似结构在石油工程中的应用.从过去的研究中不难看出，边值问题（1）是相关应用的理论基础并具有较好的实用价值.本文通过适当的变量替换，引入引解函数，证实边值问题（1）的解具有相似结构，并提出了求解该类边值问题的一个新方法——相似构造法.

1 预备知识

引理1.1［1］若对边值问题（1）中定解方程作变量替换：

则可化为如下标准的Bessel方程：

式中，

引理1.2 边值问题（1）中定解方程的通解为

式中，C1，C2为任意常数；Jυ（·），Yυ（·）分別为υ阶的第一、第二类Bessel函数.

证明 因为Bessel方程（3）的通解［1，16］为

由变量替换式（2）知

引理1.3 若令

则有

证明 根据Bessel函数的微分性质

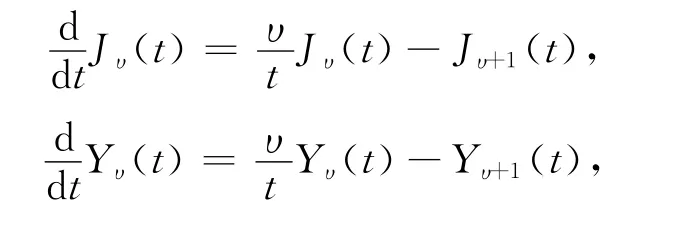
可以得到

同理可证式（8）～（10）成立.

引理1.4 若令

则有

这里，φi，j（x，ξ）（i，j＝0，1）为边值问题（1）的引解函数.

证明 根据定义式（11）及引理1.3可直接证得.

2 主要定理及其证明

先讨论边值问题（1）的右边界条件特殊的一种情形，它将是（1）的解的相似结构中的相似核函数.

定理2.1 若边值问题

（参数的限制与式（1）中相同）有唯一解，则其解为

证明 根据引理1.2知，式（15）中定解方程的通解为式（5），则

再由式（15）中的右边界条件［Gy＋Hy′］x＝b＝0知

由于边值问题（15）有唯一解，因而关于C1，C2的线性方程组（17）、（18）的系数行列式Δ≠0，且经计算化简和应用式（12）、式（14），得

求解线性方程组（17）、（18），得

将由式（20）、式（21）确定的C1，C2代入式（5）中，即得边值问题（15）的解：

再应用式（19）、式（11）、式（13），即得式（16）.

定理2.2 若边值问题（1）有唯一解，则其解为

证明 根据引理1.2知，式（1）中定解方程的通解为式（5），则由式（1）中的左边界条件

知

再由式（1）中的右边界条件［Gy＋Hy′］x＝b＝0，得到式（18）.

由边值问题（1）有唯一解知，关于C1，C2的线性方程组（18）、（23）的系数行列式Δ＊≠0，且经计算化简和应用式（12）、式（14），得

求解线性方程组（18）、（23），得

将由式（25）、式（26）确定的C1，C2代入式（5）中，即得边值问题（1）的解：

再应用式（11）、式（13）、式（24），并经整理后，即得式（22）.

由定理2.1和定理2.2，经观察或简易地运算，易得如下在实际应用中的几个有用的推论.

推论2.1 在边值问题（1）或（15）中，若右边界条件为y（b）＝0（即H＝0，G≠0），则相应的相似核函数

推论2.2 在边值问题（1）或（15）中，若右边界条件为y′（b）＝0（即G＝0，H≠0），则相应的相似核函数

推论2.3 边值问题（1）的解式（22）的结构中的第一个连分式有如下性质：

此式反映了解在左边界处的本质性的特征，在实际应用中起着十分重要的作用.

3 结论

（Ⅰ）由定理2.2知，解式（22）具有式相似性（称为解的相似结构式），即具有连分式乘积的形式并包含有一个相似核函数Φ（x），具有数的表现特征；且相似结构式中的系数仅与左边界条件有关，而与右边界条件及定解方程无关.

（Ⅱ）由定理2.1知，相似核函数Φ（x）是左边界为第二类边界条件下的解.相对于边值问题（1）来说，Φ（x）与左边界条件中的系数无关，仅与右边界条件及定解方程有关，是易于求得的.它表现为是相应边值问题的一种基础解.

（Ⅲ）由引理1.4及定理2.1知，只需由式（11）生成φ（x，ξ）（＝φ0，0（x，ξ）），即可求得相似核函数Φ（x）（它由φ（x，ξ）及关于第一、第二个变量分別求导后代入相应的值和右边界条件的系数而生成），而不必去求解边值问题（15）.

（Ⅳ）以上特征表明：只要先由φ（x，ξ）生成相似核函数Φ（x），再由相似结构式（22）进行组装，即可得到边值问题（1）的解.依此步骤获得边值问题的方法称为相似构造法.这无疑是解决微分方程的复杂边值问题的一个新思想和新方法.该方法有利于进一步地分析解的内在规律、解决相应的应用问题、方便编制相应的分析软件，它是微分方程理论的创新发展.

（References）

［1］Andrews G E，Askey R，Roy R.Special Functions［M］.Cambridge：Cambridge University Press，2000.

［2］Bleecker D，Csordas G.Basic Partial Differential Equations［M］.Boston：International Press Incorporated，1996.

［3］Jia Minhui，Li Shunchu.The similar structure of solution of differential equation on boundary value problem［J］.College Mathematies，2005，21（5）：37－39.贾闽惠，李顺初.Bessel方程的边值问题解的相似结构［J］.大学数学，2005，21（5）：37－39.

［4］Li Shunchu，Yi Liangzhong，Zheng Pengshe.The similar structure of differential equation on fixed solution problem［J］.Journal of Sichuan University（Natural Science Edition），2006，43（4）：933－934.李顺初，伊良忠，郑鹏社.微分方程定解问题解的相似结构［J］.四川大学学报（自然科学版），2006，43（4）：933－934.

［5］Li Shunchu.The similar structure of solution of second－order linear homogeneous differential equation with constant coefficients on the boundary value problem［J］.Journal of Xihua University（Natural Science Edition），2007，26（1）：84－85.李顺初.二阶常系数齐次线性微分方程边值问题的解的相似结构［J］.西华大学学报（自然科学版），2007，26（1）：84－85.

［6］Li Shunchu.Formal similarity of solutions to the class of 2－order partial differential equation in the Laplace space［J］.Journal of Xihua University（Natural Science Edition），2007，26（4）：83－86.李顺初.一类二阶偏微分方程的Laplace空间解的形式相似性［J］.西华大学学报（自然科学版），2007，26（4）：83－86.

［7］Li Shunchu，Zheng Pengshe，Zhang Yufei.The similar structure of pressure distribution in the composite reservoir［J］.Mathematics in Practice and Theory，2008，38（3）：23－28.李顺初，郑鹏社，张宇飞.复合油藏试井分析解的相似结构［J］.数学的实践与认识，2008，38（3）：23－28.

［8］Li Shunchu，Zheng Pengshe，Zhang Yufei.Similar strueture of pressure distribution in the multilayer reservoir［J］.Applied Mathematics A Journal of Chinese Universities（Ser A），2009，24（2）：234－238.李顺初，郑鹏社，张宇飞.合采油藏试井分析解的相似结构［J］.高校应用数学学报，2009，24（2）：234－238.

［9］Li Shunchu.The similar structure of solutions to the boundary value problem for second－order linear homogeneous differential equation［J］.Journal of Xihua University（Natural Science Edition），2009，28（5）：40－41.李顺初.二阶齐次线性微分方程的边值问题的解的相似结构［J］.西华大学学报（自然科学版），2009，28（5）：40－41.

［10］Li Shunchu.Preliminary exploration and prospects of the similar structure of solutions of differential equations［J］.Journal of Xihua University（Natural Science Edition），2010，29（2）：223－226.李顺初.微分方程解的相似结构的初探与展望［J］.西华大学学报（自然科学版），2010，29（2）：223－226.

［11］Wang Junchao，Li Shunchu.The similar structure of solutions of second－order linear homogeneous differential equation［J］.Pure Mathematics，2012，2（1）：23－27.王俊超，李顺初.二阶齐次线性微分方程解的相似结构［J］.理论数学，2012，2（1）：23－27.

［12］Sheng Cuicui，Li Shunchu，Guo Lijie.Similar structure of solutions for spherical flow homogeneous fractal oil pool［J］.Journal of Lanzhou University of Technology，2011，37（6）：136－139.盛翠翠，李顺初，郭丽洁.分形均质球向流油藏的解的相似结构［J］.兰州理工大学学报，2011，37（6）：136－139.

［13］Guo Lijie，Li Shunchu，Sheng Cuicui.Similar structure of solutions for radial flow of fractal reservoir［J］.Fault－Block Oil ＆Gas Field，2012，19（1）：114－116.郭丽洁，李顺初，盛翠翠.分形油藏径向渗流问题解的相似结构［J］.断块油气田，2012，19（1）：114－116.

［14］Li Shunchu，Li Wei，Li Xiaoping，et al.The construction method for solving radial flow problem through the homogeneous reservoir［J］.Applied Mathematics，2012，3（6）：517－522.

［15］Sheng Cuicui，Li Shunchu，Li Quanyong.Effective wellhole radius model for fractal reservoir with spherical flow and its similar structure of solution［J］.Journal of Harbin University of Science and Technology，2012，17（3）：37－41.盛翠翠，李顺初，李全勇，等.分形球向流有效井径模型及其解的相似结构［J］.哈尔滨理工大学学报，2012，17（3）：37－41.

［16］李顺初，黄炳光.Laplace变换与Bessel函数及试井分析理论基础［M］.北京：石油工业出版社，2000.