预应力混凝土结构中考虑徐变的挠度计算实用方法
张振华
(北京市城市道路养护管理中心,北京100069)
1 前言
预应力混凝土结构指在其中预先建立起内应力的混凝土结构,这种应力的大小和分布能够抵消或部分抵消来自外界的荷载引起的应力,在混凝土结构中得到广泛应用,特别是在大跨度结构中具有优势。其中徐变是其中一个重要因素[1-2]。本文通过实例对考虑徐变的两种挠度计算方法—分离法和弯矩图法进行介绍,有利于这两种简便快捷的计算方法的推广应用[3-5]。
在钢筋混凝土构件中,预应力一般是靠张拉预应力筋来实现的。同时也存在其它的建立预应力的方法。
目前,人们普遍认可了三种不同的概念来说明和分析这种预应力混凝土形式的基本行为。
第一种:预加应力能使混凝土在使用状态下变脆性材料混凝土为弹塑性材料。
第二种:预加应力使高强度钢筋和混凝土有效的结合,同时发挥二者的优势。
第三种:预加应力实现了和外荷载的平衡。
这三种概念从不同角度解释了预应力混凝土的原理。第一种概念指出了预应力混凝土的主要工作状态;第二种概念反映了预加应力对发挥高强钢材和混凝土潜力的必要性;第三种概念则揭示了预加力和外荷载效应的相互关系。
2 计算反挠度或挠度的两种方法
2.1 计算反挠度或挠度的第一种方法——分离法
本法是取混凝土作为分离体,把它和力筋分离,并用一组作用于混凝土上的力来取代力筋,如图1所示。两端锚固处作用一对对称分力,力筋在混凝土中每个转弯处将产生横向力或辐向力。在这里为了简便计算,通常做以下假定:

图1 由预应力引起的挠度计算
1)在计算惯性矩时,可以用混凝土的毛截面来代替净截面。
2)产生挠度的预加力值是介于初始和最终有效预应力之间的某个数值,根据经验选取一合理数值就可保证计算的准确性。
3)假定沿梁轴线方向的预应力分力是不变的,但力筋倾斜角度较大时除外。垂直于梁的预应力横向分力则按预应力乘弯转角的正切来计算,但角度过大时除外。
4)假定预应力的横向分力在力筋急转弯处为集中力,而在力筋转弯平缓处则为沿弯道均匀分布的。
5)各种计算都可以依据预应力筋的重心轴把所有的力筋作为一个整体来处理而不予分别计算。
6)在常见尺寸的预应力梁中,剪切挠度不大,可以忽略不计。
2.2 计算反挠度或挠度的第二种方法—弯矩图法
该方法也是依据上述假定,但不用计算力筋对混凝土的作用,而是依据力筋的重心轴的形状直接给出力筋所产生的弯矩图。在静定梁中,弯矩图与力筋重心轴的偏心形状相类似,因而只要利用另外一种比例尺寸来绘偏心形状就得出弯矩图,从而利用初等材料力学算出挠度。但是,在超静定结构中,为了得出较精确的解,就要进行修正,这是因为预应力所引起的赘余反力会产生力矩,从而引起挠度的变化。
2.3 考虑梁体自重的挠度
梁体自重将依据支撑条件产生挠度,这种挠度可以用通常的弹性理论来计算。把预应力和梁自重产生的挠度值代数相加,就得出预应力传递时梁的总挠度值。
2.4 挠度的修正
以上介绍的是初始挠度,事实上,梁经过一段时间之后,挠度会发生变化。首先是预应力的损失会减少挠度,其次是徐变的作用会增加挠度。
3 利用上述方法进行计算的实例分析
例:如图2所示一跨度为10m的预应力混凝土梁,采用断面为780mm2高强度钢丝,并用后张法施加预应力,刚加力后的瞬时初始应力为960MPa,设Ec为28000MPa,求跨中处预应力和梁自重所产生,并估算一个半月之后的挠度。假定徐变系数Cc徐变=1.8,该时的有效预应力为830MPa。
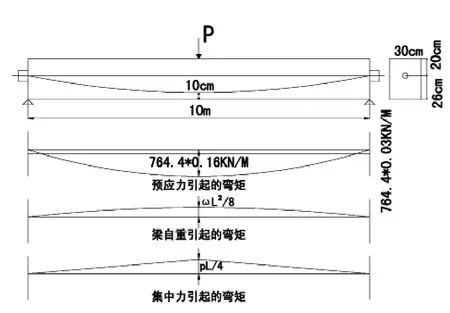
图2 预应力混凝土梁计算实例图
3.1 采用第一种方法计算
取混凝土作为分离体,并用一组作用在混凝土上的力来代替预应力筋,即用集度为
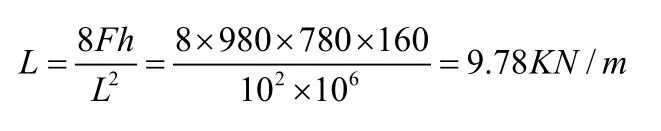
沿梁长度方向均匀分布的荷载来取代中央矢高为16cm的抛物线力筋。另外,在梁的两端偏上部分别作用一偏心荷载,每个荷载产生764.4×0.03=22.932KN·m的弯矩。梁的自重W = 1×0.3×0.46×26= 3.588KN/m, 因 此作用于混凝土的净均布荷载为9.78-3.588=6.192KN/m。用下列普通挠度公式可以算出净荷载在跨中所引起的向上的挠度为:
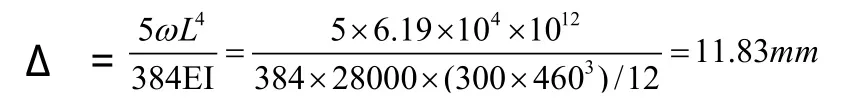
下面计算两端弯矩所引起的向下的挠度为:
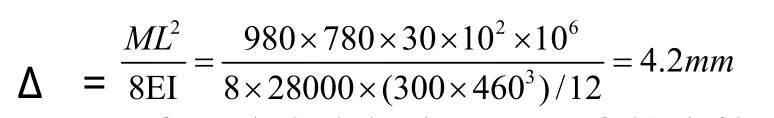
于是,由预应力和梁自重所产生的净挠度为:
11.83 -4 .2 =7.63mm向上的反挠度。
3.2 采用第二种方法计算
依据力矩的偏心曲线,绘出弯矩图,见图2,应用弯矩-面积原理,计算预应力引起的向上的挠度为:
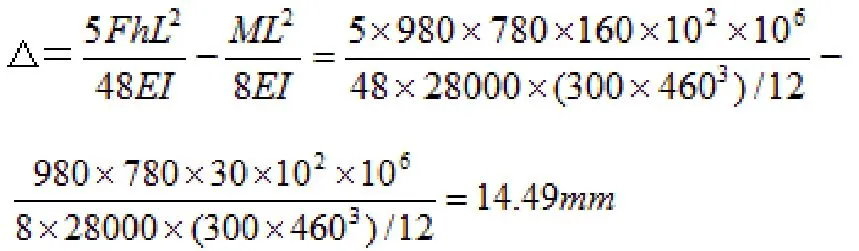
梁的自重所引起的向下的挠度为:
两种方法计算结果完全相同。
3.3 挠度的修正
由于预应力从960MPa减少到830MPa,因而预应力所引起的挠度可以用系数830/960来修正。徐变系数为1.8,可以用系数1.8来增加徐变引起的挠度。因此,在无外荷载作用时,经过一个半月的最终挠度可以估算为:
(14.49×830/960-6.86)×1.8 = 10.2mm
向上的反挠度。

4 结语
预应力混凝土梁在开裂之前的挠度能够预测得比钢筋混凝土梁更为精确。本文所提到的两种计算挠度的方法,在设计与分析预应力混凝土结构时带来了极大的方便,它具体形象化地帮助我们观察到随着时间过程而变化的挠度,表现出很大的优越性,无论在计算分析方面或是在形象地认识问题方面都表现出它的特点,因而值得大为推广。通过上述实例,我们也可以看到,利用上述两种方法来分析预应力混凝土结构挠度是比较容易和方便的,同时人们对问题的理解程度也大大提高,对提高设计能力提供了平台。
[1]刘徳辉.基于有效惯性矩的预应力混凝土梁的挠度计算[J].山西建筑,2008,35(34):81-82.
[2]宋郁民,刘媛,周世军.预应力混凝土桥梁悬臂施工中徐变挠度的计算[J].2008,4(27):25-28.
[3]贺拴海.桥梁结构理论与计算方法.人民交通出版社[M],2003.
[4]李国平.桥梁预应力混凝土技术及设计原理[M].人民交通出版社,2004.
[5]过镇海,时旭东.钢筋混凝土原理和分析。清华大学出版社,2003.作者简介:

