基于流固热耦合的1000MW级汽轮发电机滑动轴承性能分析

张培良，张 宏，武中德，刘 琪

（水力发电设备国家重点实验室，哈尔滨 150040）

前言

机组的稳定运行是至关重要的，轴承是决定轴系稳定性优劣的关键部件，选择一个合适的轴承型式和合理的结构参数对轴承的静态特性和动态特性关系极大。100～300MW和1000MW汽轮发电机径向轴承现在普遍采用圆或椭圆轴承，600MW汽轮发电机径向轴承采用混合瓦轴承，已具有20年的发展和运行经验。1000MW 汽端发电机径向轴承采用下瓦开沟的圆柱瓦轴承，励磁机采用4瓦可倾瓦轴承。特别是下瓦开沟的圆柱瓦轴承与我国的汽轮发电机径向轴承结构不同。

下瓦开沟的圆柱瓦轴承在实际工作运行中的润滑承载机理至今还不大清楚，本文主要目的是揭示该种径向滑动轴承的运行机理。轴承结构型式一般是根据给定条件，参照同类型机组中轴承结构型式和相应轴承的特性选定。大体上可以认为：圆柱轴承适用于较低的速度和较大的载荷，椭圆轴承适用于较高的速度和中等的载荷，椭圆度大的椭圆轴承和可倾瓦轴承适用于较高的速度。国内外汽轮发电机制造厂家对大型机组的轴承选型是比较慎重的，对于大型机组，国外多数厂家采用工艺复杂但稳定性好的瓦块式轴承，国内厂家多采用制造简单的椭圆轴承。主要是国外机组的额定转速多为3600r/min，而国内机组的额定转速为3000r/min。轴承稳定运行转速低于国外。1000MW核电发电机转速1500 r/min，轴承采用圆柱瓦，有利于提高承载能力。

国内外学者大多利用求解雷诺方程的方法研究滑动轴承性能，这种方法具有计算时间短的突出优点。近年来，人们开始通过 CFD和 FSI的方法直接求解N-S方程的方法研究轴承性能，这种方法可以考虑任意复杂结构型式的轴承。但目前应用CFD和FSI的研究方法均没有考虑温度对粘度、温度对密度等因素对轴承性能的影响。

本文对上下瓦开沟的圆柱瓦轴承建立了三维计算模型，采用流体-固体-热三场耦合的方法（TFSI）比较了 TFSI方法和 Reynold方法的计算结果，研究了1000MW及1400MW级汽轮发电机径向轴承的上、下瓦开槽对轴承性能的影响。

1 控制方程

1.1 流体域控制方程

滑动轴承中润滑油的流动情况可以用一下控制方程来描述：

（1）连续性方程

ρ为密度，v为速度矢量。

（2）动量守恒方程:

式中,

τ为应力张量形式如下:

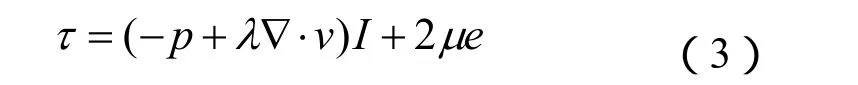
p是流体微元体上的压力，λ是体积粘度系数，μ为动力粘度，I为单位张量，e为应变速率张量，

（3）能量方程

式中，是体积矢量，∇是拉氏算子，q是热流密度。

1.2 固体热传导方程

固体内的热传导方程为：

T是温度，qB生热率，kx，ky，kz是热传导率：

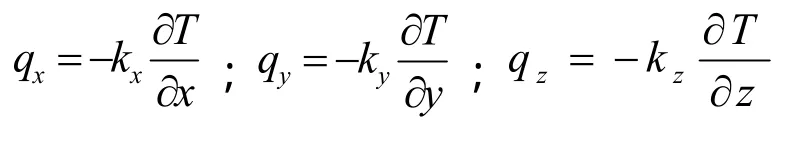
qx，qy，qz是热流密度。

1.3 固体热弹变形方程

按位移求解的分析过程最终归结为解平衡方程组：

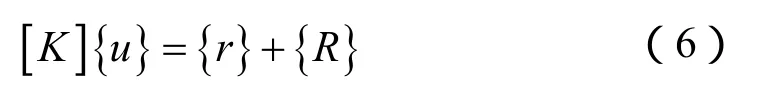
［K］是刚度矩阵，{u}是节点位移列阵，{r}是节点载荷列阵，{R}是变温等效载荷列阵。

2 轴承结构特点及有限元模型

发电机转子由2个圆柱瓦轴承支撑，结构见图1。上瓦开沟可有效冷却轴承并降低摩擦损耗，下瓦开有周向的中心槽（宽度40mm），HEC已设计生产的大型汽轮发电机轴承还没有采用过。为了保证轴的灵活，避免由于轴的偏斜或同轴度偏差而产生的应力集中，轴瓦采用球面支撑。汽端载荷较大，所以计算按汽端轴承计算。

图1 轴承结构

1000MW 级汽端轴承直径D=750mm，直径间隙C=1.5mm，长径比L/D=1.2，负荷1053KN，供油温度46℃，转速 1500r/min；1400MW 级汽端轴承直径D=800，直径间隙C=1.6mm,长径比L/D=1.025，负荷1222.6kN，供油温度46℃，转速1500r/min，供油压力0.05Mpa。

模型包括上下瓦油沟，巴氏合金层，轴承座，轴领以及进油口。由于油膜厚度很小，使用六面体单元的结构化网格，图2为模型整体网格，左侧为油膜，右侧为轴承座和轴。压力速度耦合采用SIMPLEC算法。动量、能量采用二阶迎风离散格式进行模拟计算，模拟精度为1×10-4。网格总数为32万。

边界条件：轴承座外表面自由度固定。油膜外表面与轴瓦、油膜内表面与轴颈为流固耦合界面，其相对速度为0，且轴瓦与外油膜速度为0。油膜通过流固耦合界面与轴承座和轴进行换热。油膜轴向出油口压力与外界压力相等，且认为径向压力梯度为 0，轴承外圆表面及其两端面和轴颈两端面及其非轴承段外圆表面，设温度为一常数，t=46℃。

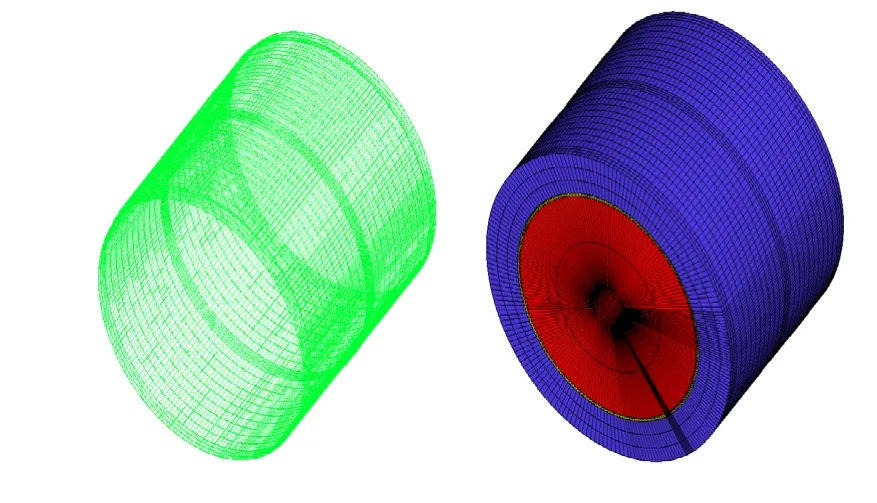
图2 模型网格

3 计算结果及分析

3.1 油膜压力分析

内油膜压力分布如图4，参照表1发现1000MW级汽端轴承油膜压力比较已有常规软件，计算结果较小，主要原因是耦合计算考虑的轴瓦在动压作用下会下凹变形，改变油膜分布和峰值大小，而 Reynold方法没有考虑轴承座的变形。1400MW 级汽端轴承的压力峰值与 Reynold方法基本一致。普通圆轴承在与动压成180°的方位会形成负压区，且面积与动压区面积基本相等，但从图4可见负压基本集中在上瓦油沟的末端，因为此轴承开有上油沟。负压会使润滑油产生空化现象，负压增大则气化增加，使得油的混合密度下降，不利于油膜承载，上瓦开油沟的方式有效转移并减小了空化范围和程度。

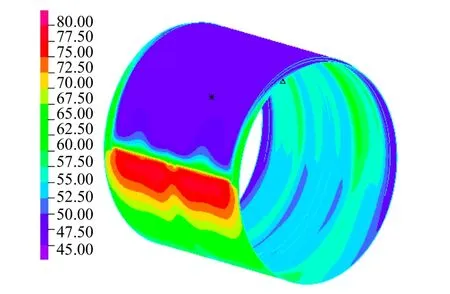
图3 1000MW汽端轴承油膜温度分布（单位：℃）

3.2 温度分析

1000MW级汽端轴承油膜温度计算结果和瓦面温度计算结果对比结果见表1。计算考虑了的进油量和进油温度对轴承温度的影响。由图3可见，最高温度分布不在油膜压力最高的地方，而是与油膜压力分布成一定相角，且由于宽度40mm的下油沟的影响，增加了油沟所在位置的周向油量，有效带走了油膜热量，降低了油膜温度，使油膜中部温度分布明显降低。油膜温度的降低会增加润滑油粘度，增加承载能力和油膜厚度。可见含有下油沟的结构显著提升了径向轴承的润滑性能。对比图 3和图 5，油膜与轴瓦的最高温度一致，即油膜温度等于轴瓦表面温度，与常规计算软件的计算结果相近，相互佐证了两种计算方法的合理和可靠性。

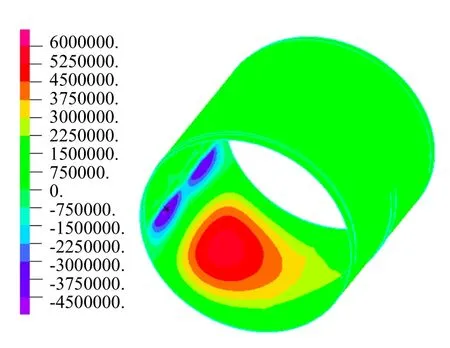
图4 1000MW汽端轴承油膜压力分布（单位：Pa）

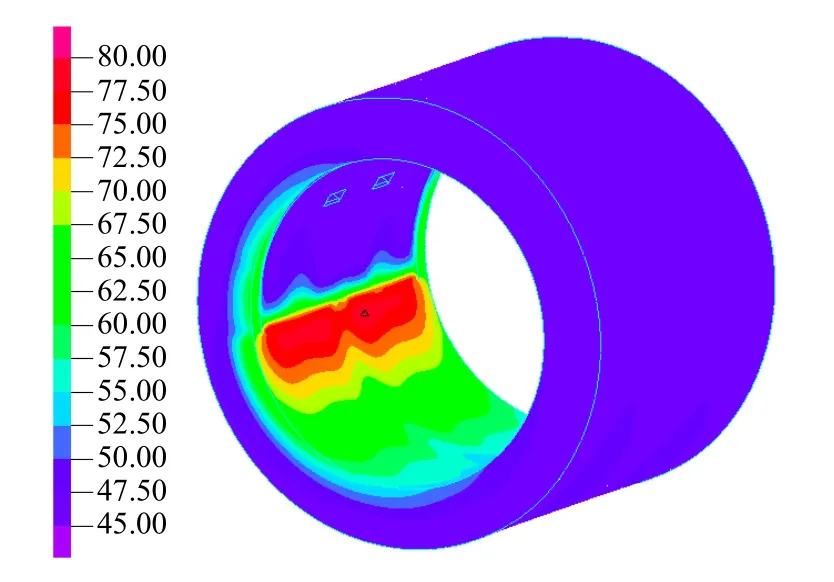
图5 1000MW汽端轴承座（含巴士合金层）温度分布（单位：℃）

图6 1000MW汽端轴承座（含巴士合金层）变形分布（单位：m）

3.3 变形分析

因为轴承的热分布和压力分布不在相同的相位，在热量的作用下，轴瓦有向外热涨的趋势；在油膜压力的作用下轴瓦有向下凹，形成油兜的趋势。在两者的相互作用下，轴承整体变形趋势如图 6，变形在轴瓦表面沿周向呈大字型分布。轴瓦边缘变形最大，是由轴瓦材料热涨后有被挤出的趋势造成的，与油膜温度分布相对应的是，轴瓦在高温区域变形相对较大。

3.4 计算结果对比

本文计算了1000MW汽端轴承和1400MW汽端轴承两种结构的径向轴承，与基于解 Reynold方程的轴承计算软件的计算结果和厂家给出的温度数据进行了对比。对比表1的1000MW汽端轴承结果，流固热耦合计算结果较常规计算方法计算温度较高，但低于厂家提供温度数据，温差为 1.6℃。对于 1400MW 汽端轴承计算参数，二者相差不大，温度差 2℃。无论是1000MW还是1400MW汽端轴承，其油膜厚度较常规计算方法的计算结果略小。

表1 1000MW汽端轴承计算结果对比

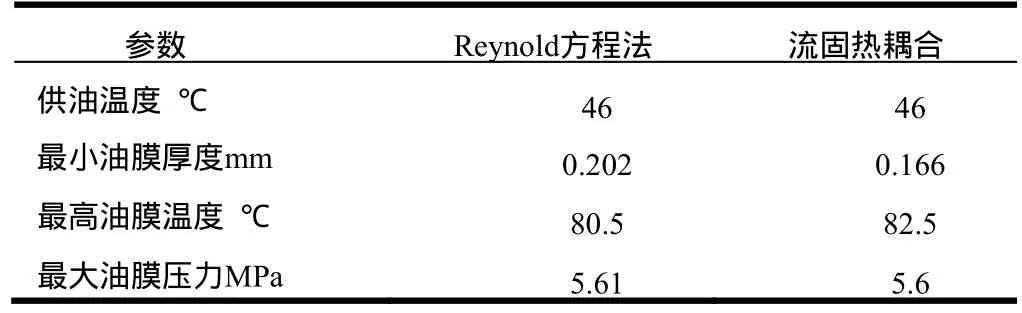
表2 1400MW汽端轴承计算结果对比

4 结论

（1）本文利用CFD-TFSI方法（采用流体、固体、热三场耦合方法），对1000M汽端轴承及1400MW汽端轴承进行分析。特别是下瓦中心沟的影响清晰可见。直观反映油膜厚度、压力及温度分布。轴承座温度分布图，变形分布图，形象直观。

（2）流固热耦合分析结果与基于二维雷诺方程的差分计算方法计算得到的结果基本吻合，后者在工程方实践方面有广泛的成功应用背景，证明了流固热耦合方法在工程应用上的的可行性。

（3）从分析结果上看，轴承上油沟改变了空穴产生的位置和程度；下油沟改变了温度分布，一定程度上减小了有效承载面积，增加了油膜强度及稳定性。

[1]张直明. 滑动轴承的流体动力润滑理论[M]. 高等教育出版社, 1986.

[2]F.T.巴威尔. 轴承系统—理论和实践[M]. 机械工业出版社, 1983.

[3]平克斯 O, 斯德因李希特 B.. 流体动力润滑理论[M]. 机械工业出版社, 1980.

[4]岳戈, 陈权, 等. ADINA应用基础与实例详解. 人民交通出版社, 2008.