敏感性问题随机化抽样调查方法浅析

李 健

（内蒙古化工职业学院，内蒙古 呼和浩特 010010）

敏感性问题是指所调查的内容涉及私人隐私而不愿或不便于公开表态或陈述的问题.例如学生在考试中有作弊现象，青少年的婚前性行为，社会上的卖淫嫖娼、赌博吸毒、偷税漏税等问题都是这一类问题，对这些问题的调查就是敏感性调查.

对于敏感性调查，如果直接提问，被调查者往往会拒绝回答，或不提供真实情况，因此对这一类调查必须采用经过特别设计的调查方法，以消除被调查者的顾虑，使它们能够如实回答问题.这种为敏感性问题调查特别设计的技术即是随机化回答技术，其基本特征是被调查者对所调查的问题采取随机回答的方式，避免在没有任何保护的情况下直接回答敏感性问题，从而既对被调查者的隐私和秘密加以保护，且能获得所需的真实资料.

敏感性问题按问题指标特征可分成属性特征问题和数量特征问题两类.本文将按这两类介绍一些已有的随机化调查模型.

为了得到敏感性问题的可靠的样本数据，使被调查者能够很好地配合调查.Warner在1965年开创性地提出了随机化回答调查法，这种调查方法的原理是在调查中引入随机化装置，使被调查者在保证真实回答的前提下，采用随机化回答装置，既能为被调查者保护个人隐私，也能使调查者获得所需的真实信息.之后，又出现了各种敏感问题调查方法.

1 定性敏感性问题随机化调查方法的发展状况

Waner1965年首先引入了敏感性问题的随机化调查方法，揭开了随机化调查的序幕.之后Simmons(1967)、Mangat(1990,1994)、Kuk(1990)、Singh(2002)等一些学者进一步发展了随机化回答技术.这些学者提出的调查方法解决的是定性敏感性问题的调查，即估计总体中具有敏感特征个体所占的比例.

1.1 Warner随机化模型（又称相关问题模型）

其设计原则是根据敏感性特征设计两个相互对立的问题，“你有敏感属性A吗？”和该问题的对立问题“你没有敏感属性A吗？”让被调查者按预定的概率从中选一个回答，调查者无权过问被调查者究竟回答的是哪一个问题.

根据矩思想得到πA的一个无偏估计量为：

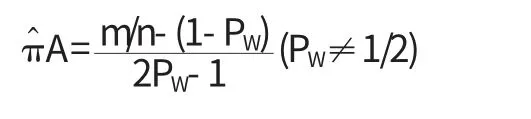
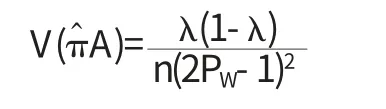
其中λ=πAPW(1-πA)(1-PW)为被调查者回答“是”的概率.

1.2 Simmons随机化模型（又称无关问题模型）

Simmons于1967年对Warner模型作了改进.其设计仍是基于Warner的随机化回答思想.在设计调查方案时，用无关的问题Y代替了Warner模型中的敏感性问题A的对立问题.如Y为“你是四月出生的吗?”,“你喜欢蓝色吗？”等等.

πA的一个无偏估计量为：

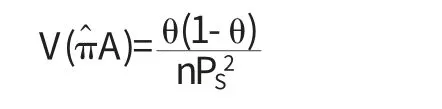
其中θ=πAPS+πy(1-PS)为被调查者回答“是”的概率.

1.3 Mangat 1990随机化回答模型

Mangat（1990）提出一个具有两个随机化装置的方法.第一个装置由两条陈述组成，即（i）“我有敏感属性A”，（ii）“到第二个装置”，配置概率分别为T和1-T.第二个装置和Warner装置完全相同具有设计参数PM和1-PM.

πA的一个无偏估计量为：

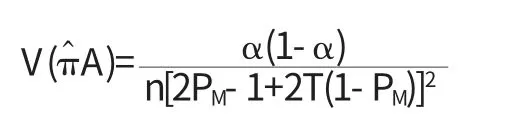
其中α=TπA)1-T)[πAPM+(1-πA)(1-PM)].

1.4 Mangat 1994随机化回答模型

这个装置是Mangat在他1990年提出的方法的基础上将随机化装置进一步进行简化而得出的，它使得被调查者的回答更为简便.

πA的一个无偏估计量为：

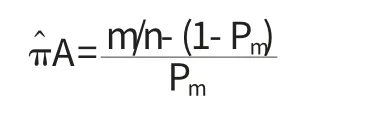
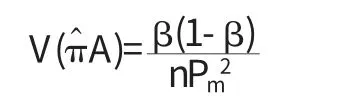
其中β=πA+(1-πA)(1-Pm).

1.5 KUK随机化装置

此装置的特点是不要求个体给出一个“是”或“否”的回答，调查方法为：个体分别根据参数θ1和θ2的两个Bernoulli分布产生两个结果.如果他或她有敏感属性A，要求个体回答第一个结果.如果他或她没有敏感属性A，则回答第二个结果.

πA的一个无偏估计量为：

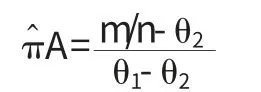
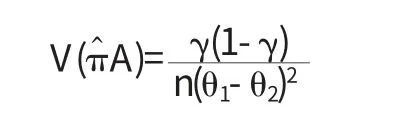
其中γ=πAθ1+(1-πA)θ2为样本个体报告“第一个结果”的概率.

2 定量特征敏感性问题随机化调查方法的发展状况

使用简单随机有放回抽样方法从N个总体中抽取n个简单随机样本.所要解决的问题是估计总体中敏感问题特征量X的均值

对于定量敏感性问题的研究，Greenberg(1969,1971)、Eichhorn和Hayre(1983)、Gupta(2002)、Bar_Lev(2004)等提出了一些可供选择的随机化调查方法.Gjestvan等人2007年提出了在效率上优于Bar-Lev(2004)模型的强迫回答模型.

设X表示对定量敏感问题的回答值，S表示一个与X相互独立的正的随机数，且S的均值与方差已知，分别记为θ,γ2.回答者所产生的回答是敏感变量X与随机数S的乘积.调查者最终收集到的是个体关于敏感指标的扰动回答Z=XS.样本中的每一个个体使用某种随机化装置产生一个随机数S，调查者不知道被调查者产生的随机数S.这里随机数S被EH称为扰动随机变量.使用简单随机有放回抽样(SRSWR)方法从总量为N的总体中抽取容量为n的样本，则样本中的第i个个体报告的回答值为zi=xisi,样本均值为

2.1 Greenberg模型(RG)

调查方法如下：

(1)产生一概率密度为f(y)的随机数Y.

(2)产生一0—1分布的随机数ε，且P(ε=1)=PG.

(3)若ε=1，则被调查者直接回答敏感性问题X；否则要求被调查者回答看到的Y值.

X,Y,ε 相互独立.研究者只能看到被调查者给出的最终回答zi.

将之归为模型，则得：

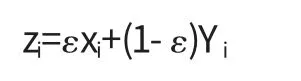
X均值的无偏估计量为:

估计量XG的方差为：

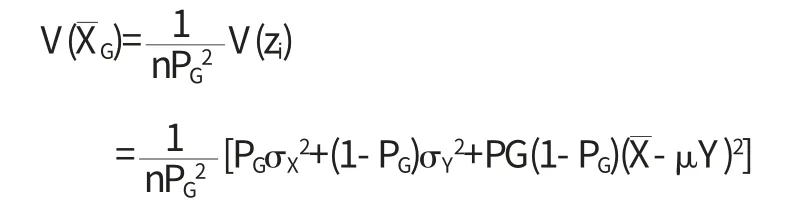
2.2 Eichhorn和Hayre模型

Eichhorn和Hayre(1983)对总体的敏感指标X的均值μx给出一个如下的无偏估计量

方差为

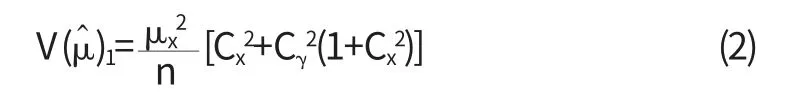
其中σX2=V(X)，Cx=σx/μx,Cγ=γ/θ,而Cx=σx/μx,Cγ=γ/θ 分别表示总体敏感指标X和扰动变量S的变异系数.

2.3 Gupta扰动变量回答模型

2002年Gupta等人在Eichhorn和Hayre(1983)扰动回答模型的基础上给出一种可选择的随机化调查技术，在此模型下，每个个体选择如下两类问题中的一类：

(a)回答者报告敏感指标真值X,

(b)回答者报告扰动回答XS,其中S为事先产生的与相互独立的扰动随机数.且满足E(S)=θ=1.调查者收集到的关于敏感指标X的扰动回答是Z=XSW,其中W为示性随机变量，即，令P0为个体报告扰动回答的概率，则E（W）=P0.调查者根据所调查问题的敏感程度来选择设计参数P0的值.如果所调查的问题较为敏感，此时人们倾向于使用扰动回答，则调查者会选择一个较大的P0值.如果问题是非常不敏感的，此时人们倾向于作直接回答，则调查者会选择一个很小的设计参数P0.容量为n的简单随机有放回样本(SRSWR)中的第i个个体报告的回答值为

Gupta(2002)给出的对μx的一个无偏估计量为

方差为

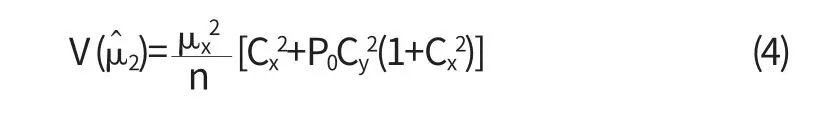
2.4 Bar-Lev,Bobovitch和Boukai扰动变量回答模型

Bar-Lev,Bobovitch和Boukai2004年给出一种改进的扰动回答模型，设X是所要调查的定量敏感指标，Y是一个分布已知的扰动随机变量，X与Y相互独立，P0是调查装置设计参数.

被调查者遵循如下的随机化回答原则：Z=XSW其中W为示性随机变量，即，令P0为个体报告扰动回答的概率，则E（W）=P0.其中E(S)=θ,V(S)=γ2为已知.使用简单随机有放回抽样(SRSWR)的方法从容量为N的总体中抽取容量为n的简单随机样本，样本中n个个体给出的随机化回答值为等给出的敏感指标均值的无偏估计量为

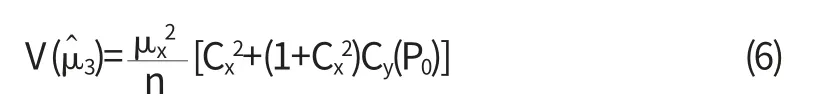
2.5 Gjestvang和Singh强迫回答模型

在Gjestvang等人提出的强迫回答模型中，随机化调查装置设计如下：一个装有红黄蓝三种颜色卡片的箱子，箱中三种颜色卡片所占的比例分别为p1,p2,p3，且满足条件p1+p2+p3=1，每一张卡片上都印有一个确定的数值，这个数值是由调查者设定的.在调查者不在场的前提下，每一个简单随机样本个体随机从箱子中抽出一张卡片，如果卡片的颜色是红色的，则要求个体报告敏感指标X的真值；如果卡片的颜色是黄色的，则要求个体报告敏感指标与扰动变量的乘积值XY；如果卡片是蓝色的，则要求个体报告印在卡片上的数值F.个体作出回答的分布为

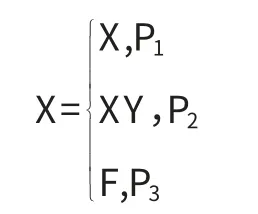
强迫回答模型下，敏感指标均值的一个无偏估计量为

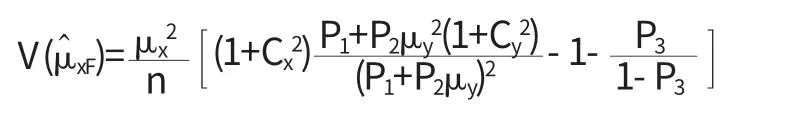
在所有的随机化回答技术中，个体参与调查的合作程度均依赖于调查装置对个体作出回答的保密程度，装置对个体隐私的保密性越好，个体越容易配合调查.另一方面，如果装置对个体的保护程度提高了，那么装置的调查效率就会降低.因此装置对个体的保护度与装置的调查效率之间存在着不可调和的矛盾.为了在保护度与效率之间建立一种合理的平衡，已有很多学者在这方面作出了研究.

〔1〕Hong Zhimin.Estimation of mean in randomized response surveys when answers are incompletely truthful[J].Model Assisted Statistics and Applications,2006,(1).

〔2〕闫在在，聂赞坎.随机化策略的公平比较[J].数学物理学报，2004(24).

〔3〕洪志敏，闫在在.基于相同保护度的随机化装置效率比较[J].工程数学学报,2008(25).

〔4〕冯士雍，施锡铨.抽样调查—理论，方法和实践[M].上海：上海科学技术出版社,1994.

〔5〕谢邦昌.抽样调查理论及其应用方法[M].北京：中国统计出版社,1998.