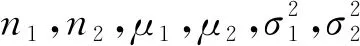一个可供选择的全随机化模型

董俊超

(烟台大学数学与信息科学学院,山东 烟台 264005)

1965年WARNER[1]第一次引进了随机化抽样方法,用于处理定性敏感性问题的抽样调查，随后这种方法得到了很大的发展。大体思路为:首先是对定性敏感性问题随机化方法进行各种各样的优化，这方面的研究成果很多，本文不再赘述; 随后GREENBERG等[2]把随机化方法扩展到定量敏感性问题。 目前,对于定量敏感性问题的随机化技术，按照文献[3-4]的观点，可把它分为3类：全随机化模型(full randomized response model)，偏随机化模型(partial randomized response model)，可选性随机化模型(optional randomized response model)．

全随机化模型最早在文献[5]中有提及,详细的论述在文献[6], 它的优点是对被调查者的真实数据进行编码,可以更好地保护被调查者的隐私, 适合高敏感性问题的抽样调查, 比如吸毒、贩卖军火等等。偏随机化模型最早在文献[7]中对定性敏感性问题有提及, 在文献[8]中有详述, 该方法是由被调查者做一个随机试验，由试验的结果决定被调查者做真实的回答还是对真实信息进行编码再回答。可选性随机化模型在文献[3-4,9]中有论述, 该方法是由被调查者自身决定，感觉被调查的问题敏感就进行编码回答，否则就进行真实回答。GREENBERG等[2]的随机化模型是被调查者根据随机试验的结果给出敏感性问题的真实答案或一个无关问题的答案,其可以归结到偏随机化模型中。

1 提出新模型

Zad=Y+X。

(1)

另一个为乘随机化模型(multiplication randomized response model), 其编码的方法是, 由被调查者利用随机试验抽取一个服从X分布的随机数乘上自身的敏感性指标报告给调查者。 若用Zmu表示观察到的变量,该模型可表达为:

Zmu=YX。

(2)

无论是加随机化模型还是乘随机化模型,编码方法均比较单一, 可能会造成被调查者的不信任感,害怕自身的隐私被泄露。比如在偷税的调查中, 如果一个被调查者自身的指标比较大,而抽到的随机数又较大, 这时无论对加随机化模型还是乘随机化模型, 都会造成被调查者心理上的某种不安或恐惧，从而可能造成不真实的回答， 得到不可靠的数据。 本文提出一个新模型,给被调查者一个选择, 由他们根据自身的愿望选择编码方法。 具体做法为: 从总体中按放回方式抽取一个样本, 每个被调查者再做一个随机试验, 按照放回方式抽取分布为X的一个随机数, 由被调查者根据自身的意愿选择是把自身的敏感指标加上或者减去该随机数, 然后报告给调查者。 假定总体中有以概率p的被调查者选择“加”, 以概率1-p的被调查者选择“减”，该模型可表示为

(3)

其中，p是一个未知参数,由总体的性质所确定，它的期望为

E(Z)=pE(Y+X)+(1-p)E(Y-X)=

μy+(2p-1)μ。

(4)

它的方差为

V(Z)=E(Z2)-E2(Z)=pE(Y+X)2+

(1-p)E(Y-X)2-E2(Z)=

E(Y2)+E(X2)+2(2p-1)E(YX)-E2(Z)=

(σy2+μy2)+σ2+μ2+

2(2p-1)μyμ-(μy+(2p-1)μ)2=

(5)

(6)

(7)

进一步,有

(8)

其中，V(Zi)是把式(5)中的μ换为μi,σ换为σi(i=1,2)所得。

定理1得证。

由于样本方差是总体方差的无偏估计,所以很容易得到下面定理:

(9)

2 新模型与已有模型的比较

下面就本文提出的模型(3)，在隐私保护度及估计量的精度方面与已有的模型作比较。

2.1 保护度的比较

YAN等[10]提出了对模型保护度的一个计算方法。 现计算该模型的保护度：

Δ=E(Z-Y)2=

pE(X2)+(1-p)E((-X)2)=

E(X2)=σ2+μ2。

(10)

对于加随机化模型(1), 根据文献[5]中结论, 该模型对被调查者的保护度为

Δad=σ2+μ2。

(11)

对于乘随机化模型(2), 根据文献[10]中计算结果, 该模型对被调查者的保护度为

(12)

2.2 精度的比较

(13)

(14)

3 结束语