滑坡残余强度预测

(中国地质大学(武汉) 工程学院，湖北 武汉，430074)

滑坡残余强度对滑坡特别是老滑坡的稳定性评价非常重要，其研究方法主要通过试验手段，包括反复直剪试验、环剪试验、三轴剪切试验和原位剪切试验等。目前国内外许多学者对其进行了研究。文献[1]介绍了滑坡滑带土残余强度的影响因素、测试仪器、试验方法等方面的研究现状。王恭先[2]结合中铁西北科学研究院环剪试验的成果，介绍了滑坡残余强度与滑带土黏粒含量、砾石含量、初始密度、初始含水率、剪切速率等影响因素之间的关系。Wan等[3]采用直剪试验和环剪试验对含55%～74%(质量分数)非晶质黏土矿物的滑坡原状样进行了研究，研究表明非晶质黏土矿物增加了土颗粒之间的黏聚力，导致峰值强度增高，而非晶质黏土矿物为粉土和砂土颗粒的相互作用提供了接触面，其导致滑坡残余内摩擦角较小。张芳枝等[4]采用排水反复直剪试验对东深供水工程风化泥质软岩在长期浸水软化后的残余强度变化规律进行了探讨。左巍然等[5]采用直剪仪反复剪切试验对原状土、击实土和静压土这3种状态膨胀土的残余强度进行了研究，研究表明，膨胀土的残余强度与它的结构和应力历史没有直接联系。张昆等[6]采用现场大剪试验研究了残余强度与峰值强度的关系，并得到了残余强度的估算方法。郭惠丰等[7]采用三轴试验研究了粗晶大理岩在应力平行层理状态和应力垂直层理状态，2种情况下岩石残余强度与围压的关系。郭富利等[8]通过三轴力学试验，研究了围压和饱水时间对软岩残余强度和峰后体积变化的影响规律、围压和饱水时间对软岩残余强度和体积变化的作用机制及特点。米海珍等[9]采用静三轴试验，探讨了兰州黄土与石灰配制而成的灰土残余强度在浸水条件下的变化规律，研究表明，灰土的残余强度与其围压呈线性关系。王瑞红等[10]通过循环加卸载试验，对处于残余强度状态岩样在不同围压、不同卸荷量条件下残余强度的变化规律，试验结果表明：岩样在不同围压和不同卸荷量条件下残余强度与循环次数呈指数变化规律。谭文辉等[11]采用原位剪切试验对某巨型黄土滑坡剪出口3个不同位置的土样进行了天然状态和饱水状态2种工况下的残余剪切强度进行了研究，获得相应的残余抗剪强度指标，并总结了黄土滑坡原位剪切试验过程中的注意事项。但是，滑坡残余强度试验研究有很多不确定因素，导致试验结果不理想，并且试验花费时间长，价格昂贵。为此，本文作者以滑坡基本物理参数为基础，从区域统计规律出发，采用 SPSS数学分析软件对滑坡残余强度的相关影响因素进行筛选，然后以区域典型滑坡为例，分别采用神经网络模型和多元回归模型对该滑坡的残余强度进行预测，最后对其预测结果进行对比分析。

1 相关影响因素筛选

为了研究滑坡残余强度的区域统计规律，本文选取了万州区20个具有相同基本特征、相似工程地质条件的滑坡不同部位共147个滑带土样基本物理力学参数进行分析，其选取的滑坡具有以下基本特征：均为堆积层滑坡，滑面为岩土接触面，滑体物质一般由粉质黏土、砂泥岩块石、人工填土组成，滑带由粉质黏土夹砂泥岩角砾，滑床为侏罗系砂泥岩。

为了筛选滑坡抗剪强度的相关影响因素，采用大型数学分析软件 SPSS分析天然含水率、密度、饱和度、孔隙率、孔隙比、液限、塑性、液性指数、塑性指数、压缩模量、压缩系数、天然峰值强度、饱和峰值强度与残余强度的相关性。由于数据量太大，且滑坡大多与降雨有关，因此，这里主要研究滑坡基本物理力学参数与滑坡饱和残余强度的相关性，具体见表1。

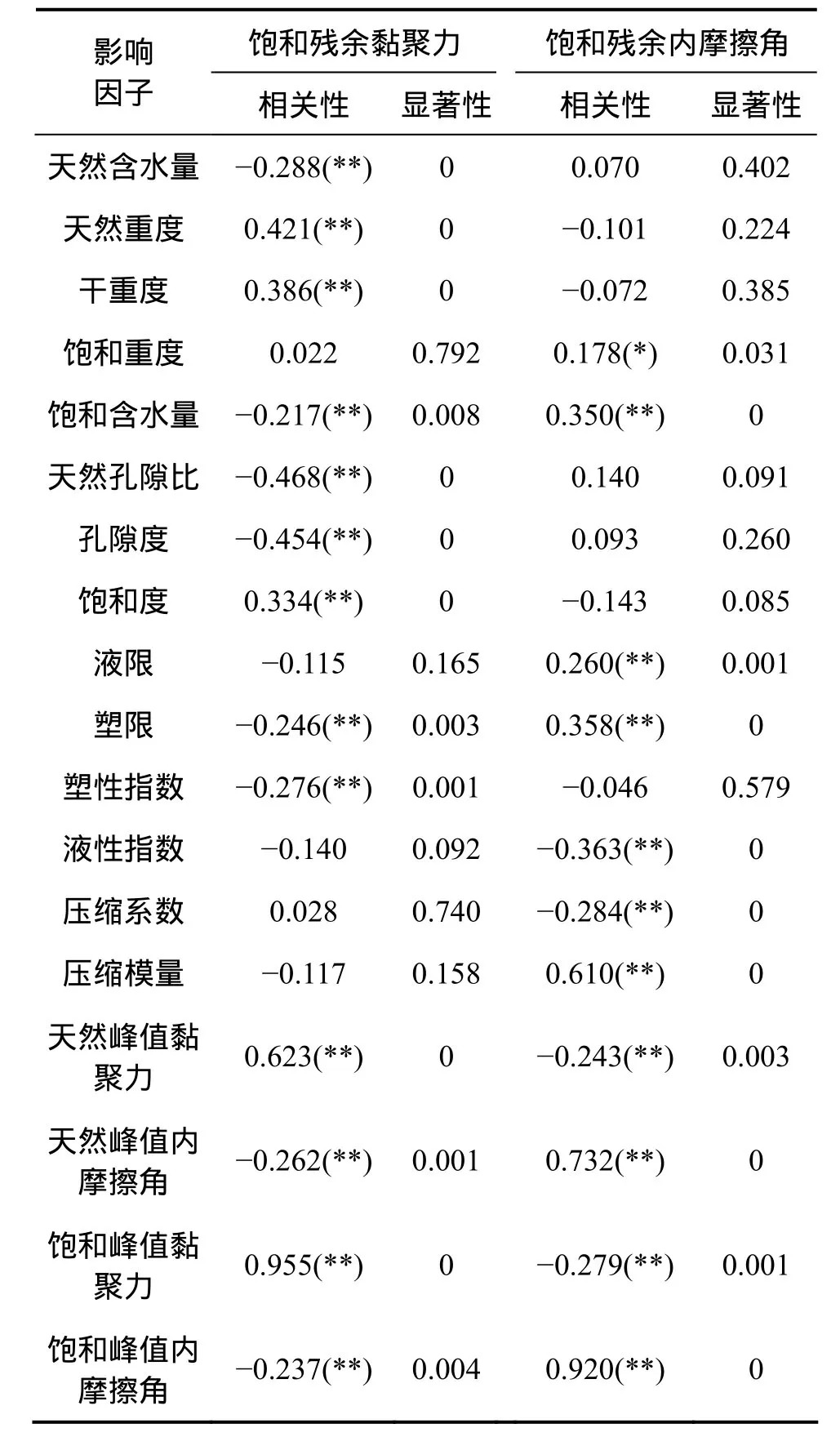
表1 滑坡饱和残余强度影响因子分析Table 1 Influence factors of landslide saturated residual strength

由表1可知：饱和残余黏聚力与天然含水量、天然重度、干重度、天然孔隙比、孔隙度、饱和度、天然峰值黏聚力、饱和峰值黏聚力的显著性为 0，说明这些参数与饱和残余黏聚力完全相关，这些因素为饱和残余黏聚力的相关影响因素；而饱和残余内摩擦角与饱和含水量、塑限、液性指数、压缩系数、压缩模量、天然峰值内摩擦角、饱和峰值内摩擦角的显著性为 0，说明这些参数与饱和残余内摩擦角完全相关，这些因素为饱和残余内摩擦角的相关影响因素。

2 万泉滑坡概况

2.1 滑坡概述

万泉滑坡位于长江一级支流龙宝河左岸，一级阶地及其以上地带，属侵蚀堆积地貌及构造—剥蚀中切割低山丘陵河谷地貌。以鹰咀岩为界，将万泉滑坡分为东滑坡区及西滑坡区，两滑坡区相距250 m，其中西区前缘最低高程为191 m，后缘最高高程为265 m，总面积为15.15×104m2，体积为155.28×104m3，东区前缘最低高程为192 m，后缘最高高程为267 m，总面积19.43×104m2，总体积为244.4×104m3。

2.2 滑坡物质组成

2.2.1 滑体

(1) 杂填土。主要分布于西滑坡区厂区及居民住宅区，为紫红、紫褐色黏土夹碎块石，夹砂、泥岩碎块石，砖瓦块、煤炭渣、混凝土及生活垃圾等。覆盖于地表最上层，厚2～3 m。

(2) 碎裂状岩体。主要分布于西滑坡区文体广局7～9剖面一带，黄家湾及宝山路内侧，在道路开挖中边坡上也有出露，地表出露东西宽180 m，南北长90 m，最大厚度26 m。由碎裂状紫红色粉砂质泥岩夹泥质粉砂岩及粉砂岩透镜体组成。

(3) 粉质黏土夹碎块石。分布广泛，厚度变化大，总体上滑体前后缘薄、中部较厚，主要由紫红色粉质黏土及泥(砂)岩块石组成，可塑—硬塑状。见水后具强黏性，有滑感，含 25%～60%的碎块石，粒径为 3～2 500 mm。

2.2.2 滑带

根据地面调查、勘探工程揭露，滑体底部滑动带(面)受基岩(主要为泥岩)顶界面控制，沿堆积层与基岩接触的薄弱带滑动剪出。滑面深度2.40～34.70 m；东、西滑坡区滑带土物质组成及特征基本相似；滑带土为褐黄色，灰紫色、暗紫红色及灰白色黏性土，湿润，可塑，局部呈软塑。

2.2.3 滑床

万泉滑坡的滑床为侏罗系中统上沙溪庙组(J2s)，主要为紫红色泥岩及粉砂质泥岩夹粉砂岩，滑床岩层倾向为 320°～330°，倾角为 3°～7°，倾向坡内，有利于岩体稳定。

2.3 万泉滑坡基本物理力学参数

根据中国建筑西南勘察设计研究院完成的《重庆市三峡库区三期地质灾害防治工程非应急项目万州区万泉滑坡详细勘查报告》室内试验结果，该滑坡滑带土物理力学参数及残余强度试验值如表2所示。

表2 万泉滑坡物理力学参数Table 2 Wanquan landslide physical and mechanical parameters

3 滑坡残余强度预测

3.1 多元回归模型预测

设预测对象为y，影响因素有m个，分别为x1,x2, …,xm，

对于预测对象y为饱和残余黏聚力时，其影响因素有8个，分别为天然含水量、天然重度、干重度、天然孔隙比、孔隙度、饱和度、天然峰值黏聚力和饱和峰值黏聚力，其编号依次为x1,x2, …,x8。

采用模型原理，利用上述147组滑带土数据，可得滑坡饱和残余黏聚力的预测模型为

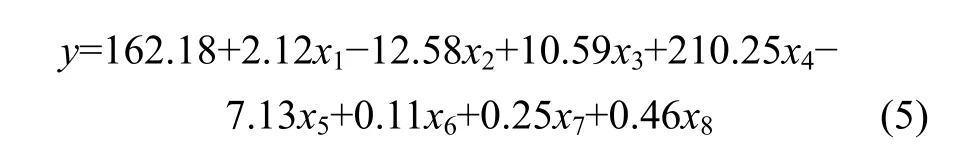
将表2中相应数据代入式(5)，可得饱和残余内摩擦角的预测结果。

对于预测对象y为饱和残余内摩擦角时，其影响因素有7个，分别为饱和含水量、塑限、液性指数、压缩系数、压缩模量、天然峰值内摩擦角、饱和峰值内摩擦角，其编号依次为x1,x2, …,x7。

采用模型原理，利用上述147组滑带土数据，可得滑坡饱和残余内摩擦角的预测模型为：

将表2中相应数据代入式(6)，可得饱和残余内摩擦角的预测结果。多元回归模型预测结果如表3所示。

表3 多元回归模型预测结果Table 3 Prediction results of multiple regression model

3.2 神经网络模型预测

BP神经网络模型[13]是一种按误差逆传播算法训练的多层前馈网络。BP神经网络能学习和存贮大量的输入−输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)。其具体建立过程如下。

第1步：确定网络结构：根据样本数据确定输入层、隐层以及输出层的神经元节点数。

第2步：网络初始化：初始化输入层与隐层、隐层与输出层之间的网络连接权重，初始化隐层与输出层的网络阀值，制定学习速率和激励函数。

第3部：计算隐层输出：根据输入向量、输出层和隐层的连接权值以及隐层阀值计算隐含层输出值。

第4步：计算输出层输出。

第5步：计算误差。

第6步：重新计算权值。

第7步：重新计算阀值。

第8步：判断是不是满足误差要求，如果不满足就返回第3步计算直到满足误差要求终止计算。

对于饱和残余黏聚力和饱和残余内摩擦角，均选取 DPS数据处理系统的 BP神经网络子系统，采用matlab软件进行编程，通过不断调试，最终选取的BP神经网络模型如下：输入层为 5个输入节点, 输出层为1个输出节点，隐层15个节点,传递函数(包括隐层函数和输出函数)和训练函数为：logsig，purelin和trainlm。

训练采用的数据为上述147组滑带土的物理力学参数，具体训练参数见表4。

表4 神经网络模型训练参数Table 4 Training parameters of neural network model

将表2中相应数据代入相应的训练网络，其预测结果如表5所示。

表5 神经网络模型预测结果Table 5 Prediction results of neural network model

3.3 预测结果对比分析

根据表2、表3和表5，对滑坡饱和残余强度预测结果与试验值进行对比，结果如表6所示。

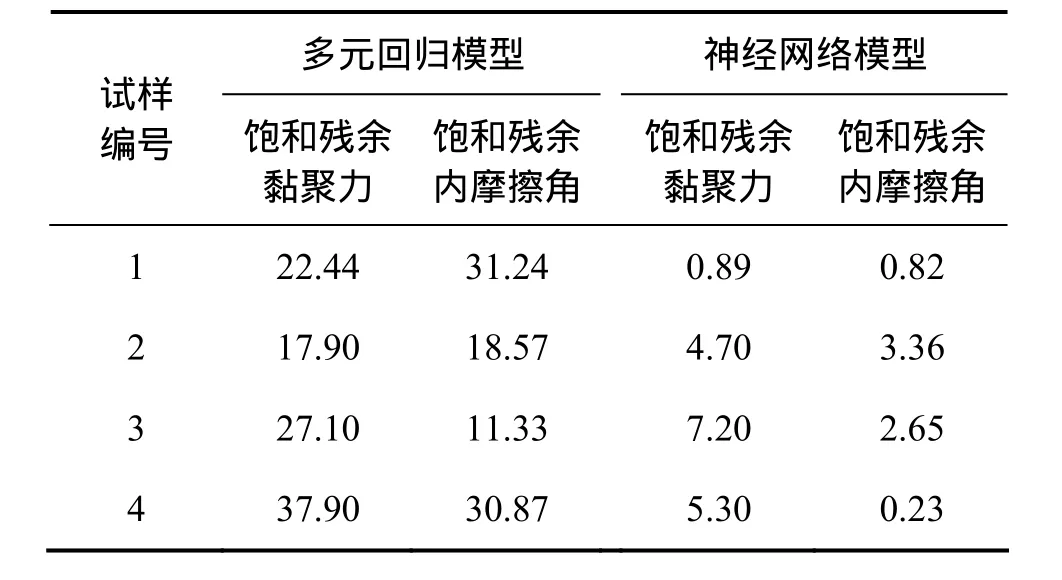
表6 滑坡残余强度预测结果与试验值的相对误差Table 6 Relative error between landslide residual strength prediction results and test values %

由表6可知：对于饱和残余黏聚力，多元回归模型与试验值的相对误差为17.90%～37.90%，而神经网络预测模型的相对误差为0.89%～7.20%；对于饱和残余内摩擦角，多元回归模型与试验值相对误差为11.33%～31.24%，而神经网络预测模型的相对误差为0.23%～3.36%。可见：神经网络预测模型的预测精度更高。究其原因，可能是由于这里采用的多元回归模型为线性模型，没有考虑影响因素与残余强度的非线性关系。

4 结论

(1) 万州区典型堆积层滑坡饱和残余黏聚力的相关影响因素为天然含水量、天然重度、干重度、天然孔隙比、孔隙度、饱和度、天然峰值黏聚力和饱和峰值黏聚力；饱和残余内摩擦角的相关影响因素为饱和含水量、塑限、液性指数、压缩系数、压缩模量、天然峰值内摩擦角、饱和峰值内摩擦角。

(2) 万州区典型堆积层滑坡饱和残余黏聚力和饱和残余内摩擦角相应的多元回归预测模型为：y=162.18+2.12x1−12.58x2+10.59x3+210.25x4−7.13x5+0.11x6+0.25x7+0.46x8和y=7.63−0.03x1−0.3x2−3.99x3+7.31x4+0.13x5−0.46x6+0.99x7。

(3) 万州区典型堆积层滑坡饱和残余强度的神经网络模型为：输入层为5个输入节点, 输出层为1个输出节点，隐层 15个节点,传递函数和训练函数为：logsig，purelin和trainlm。

(4) 多元回归模型与试验值的相对误差为10%～40%，而神经网络预测模型的相对误差基本都在5%左右，神经网络预测模型的预测精度更高。神经网络模型比多元回归模型更适合于预测万州区典型堆积层滑坡的残余强度。

[1] 滑坡文集编委会.国内外滑带土残余强度的研究现状[C]//滑坡文集(Ⅱ).北京: 人民铁道出版社, 1979: 210−219.Editorial Committee of Landslide Corpus.Research status of residual strength on slip soil at home and abroad[C]//Landslide Corpus (Ⅱ).Beijing: People’s Railway Publishing House, 1979:210−219.

[2] 王恭先.滑坡防治中的关键技术及其处理方法[J].岩石力学与工程学报, 2005, 24(21): 3818−3827.WANG Gongxian.Key technique in landslide control and its handling measures[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(21): 3818−3827.

[3] Wan Y, Kwong J.Shear strength of soils containing amorphous clay-size materials in a slow-moving landslide[J].Engineering Geology, 2002, 65(4): 293−303.

[4] 张芳枝, 陈晓平, 吴煌峰, 等.东深供水工程风化泥质软岩残余强度特性研究[J].工程地质学报, 2003, 11(1): 54−57.ZHANG Fangzhi, CHEN Xiaoping, WU Huangfeng, et al.The characteristic of residual strength of soft clayey rocks of the east river-shenzhen water supply project[J].Journal of Engineering Geology, 2003, 11(1): 54−57.

[5] 左巍然, 杨和平, 刘平.确定膨胀土残余强度的试验研究[J].长沙交通学院学报, 2007, 23(1): 23−27.ZUO Weiran, YANG Heping, LIU Ping.Study on the determination of residual strength for expansive soil[J].Journal of Changsha Communications University, 2007, 23(1): 23−27.

[6] 张昆, 郭菊彬.滑带土残余强度参数试验研究[J].铁道工程学报, 2007, 24(8): 13−15, 26.ZHANG Kun, GUO Jubin.Experimental research on the residual strength parameters of slip soils[J].Journal of Railway Engineering Society, 2007, 24(8): 13−15, 26.

[7] 郭惠丰, 伞桂兰.三轴残余强度以及全过程曲线出现蠕变的成因[J].工程兵工程学院学报, 1999, 14(1): 68−70.GUO Huifeng, SAN Guilan.The cause of 3-axis residual strength and emerging creep in whole process curve[J].Journal of Nanjing Engineering Institute, 1999, 14(1): 68−70.

[8] 郭富利, 张顶立, 苏洁, 等.围压和地下水对软岩残余强度及峰后体积变化影响的试验研究[J].岩石力学与工程学报,2009, 28(Z1): 2644−2650.GUO Fuli, ZHANG Dingli, SU Jie, et al.Experimental study of influences of confining pressures and ground water on residual strength and post-peak volumetric change of soft rock[J].Chinese Journal of Rock Mechanics and Engineering, 2009,28(Z1): 2644−2650.

[9] 米海珍, 王昊, 高春, 等.灰土的浸水强度及残余强度的试验研究[J].岩土力学, 2010, 31(9): 2781−2785.MI Haizhen, WANG Hao, GAO Chun, et al.Study of immersion strength and residual strength of lime-loess[J].Rock and Soil Mechanics.2010, 31(9): 2781−2785.

[10] 王瑞红, 李建林, 蒋昱州, 等.循环加卸载对岩体残余强度影响的试验研究[J].岩石力学与工程学报, 2010, 29(10):2103−2109.WANG Ruihong, LI Jianlin, JIANG Yuzhou, et al.Experimental research on influence of cyclic loading and unloading on rock mass residual strength[J].Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 2103−2109.

[11] 谭文辉, 任奋华, 苗胜军.峰值强度与残余强度对边坡加固的影响研究[J].岩土力学, 2007(S1): 616−618.TAN Wenhui, REN Fenhua, MIAO Shengjun.Influence of parameters of peak strength and residual strength on the reinforcement of slopes[J].Rock and Soil Mechanics, 2007(S1):616−618.

[12] 殷坤龙.滑坡灾害预测预报[M].武汉: 中国地质大学出版社,2003: 35−36.YIN Kunlong.Landslide hazard prediction[M].Wuhan: China University of Geosciences Press, 2003: 35−36.

[13] 郭晶, 孙伟娟.神经网络理论与 MATLAB 7实现[M].北京:电子工业出版社, 2005: 110−112.GUO Jing, SUN Weijuan.Neural network theory and implementation by MATLAB 7[M].Beijing: Electronic Industry Press, 2005: 110−112.