高压大流量水阀U形密封圈失效机理
陈国强 ,谭建平,陈晖
(1.中南大学 机电工程学院,湖南 长沙,410083;2.湖南工程学院 机械工程学院,湖南 湘潭,411101)
大型水压机水路系统具有高压大流量特点,由于U形橡胶密封圈结构简单,安装维护方便,被广泛应用在高压低速往复滑动密封场合。通过对300 MN模锻水压机的故障统计发现,1 a内水路系统主分配器上8个水阀的阀杆U形往复密封圈共发生了214次失效,主要失效形式表现为短时间内由于强度失效导致的密封击穿,这严重影响了设备的正常运行。由于水的润滑性差且水阀结构不便于进行润滑,使得往复滑动密封成为高压水阀设计和维护的难点。开展U形密封圈的失效机理研究,可为密封设计和维护提供理论依据。国内外学者已对O形密封圈进行了比较深入和系统的研究[1−2],但由于唇形橡胶密封件具有材料、几何及载荷的三重非线性特征[3],给研究工作带来极大难度。近年来,数值仿真技术的发展促进了对唇形密封性能的研究,Kim 等[4]基于有限元法开展了非规则唇形密封圈静接触应力分析;Maoui等[5]仿真分析一种密封圈弹性唇口的变形对密封效果的影响;文献[6−8]等基于有限元法分析了Y形和X形等唇形橡胶密封圈的接触应力变化规律及应力集中位置。但现有研究仍存在以下不足:(1) 液压系统均以中、低压油为介质,没有针对以高压水为介质开展研究;(2) 研究对实体模型进行较大简化,大部分研究进行的是二维分析;(3)缺少对动态下的唇形密封失效机理的研究。为此,本文作者以高压大流量水阀阀杆的U形橡胶往复滑动密封结构为对象,基于三维非线性接触动力学仿真,系统研究高压背景下U形密封圈的失效机理,得到密封失效条件和各因素的影响规律。
1 U形密封结构及受力分析
大型水压机高压大流量水阀采用JB 2025—76标准,水阀及阀杆密封的结构如图1所示[9]。阀杆的上、下往复密封均采用U形橡胶密封圈,利用其唇口受压后贴紧阀杆表面而实现密封。
U形密封圈在工作时主要受到液压介质压应力、接触应力、滑动摩擦力、阀杆横向振动挤压力及阀体支撑力等多种力的共同作用,其中前4种受力是影响密封性能及密封圈应力的主要因素。理想工况下密封圈受力情况如图2所示。图2中:PL为液压介质压力;Fc为接触压力;Ff为滑动摩擦力;FN1和FN2为阀体的约束力。
1.1 对液压介质压力PL的分析
液压介质直接作用在密封圈上表面而产生压应力。水路系统作为水压机工作的主要载体,在工作状态转换时内部会出现复杂的动态特性,导致液压冲击。因而,液压介质压力包括系统正常工作压力及因液压冲击产生的压力。刘江明[10]的研究表明:300 MN模锻水压机在32 MPa的工作压力下转换工况时会产生10 MPa的液压冲击。
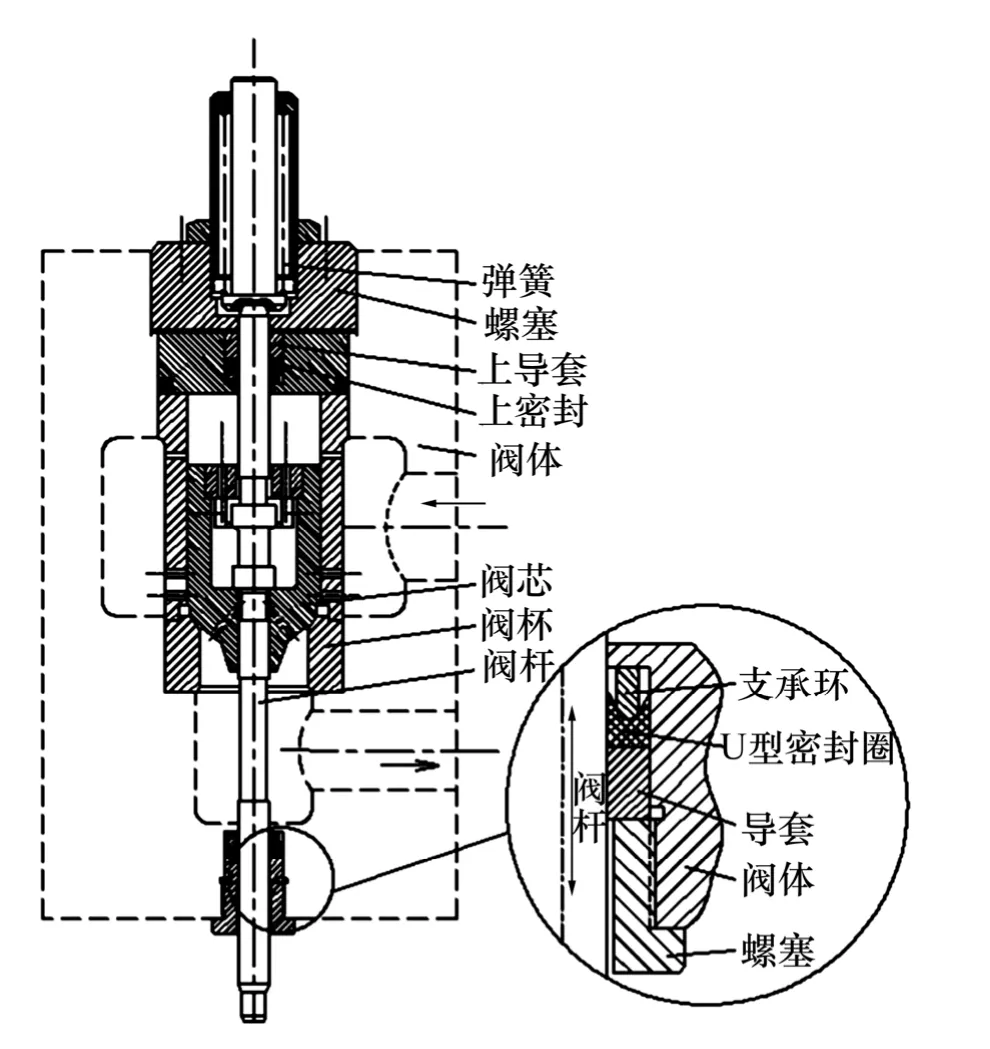
图1 水阀密封结构Fig.1 U-ring seal structure diagram of water valve

图2 密封圈受力示意图Fig.2 Force schematic diagram of U-ring seal
1.2 对接触压力Fc的分析
接触压力是密封失效判据的首要条件,其大小受工作介质内压力、预紧压应力、阀杆径向摆动挤压力等因素影响。稳定状态下U形密封圈的接触压力可表示为:
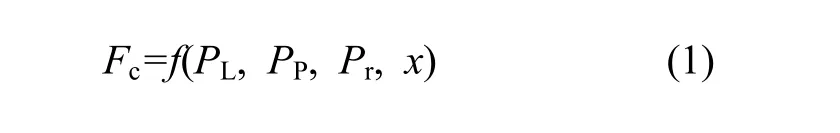
其中:PL为液压介质压力;PP为预紧压应力;Pr为阀杆径向挤压力;x为密封圈轴向距离。
液压介质压力PL是产生接触应力的主要原因。对于动密封装置,由于运动学及工艺装配等原因,配合件之间通常存在着一定的间隙,从而使得预紧压应力PP消失。当系统不稳定时,阀杆产生一定的径向振动和弹性变形,导致密封圈受到径向挤压力,接触应力随x的变化为非线性关系,此时,无法用式(1)来准确表达接触压力的大小。
1.3 对摩擦力Ff的分析
阀杆运动时为滑移接触,会产生滑动接触摩擦力,摩擦力方向与阀杆运动方向相反,是密封圈轴向切应力的根源。由于橡胶是低弹性模量的黏弹体,在很宽频域范围内均具有很高的内摩擦,这使得真实接触面积与接触压力之间呈非线性关系,运动摩擦力Ff可按照下式进行计算[11]:
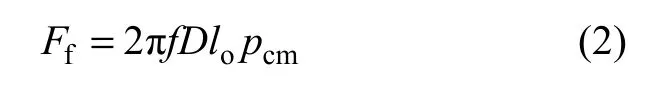
其中:f为摩擦因数;lo为接触面的宽度;D为密封圈的摩擦面直径;pcm为接触面的平均压力。
接触压力与摩擦因数是影响接触摩擦力大小的主要因素。由于不能精确地给出接触面上的接触压力,因而,无法利用式(2)进行准确计算。
2 基于LS-DYNA的U形密封动力学仿真
由于阀杆密封接触为复杂的非线性接触,选用ANSYS/LS-DYNA软件进行 U形往复密封的三维非线性接触动力学仿真,进而得到各因素对U形往复密封性能和应力状况的影响规律,确定密封失效的边界条件。
2.1 有限元模型的建立
基于LS-DYNA进行非线性接触分析时,不允许有初始接触[12]。考虑工艺间隙和磨损,设定阀杆和密封圈的双边间隙为0.05 mm,以阀杆下端密封圈为对象进行分析,在 CAD中建立三维模型并导入LS-DYNA软件。选用三维实体非线性显式单元SOLID164,先将U形密封圈实体模型用平面切割成2部分,再通过扫略操作将其全部划分成规则的六面体单元。设定阀杆单元边长为1.2 mm,密封圈单元边长为0.7 mm,共得到41 200个节点和35 268个单元,有限元网格模型如图3所示。
2.2 材料模型及参数的确定
橡胶材料模型是能否完成仿真分析的关键。作为一种非线性弹性材料,橡胶的应力应变函数是一个复杂的非线性函数,国内外学者提出多种模型来描述橡胶材料,如Mooney-Rivlin,Blatz-Ko以及Yeoh模型等[1,13−14]。其中用Mooney-Rivlin模型能很好地描述变形小于 150%的橡胶材料力学性能,在橡胶材料力学性能分析中被证明应用效果良好[7−8]。因此,选用两参数的 Mooney-Rivlin表征橡胶的模型,其应变能密度函数(W)为[14]:
(2)交易成本低廉。比特币的交易不需要中介机构,交易成本低廉(但对小额交易而言,成本较高)。同时,比特币中的用户采用的是假名,国家很难收取比特币的交易税。

图3 U形密封结构有限元模型Fig.3 Finite element model of U-ring seals structure

其中:I1和I2为变形张量不变量;C10和C01为力学性能常数。
在小应变时,橡胶材料弹性模量E与剪切模量G有下述关系:

对于橡胶材料的泊松比μ为0.49,有E≈3G。
两参数的 Mooney-Rivlin模型材料常数可利用硬度计测得橡胶试样的硬度Ha,得:

再利用经验公式C10+C01=E/6,C01=0.25C10,计算得到C10=1.04,C01=0.26。
阀杆为线性钢材,密度为 7.8 t/m3,弹性模量E=210 GPa,泊松比μ=0.3,剪切模量为79.4 GPa。
2.3 仿真条件及参数设置
在实际应用中,阀杆的最大运动速度为0.06 m/s,液压介质工作压力为32 MPa,约定阀杆往上运动为正向,往下运动为反向。由于阀杆与密封圈接触状况不清楚,故选用自动单面接触,LS-DYNA程序将自动判定接触表面及方向。根据实际情况对橡胶密封圈的外侧面施加全约束,底面施加垂直方向的位移约束,定义阀杆和密封圈各方向的初始速度均为0 m/s,液压介质的压力载荷垂直施加在密封圈上表面单元节点上。前期分析发现控制最小时间步长为−1×10−7时存在负体积现象,故需进行质量缩放,将时间步长因子设为0.6。
2.4 仿真及结果分析
在稳定状态时阀杆静止,不需要考虑接触摩擦,当阀杆上下运动时密封圈受力状况受到密封接触应力、阀杆运动速度、液压介质压力、接触摩擦因数、阀杆径向受力等因素影响。下面应用Von-Mises应力作为衡准,对各因素的影响进行仿真分析。
(1) 阀杆静止时介质压力是影响密封性能的主要因素,仿真得到密封结构的应力云图和最大应力随介质压力变化的规律如图4和图5分别所示。

图4 阀杆静止时密封结构应力云图(p=32 MPa)Fig.4 Stress nephogram of seal structure under static state(p=32 MPa)
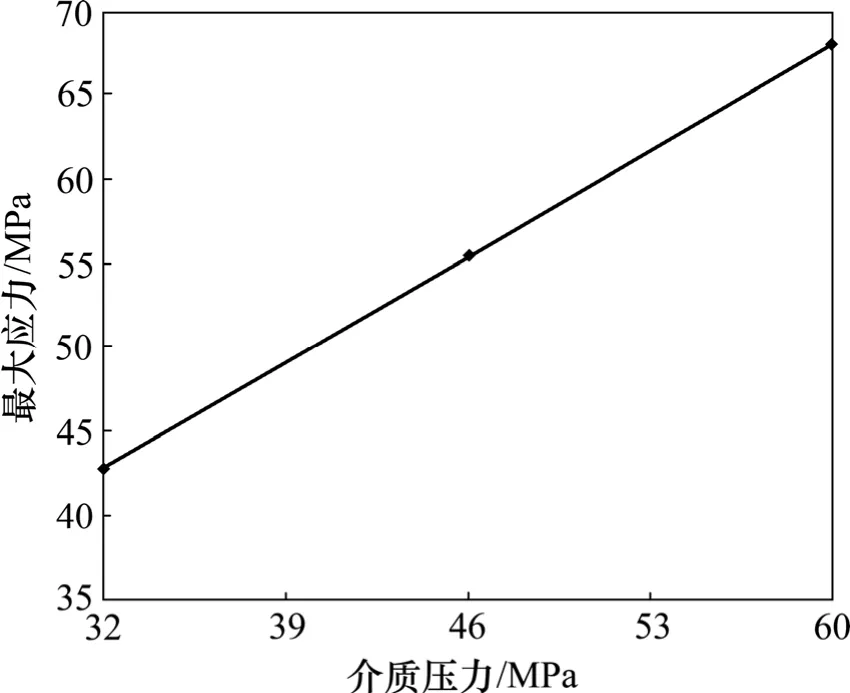
图5 阀杆静止时最大应力变化曲线Fig.5 Maximum stress curve of U-ring seals with medium pressure changes
从图4和图5可见:静止时U形密封圈的最大应力发生在密封圈的底槽,且比工作介质压力高 8~10 MPa,由于丁腈橡胶的撕裂强度为76~94 MPa[15],可以判定当液压介质压力在66 MPa以内时密封圈处于安全状态。
(2) 由于 U形密封圈具有滑动摩擦因数小的特点,在此取f为0.2,得阀杆向上运动时密封圈的应力分布如图6所示,最大接触应力与密封圈最大应力随速度变化的分布曲线如图7所示。
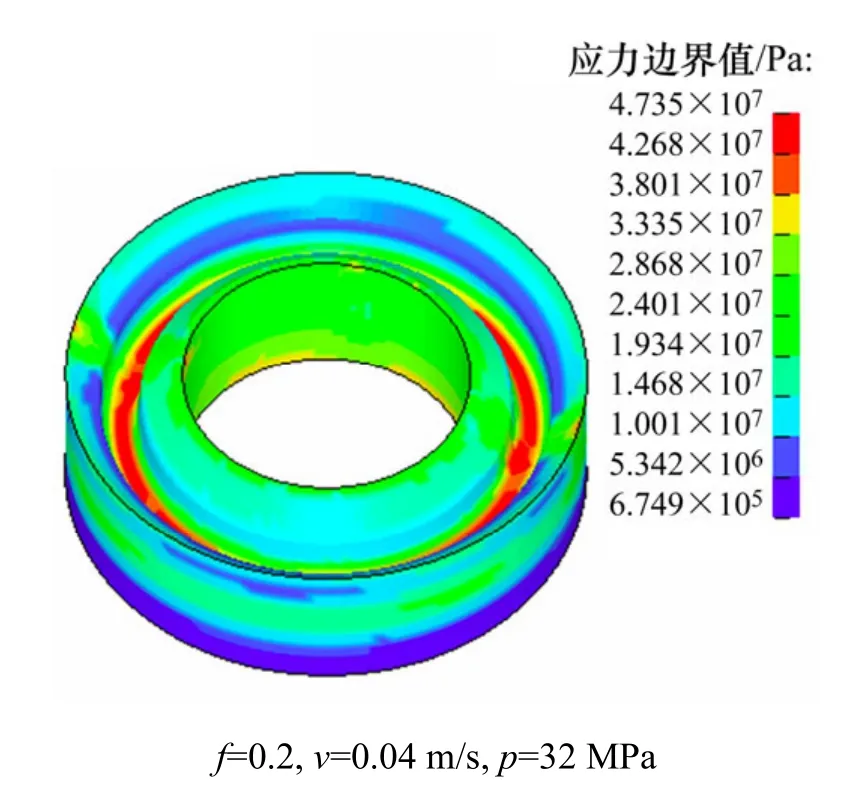
图6 阀杆正向运动时密封圈应力云图Fig.6 U-ring seal’s stress nephogram of valve stem move forward
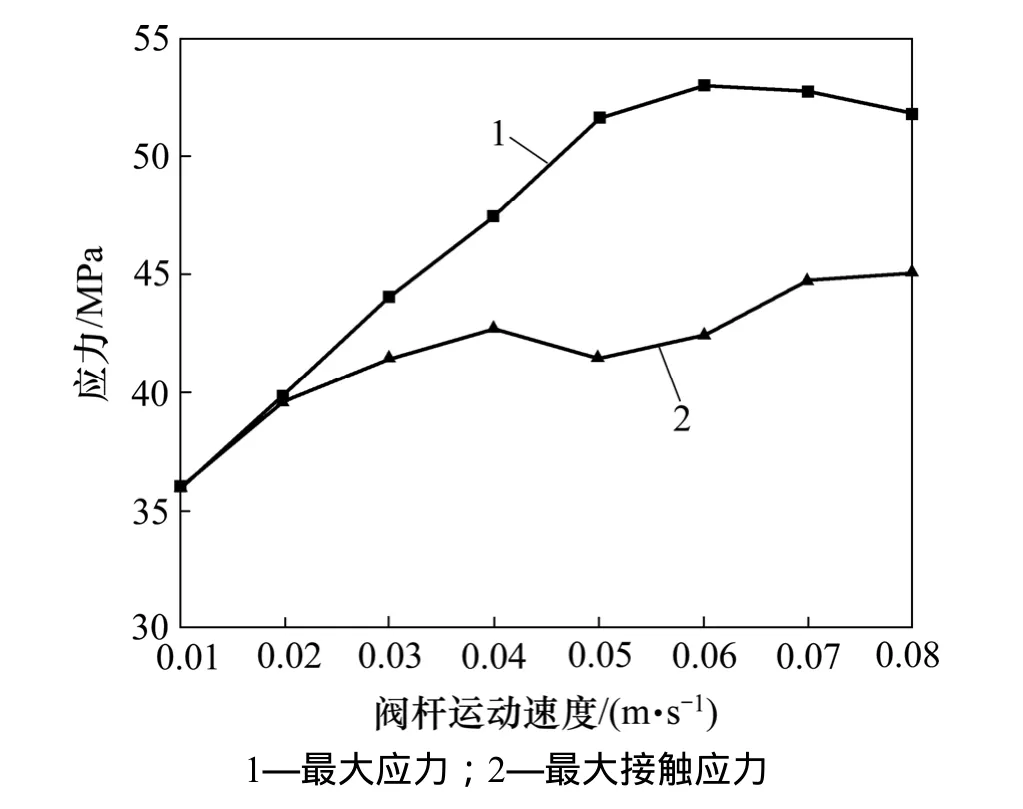
图7 最大接触应力和最大应力随速度变化曲线(f=0.2, p=32 MPa)Fig.7 Curve of maximum contact stress and maximum stress with speed changes
从图6和图7可见:当阀杆正向运动时,密封圈最大应力集中在密封圈沟槽部位,且最大应力随阀杆运动速度增大而递增,当速度达到0.05 m/s时最大应力变化趋于稳定,最大接触应力的变化相对平稳,且比最大应力小。此时,最大应力值低于橡胶材料的撕裂强度,故处于安全状态。
(3) 在介质压力为32 MPa时,取不同的摩擦因数f和阀杆速度进行分析,得到密封圈最大应力随摩擦因数及阀杆速度变化的影响规律如图8所示。
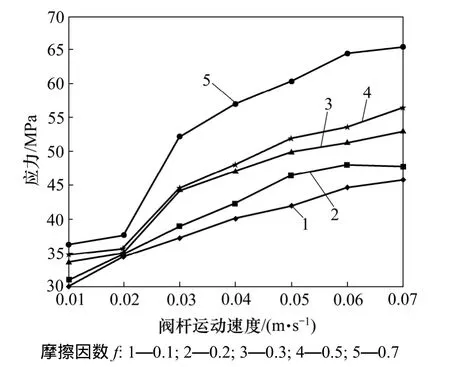
图8 阀杆正向运动时最大应力随速度变化曲线(p=32 MPa)Fig.8 Maximum stress curve of U-ring seal with speed changes
从图8可见:阀杆正向运动时摩擦因数变化对密封圈最大应力的影响显著,当摩擦因数f在0.2以内时,密封圈最大应力随阀杆滑动速度的增加成近似成正比增大,当速度达到0.06 m/s时趋于稳定。图8还说明阀杆正向运动时,在最大运行速度内密封圈最大应力均低于橡胶材料的撕裂强度,表明在此状态下密封圈可以安全工作。
(4) 阀芯关闭即阀杆反向运动时,U形密封圈应力云图及最大接触应力随速度和摩擦因数变化的规律如图9和图10分别所示。
从图10可见:当阀杆相做反向运动时,密封圈最大应力即为接触应力,发生在密封圈内唇口,且运动速度对应力大小的影响显著,而摩擦因数对接触应力的影响较小。当速度达到0.33 m/s时接触应力开始急剧增大,达到150 MPa,可以判定此时已经超出橡胶材料的撕裂强度。
(5) 通过对阀杆的振动模态分析,得知阀杆在运动时不可避免会产生径向摆动,在此等效为阀杆两端受到垂直转矩的作用,即在模型上对阀杆两端面单元施加水平力载荷,同时考虑阀杆正向运动,得到在正常速度和压力下密封圈应力分布如图11所示,密封圈最大应力变化规律如图12所示。

图9 阀杆反向运动时密封圈应力云图(f=0.1, v=−0.03 m/s, p=32 MPa)Fig.9 U-ring seal’s stress nephogram of valve stem move reverse
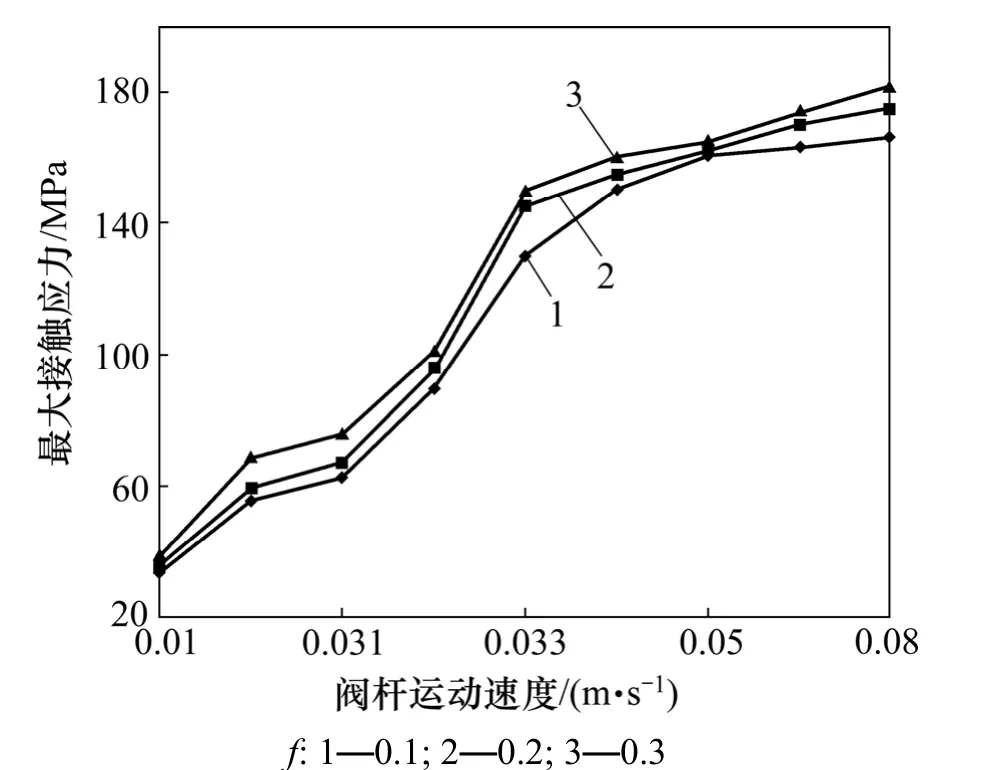
图10 阀杆反向运动时最大接触应力随速度变化曲线(p=32 MPa)Fig.10 Max contact stress curve of U-ring seal with speed changes during reverse movement
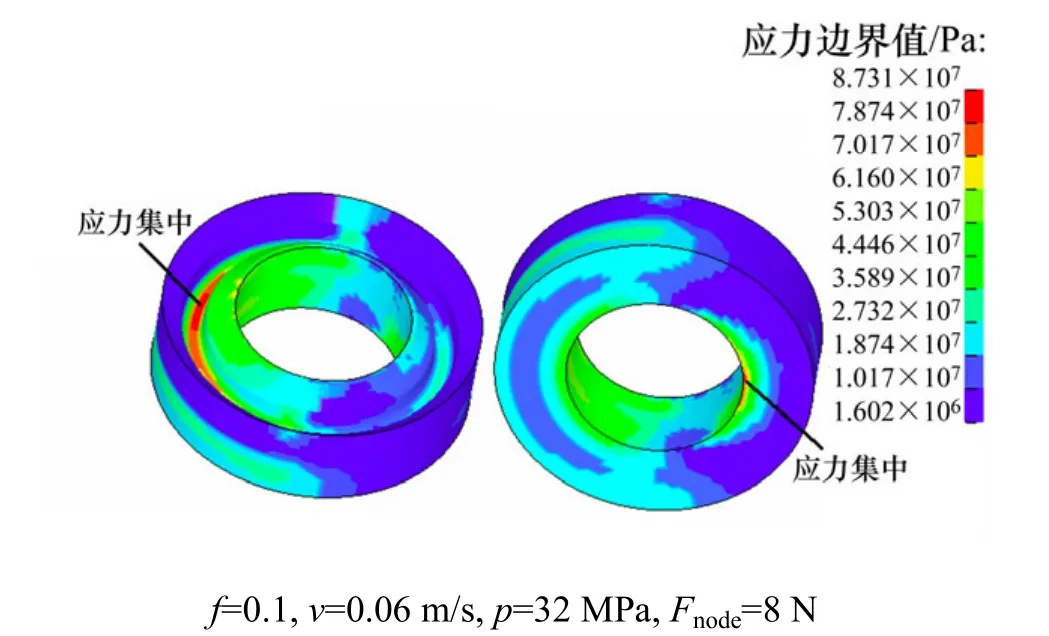
图11 阀杆受水平力作用时密封圈应力云图Fig.11 Stress nephogram of U-ring seal under horizontal force
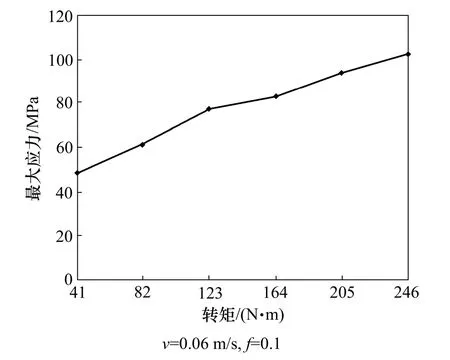
图12 最大应力随转矩变化曲线Fig.12 Max stress curve of U-ring seals with torque changes
从图12可见:密封圈所受最大应力与施加的外部载荷成近似线性变化。当节点载荷为8 N,水平合力为3 328 N,转矩为165 N·m时,最大应力达到87.3 MPa,位于底孔边缘,此时密封圈可能处于失效边界状态;若继续增大节点载荷到10 N时,密封圈与阀杆之间将出现明显间隙。
3 密封失效特征对比
已有研究表明:U型密封圈在密封圈沟槽底部、内唇口以及底孔边缘会出现应力集中,是最可能发生失效的部位,主要失效形式可能为密封圈撕裂破坏、龟裂及出现接触间隙等。由于实际使用的密封圈材质为丁腈夹布橡胶,其强度较纯橡胶得到一定提高。
在实际生产中,密封圈出现的失效特征如图 13所示。从图13可见:其密封损坏和撕裂的位置主要分布在密封圈内槽和内唇口,此特征与仿真结果一致。

图13 密封圈失效特征Fig.13 Failure characteristics of U-ring seals
另外,阀杆的导套在工作中会出现较大变形和磨损,一般2月得更换1次,表明阀杆在实际生产中会产生较大的径向摆动力,在工作过程中会发生振动和扭转变形,从而增大密封圈的径向受力和变形,可引起密封接触出现间隙和应力集中。
4 结论
(1) 基于LS-DYNA软件和Mooney-Rivlin橡胶材料模型进行了U形橡胶密封圈的三维非线性接触动力学分析,结果表明本方法有效可行。
(2) 阀杆静止时密封圈最大应力出现在沟槽底部且比介质压力大8~10 MPa;阀杆在正向运动时,密封圈处于安全状态,其最大应力受摩擦因数影响明显,受运动速度影响较小;阀杆反向运动时,密封圈最大应力出现在内唇口顶部且受阀杆速度的影响显著,当速度大于0.33 m/s时急剧增大;当阀杆径向受力时,密封圈最大应力出现在沟槽和底孔边缘,应力与水平力近似成正比关系。
(3) U形密封圈的沟槽、内唇口及底孔边缘是发生强度失效的主要部位,系统液压冲击、阀杆反向运动速度和径向受力是引起U形橡胶密封圈发生失效的主要因素。可通过降低阀杆运动速度,提高阀杆及其导套的刚度、减小系统液压冲击等措施提高密封圈的使用寿命。
[1] Stanistaw, Stupkiewicz, ArturMarciniszyn.Elastohydrodynamic lubrication and finite conguration changes in reciprocating elastomeric seals[J].Tribology International, 2009, 42(5):615−627.
[2] 陈国定, Haiser H, Haas W, 等.O形密封圈的有限元力学分析[J].机械科学与技术, 2000, 19(5): 740−744.CHEN Guoding, Haiser H, Haas W, et al.Analysis of elastomeric O-ring seals using the finite element method[J].Mechanical Science and Technology, 2000, 19(5): 740−744.
[3] 刘溪涓, 刘承宗, 林钧毅, 等.一种含超弹性接触问题的密封结构的有限元求解方法[J].中国机械工程, 2001, 12(1):1211−1213.LIU Xijuan, LIU Chengzong, LIN Junyi, et al.JIANG Shouwei.A new finite element analysis method of the sealing structure with axial symmetric hyper elastic contact problem[J].China Mechanical Engineering, 2001, 12(11): 1211−1213.
[4] Kim C K, Shim W J.Analysis of contact force and thermal behaviour of lip seals[J].Tribology International, 1996, 30(2):113−119.
[5] Maoui A, Hajjam M, Bonneau D.Effect of 3D lip deformations on elastohydrodynamic lip seals behavior[J].Tribology International, 2008, 41(9): 901−907.
[6] XIE Jian, TIAN Gui, CHEN Jun.Finite element analysis of the rubber sealing Yx-ring in hydraulic cylinder[C]//International Conference on Measuring Technology and Mechatronics Automation.Xi’an: Xi’an Res Inst of Hi-Tech, China, 2009:806−809.
[7] 侯珍秀, 余志洋, 刘云猛, 等.X形丁腈橡胶密封件的有限元分析[J].宇航材料工艺, 2007, 37(6): 15−20.HOU Zhenxiu, YU Zhiyang, LIU Yunmeng, et al.Finite element analysis for nitrile rubber X-ring seal structure[J].Aerospace Materials & Technology, 2007, 37(6): 15−20.
[8] 陈敏, 汤文成, 张逸芳, 等.阀门密封结构中超弹性接触问题的有限元分析[J].中国机械工程, 2007, 18(15): 1773−1775.CHEN Min, TANG Wencheng, ZHANG Yifang, et al.Finite element analysis of hyperelastic contact problem in valve sealing structure[J].China Mechanical Engineering, 2007, 18(15):1773−1775.
[9] 张春宇.50 MN锻造水压机进水阀及电液控制系统仿真[D].燕山: 燕山大学机电工程学院, 2007: 5−7.ZHANG Chunyu.Simulation study on inlet valve and electro-hydraulic control system of 50 MN hydraulic forging press[D].Yanshan: Yanshan University.School of Mechanical and Electronic Engineering.2007: 5−7.
[10] 刘江明.300 MN模锻水压机水路系统液压冲击研究 [D].长沙: 中南大学机电工程学院, 2010: 6−7.LIU Jiangming.Analysis on hydraulic impact in hydraulic system of 300 MN die forging hydraulic press[D].Changsha:Central South University.School of Mechanical and Electronic Engineer, 2010: 6−7.
[11] 桑园, 张秋翔, 蔡纪宁, 等.滑移式机械密封的动态辅助密封圈性能研究[J].润滑与密封, 2006, 184(12): 95−98.SANG Yuan, ZHANG Qiuxiang, CAI Jining, et al.Study on the dynamic auxiliary seal ring of pusher type mechanical seal[J].Lubrication Engineering, 2006, 184(12): 95−98.
[12] 何涛.ANSYS10.0/LS-DYNA非线性有限元分析实例指导教程[M].北京: 机械工业出版社, 2007: 111−122.HE Tao.ANSYS10.0/LS-DYNA instances of non-linear finite element analysis tutorial[M].Beijing: China Machine Press,2007: 111−122.
[13] 黄建龙, 解广娟, 刘正伟.基于Mooney-Rivlin模型和Yeoh模型的超弹性橡胶材料有限元分析[J].橡胶工业, 2008, 55(8):467−471.HUANG Jianlong, XIE Guangjuan, LIU Zhengwei.FEA of hyperelastic rubber material based on Mooney-Rivlin model and Yeoh model[J].China Rubber Industry, 2008, 55(8): 467−471.
[14] 郑明军, 王文静, 陈政南, 等.橡胶 Mooney-Rivlin模型力学性能常数的确定[J].橡胶工业, 2003, 50(8): 462−465.ZHEN Mingjun, WANG Wenjing, CHEN Zhengnan, et al.Determination for mechanical constants of rubber Mooney-Rivlin model[J].Rubber Industry, 2003, 50(8): 462−465.
[15] 彭兵, 林生义, 向宇.提高丁腈橡胶夹布密封件使用性能研究[J].润滑与密封, 2007, 32(5): 174−175.PENG Bing, LIN Shengyi, XIANG Yu.Nitrile rubber fabric to improve performance of seals[J].Lubrication Engineering, 2007,32(5): 174−175.

