可交换矩阵的性质及应用

孟献青，张 英，乔世东

（山西大同大学数学与计算机科学学院，山西大同037009）

由矩阵论知，矩阵的乘法不满足交换律，即当矩阵AB 有意义时，矩阵BA 未必有意义，即使AB，BA 都有意义，它们也未必相等。但是在某些特殊情况下，矩阵的乘法也是满足交换律的，如果矩阵A，B 满足AB＝BA，则称矩阵A，B 是可交换的。可交换矩阵是矩阵理论中一类重要的矩阵，在文献[1-5]的基础上罗列出可交换矩阵的一些性质，及这些性质在解题中的应用。

1 性质

性质1设矩阵A，B 可交换，且

则

证明：设

由AB＝BA 得，

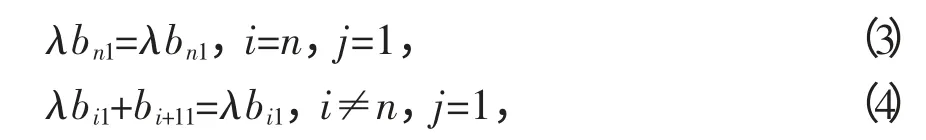
由（4）得：bi+11＝0，即

由（2）得：bnj-1＝0，即

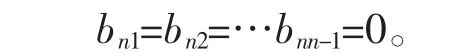
由（1）得：

令j＝2 得：bi+12＝bi1＝0，i≠1，

将（5）代入（6）得bij＝0，i＞j。

令b11＝b1，由（6）得bii＝b1，

令b12＝b2，由（6）得，

所以

性质2若矩阵A， B 可交换， 则对任一多项式f（λ），有f（A）B＝Bf（A）。

性质3[1]设A， B 为n 阶可交换方阵，且A， B 都可对角化， 则存在可逆矩阵P， 使P-1AP 与P-1BP 同时为对角阵。

证明 由于A 可对角化，从而存在可逆矩阵T，使

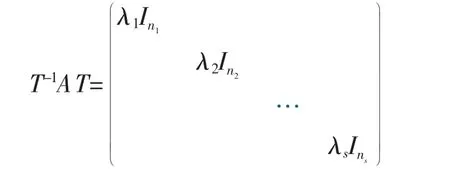
其中λ1，λ2，…，λs互不相同，且

由AB＝BA，得，

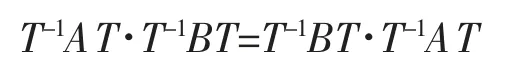
所以

为准对角矩阵，其中Bk为nk×nk矩阵。由于B 可对角化，则它的初等因子都是一次因式，所以Bk的初等因子也是一次因式。 故存在可逆矩阵Rk，k＝1，2，…，s 使得R-1kBkRk为对角阵。令

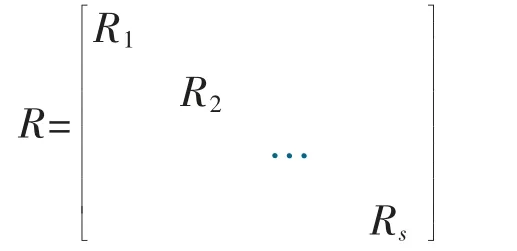
则

为对角阵。

再令Ρ＝ΤR，则Ρ 可逆，且

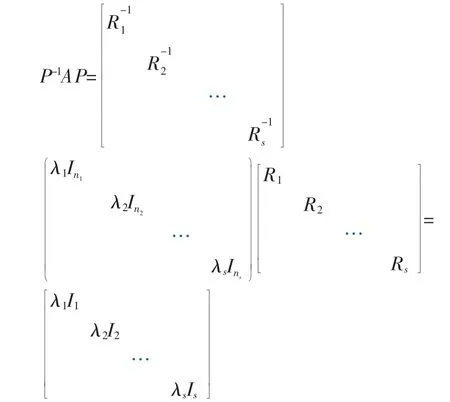
为对角阵。

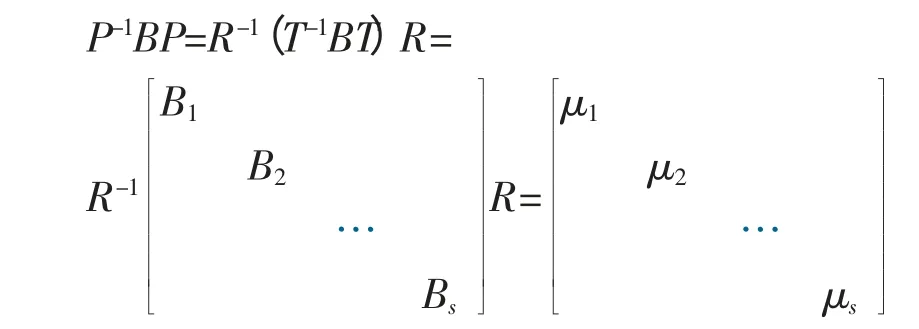
为对角阵。证毕

性质4[3]设A，B 为n 阶可交换方阵， 则A，B同时相似于三角形矩阵。

性质5[4]若

且AB＝BA，则B 是A 的多项式。

2 应用

例1设A，B 是实正定矩阵，证明AB 是正定矩阵的充要条件是AB 可交换。

证明（必要性）因为A，B 是实正定矩阵，从而是实对称矩阵，所以AB＝（AB）′＝B′A′＝BA。（充分性）因为A，B 是实正定矩阵且AB＝BA，所以（AB）′＝B′A′＝BA＝AB，即AB 是实对称矩阵。又因为A 与B 都是正定矩阵，从而都可以对角化，由性质3 知，存在可逆矩阵P，使P-1AP 与P-1BP 同时为对角阵，不妨设

所以

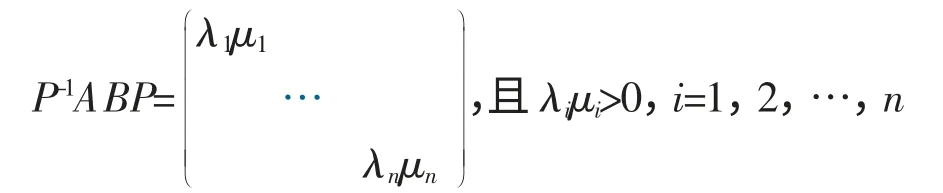
从而AB 为正定矩阵。

例2若A 相似于若当块

则与A 可交换的矩阵是A 的多项式。

证明 由题设知存在可逆矩阵P 使P-1AP＝J，即A ＝PJP-1，设B 与A 可交换，则PJP-1B ＝BPJP-1，从而有J·P-1BP ＝P-1BP·J，故P-1BP 与J 可交换。 由性质5 知，P-1BP 是J 的多项式，即f（J）＝P-1BP。设多项式f（λ）＝a0λn+a1λn-1+…an-1λ+an，则B＝Pf（J）P-1＝f（PJP-1）＝f（A）。

例3设A，B 为n 阶可交换矩阵，且Ak＝0，k≥1，证明｜A+B｜＝｜B｜。

证明 因AB＝BA，由性质4 知，存在可逆矩阵P 使

其中λi是A 的特征根，μi是B 的特征根，1≤i ≤n由于Ak＝0，故λi＝0，1≤i≤n。从而P－1（A+B）P 对角线上的元素与P－1BP 对角线上的元素相同，于是｜A+B｜＝｜P－1（A+B）P｜＝｜P－1BP｜＝｜B｜。

例4设A，B 为n 阶可交换矩阵，AB ＝BA。证明A，B 同时相似于三角形矩阵。

证明 对A，B 的阶数n 用归纳法。

n ＝1 时结论显然成立，设n ＜k 时，结论成立，我们证明n ＝k 时结论亦成立。

A，B 有公共的特征向量X1，设AX1＝λX1，BX1＝μX1，设X1，X2，…，Xn是n 维线性空间的一组基，在此基下A，B 对应的线性变换A，B 的矩阵分别为

于是Q－1AQ ＝A1，Q－1BQ ＝B1，由AB ＝BA 有

即

由归纳假设Α2，B2同时相似于三角形，即存在非奇异矩阵P2使A2P2，P－12B2P2同时为三角形阵。

令

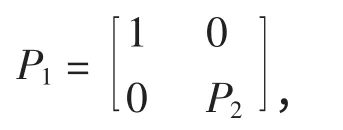
则

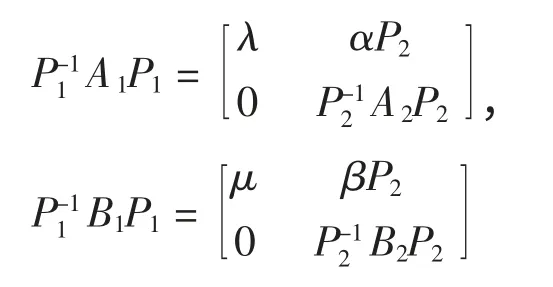
是三角形矩阵。

令P ＝QP1，则P－1AP 与P－1BP 是三角形矩阵。

[1]钱吉林. 高等代数题解精粹[M]. 北京： 中央名族大学出版社， 2002.

[2]曾梅兰. 线性变换及阵矩可交换的性质与应用[J]. 孝感学院学报，2006， 26(3)： 44 - 46.

[3]布合力且木·阿不都热合木. 论可交换矩阵的一些性质[J]. 和田师范专科学校学报，2008， 28(5)： 201 - 202.

[4]黎伯堂， 刘桂真.高等代数解题技巧与方法[M]. 济南：山东科学技术出版社， 2002.

[5]刘小川， 何美.幂等矩阵与秩幂等矩阵的充要条件[J]. 山西大同大学学报：自然科学版， 2011，27(1)：14－16.