一类亚纯函数差分的零点估计

金 瑾

（毕节学院数学系，贵州毕节551700）

1 主要结论

亚纯函数Nevanlinna 理论的基本慨念和标准记 号[1-15]， 用σ（f）表 示函 数f（z）的 级， 用λ（f）和分别表示函数f（z）的零点收敛指数和不同零点收敛指数， 用λ（r，1／f）表示极点收敛指数， 用n（r，f）和n（r，1／f）分别表示函数f（z）在半径为r 的圆内极点和零点的个数， 用μ（f）表示函数f（z）的下级， 用T（r，f）表示函数f（z）的特征函数。

文章[1-2]聚焦于复域差分函数和Nevanlinna 理论的差分模拟， Bergeiler 和Langley 在文献[1]中首先研究了差分Δf（z）和Δf（z）／f（z）的零点存在性，得到了许多深刻且有意义的结果。

定 理A[1]设δ0∈（0，1 ／ 2）， 函 数f（z）是 级σ（f）＝σ＜σ0+1／2＜1 的超越整函数， 则

有无穷多个零点。

定理B[1]设函数f（z）是超越亚纯函数， 下级μ（z）＜1， 设c∈C-｛0｝使得f（z）最多有有限个极点zj，zs满足zj-zs＝c， 则函数h（z）＝f（z+c）-f（z）有无穷多个零点。

定理C[2-4]设函数f（z）是超越亚纯函数且

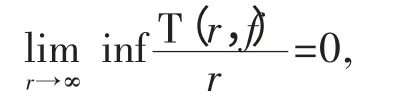
则f′（z）有无穷多个不动点。

定理D[5]设函数f（z）是超越亚纯函数， 级σ（f）＝σ＜1， c1，c2∈C-｛0｝， 且c1+c2≠0， 则函数

有无穷多个零点且满足λ（g）＝σ（g）＝σ。

特别地， 如果f（z）最多有有限个零点zj满足

则函数

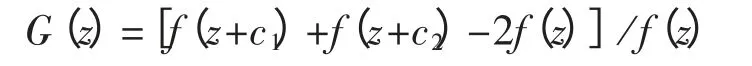
满足λ（G）＝σ（G）＝σ。

定理E[5]设函数f（z）是超越亚纯函数， 级σ（f）＝σ＜1， c1，c2∈C-｛0｝， 且c1+c2≠0， 则函数

有无穷多个零点且满足λ（g）＝σ（g）＝σ。特别地，如果f（z）最多有有限个零点zj，zs满足zj-zs＝c1或c2， 则函数

满足λ（G）＝σ（G）＝σ。

本文在这些结果的基础上得到下面结果。

定理 设函数f（z）是超越亚纯函数， 级σ（f）＝σ＜1， c1，c2， c3∈C-｛0｝，且c1，c2， c3≠0， 则函数

有无穷多个零点且满足λ（g）＝σ（g）＝σ。特别地，如果函数f（z）最多有有限个零点

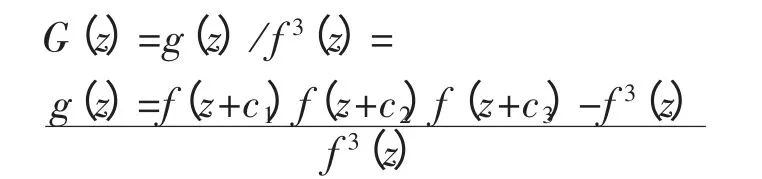
zj，zs满足zj- zs＝c1或c2或c3， 则函数满足λ（G）＝σ（G）＝σ。

2 引理及证明

根据文献[6]， ε-集E 是可数个不包含原点的开圆盘的并集。如果E 是一个ε-集， 则对r≥1 并使圆S（0，r）与E 相交的r 值集有有限对数测度和有限线测度，对几乎所有实数θ，集E 与射线arg z＝θ 相交点是有界的。

引理1[1]设函数f（z）是超越亚纯函数， 级σ（f）＝σ＜1， h＞0， 则存在一个ε-集E 满足

对满足｜c｜≤h 的c 一致成立。

引理2 设函数f（z）是超越亚纯函数， 级σ（f）＝σ＜1， c1， c2，c3∈C-｛0｝，且c1， c2，c3≠0， 则

是超越的。

证明假设

是一个有理函数， 即

其中R(z)是一个有理函数， 由已知和引理1 知， 存在一个ε-集E， 使得当｜z｜＝r 充分大， z∈C-E 时有

将(1) (2) (3)三个式子的左右两边分别相乘得

整理(4)式并由(1)(2)(3)得

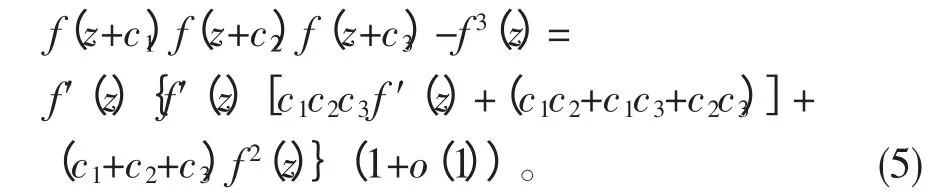
所以

即

g（z）＝f（z+c1）f（z+c2）f（z+c3）-f3（z）是超越的。

3 定理的证明

因为函数f（z）是超越亚纯函数，故由引理2 可知

是超越亚纯函数， 这样就有σ（g）＜σ（f）。由σ（g）＜σ（f）可知， 存在实数δ 和α 满足

再由已知和引理1 可知存在ε-集E，当｜z｜＝r 充分大，z∈C-E 时有(1)(2)(3)成立。令f（z）＝f0（z）／d（z）， 其中d（z）是由函数f（z）的所有极点形成的多项式， f0（z）是超越函数且满足σ（f）＝σ（f0）＝σ＜1， 由Wiman-Valiron 理论[6-7]可知， 存在子集F⊂（1，∞）具有有限对数测度满足： 对充分大的r∉F， 对所有满足｜z｜＝r和｜f0（z）｜＝M（r，f0）的z 有

其 中， v（r）是f0（z）的 中 心 指 标， 由(8)和f（z）＝f0（z）/d（z）， 使用文献[8]中的方法可知， 对所有满足｜z｜＝r 和｜f0（z）｜＝M（r，f0）的z 有

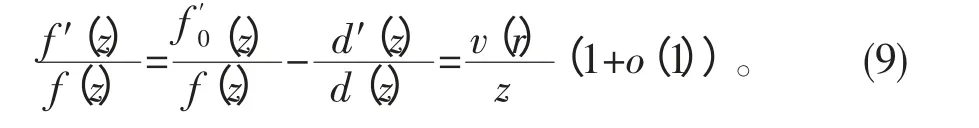
令F1＝｛｜z｜：z∈E｝， 因E 是ε-集， 故F1具有有限对数测度。由引理2 的证明过程知

所以由(9)和(10)式得

其中， v（r）是f（z）的中心指标， z 满足｜z｜＝r∉[0，1]UFUF1和｜f（z）｜＝M（r，f）。由(7)式存在一序列｛rn｝（rn→∞）满足任意的ε（0＜ε＜1-σ）有

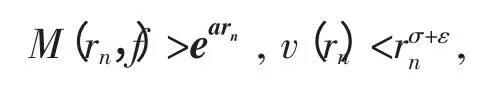
由(12)式和c1，c2，c3∈C-｛0｝， 及已知c1+ c2+ c3≠0可知， (11)式的两边矛盾， 所以σ（g）＝σ（f）。 故

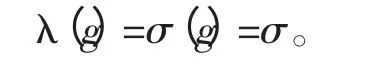
另外， 由

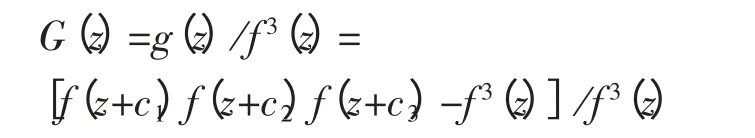
和已知函数f（z）是超越亚纯函数可知： 如果z0是G（z）的零点， 则z0也是g（z）的零点; 如果z0是g（z）的零点且不是G（z）的零点， 则z0一定是f（z）的零点。这样， 就有

或

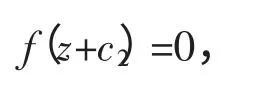
或

由定理条件， f（z）仅有有限个这样的零点z0， 因而有

所以，

[1]Bergweiler W，Langley J K. Zeros of differences of meromorphic functions [J]. Math Proc Camb Phil Soc， 2007(142)： 133-147.

[2]Bergweiler W， Eremenko A. On the singularities of the inverse to a meromorphic function of finite order [J]. Rev Math Iberoamericana， 1995(11)： 355 - 373.

[4]Hinchliffe J D. The Bergweiler - Eremenko theorem for finite lower order [J]. Results Math， 2003（43）： 121 - 128.

[5]陈宗煊， 孙光镐. 亚纯函数差分的零点估计[J]. 中国科学， 2010， 40(1)： 53 - 64.

[6]Hayman W K. Slowy growing integral and subharmonic functions [J]. Comment Math Helv， 1960（34）： 75 - 84.

[7]Lainne I. Nevanlinna theory and complex differential equations [M]. Berlin： W de Gruyter， 1993.

[8]Chen Z X， Shon K H. On sbnormal solutions of second order linear periodic differential equations[J]. Sci China Ser A， 2007（50）： 786-800.

[9]金瑾. 复方程f＂+Af＝0 的解的零点充满圆[J]. 数学进展， 2005(5)： 609 - 613.

[10]金瑾. 高阶整函数系数线性微分方程的解及其解的导数的不动点[J]. 数学研究与评论， 2007， 27(4)： 107 - 113.

[11]金瑾. 高阶线性微分方程解的二阶导数的不动点[J]. 数学理论与应用， 2007， 27(4)： 107 - 113.

[12]金瑾. 一类微分方程的解及其解的导数与不动点的关系[J]. 数学实践与认识， 2011，41(22)： 185 - 190.

[13]金瑾. 高阶齐次线性微分方程解的超级的角域分布[J]. 数学实践与认识， 2008，38(12)： 178 - 187.

[14]金瑾. 关于亚纯函数φ(z)fn(z)f(k)(z)的值分布[J]. 纯粹数学与应用数学， 2012， 28(6)： 1 - 8.

[15]Jin jin.The fixed point and hyper order of solutions of higher order nonhomogeneous linear differential equations with meromorphic function coeffcents [J]. Mechanicaland Aerospace Engineering，ICMAE2011： 3297 - 3300.