用变分方法计算天文折射
杨步恩
(大连理工大学物理与光电学院 辽宁 大连 116024)
1 引言
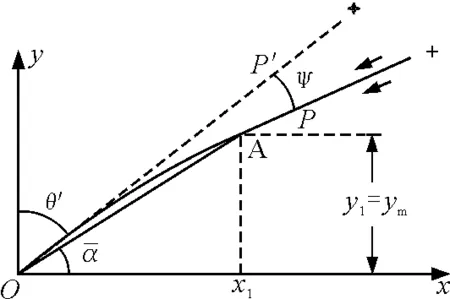
在地面上观察恒星的角位置,因为地球大气密度随高度变化的不均匀性,使来自遥远恒星的平行光不断折射而弯曲,且改变了平行光原传播方向.因此,观察者所看到的恒星,不在恒星的原位置,如图1所示.
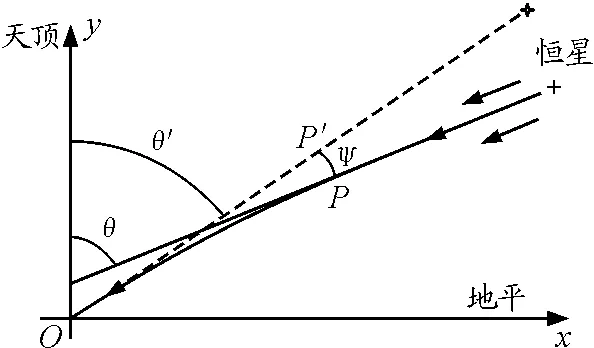
图1 天文折射
在O点观测恒星,其实是在光线的切线方向上测量恒星像点P′的位置,然而该点已经偏离了恒星的实际位置P.为此,观察者要知道,恒星的视位置确定后,偏离真位置方向的角度ψ,通常称之天文折射(即大气折射)
ψ=θ-θ′
(1)
等于恒星的视天顶角θ′与真天顶角θ相减.此式还可以用视角高α′与真角高α之差来表示
ψ=α′-α
(2)
式中,α与θ是互为余角.
从历史的角度看[1],大气折射理论,首先由天文学家卡西尼创立.之后,牛顿、布拉得雷、拉普拉斯和贝塞尔等著名科学家,对大气折射都进行过研究.但是,关于大气质量分布都假定:大气是中心对称分层的,每个球面层与地球同心,而且密度均质.因为地球的半径很大,所以靠近地面大气的逐个球面层,在有限范围内可看成互相平行的平面层.
在此大气模型的假设下,天文学家推出大气折射ψ数学式,也是至今普遍应用的公式[2].
根据几何光学的斯耐尔(Snell)折射定理
rnsinθ=(R0+y)nsinθ=R0n0sinθ′
(3)
式中,R0是地球半径,y是球面层离地面高度,n是该球面层折射率,n0是地面空气折射率,而θ′是视天顶角.由此式推出大气折射为
ψ=(n0-1)tanθ′
(4)
其中,n0-1=293×10-6.
然而,该式在天顶角θ′不大于70°时与实际尚能符合.但是,如果恒星接近地平面,且天顶角大于70°时,那么,式(4)的计算值与实际就不大相符了.今天看来,大气折射ψ依然是尚未解决的问题.
为此,该文提出不同于Snell定理的计算法,而是引入Fermat最短时间原理,通过求光曲线的入射点和出射点的切线斜率计算ψ角.对那些视天顶角θ′>70°的恒星,能给出较正确结果.
下面阐明,在大气分层假定的框架下,再引入近地大气状态是等温的,其质量分布遵循重力场的气体分子数的玻尔兹曼分布律.如此,大气密度随高度y变化的表达式是
ρ(y)=ρ0e-z
(5)
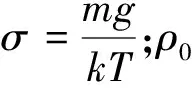
2 大气折射率随高度变化的表达式
由光的电磁理论阐明的Lorentz-Lorenz公式,气体折射率与密度的关系是[3]
(6)
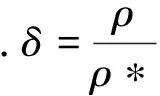
(7)
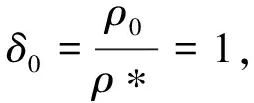
(8)
因此,得地面大气折射率为
n0=1+μ0=1+293×10-6
如果将式(5)代入式(7),那么,大气折射率随高度y变化的表达式为
n(y)=1+μ0e-z
(9)
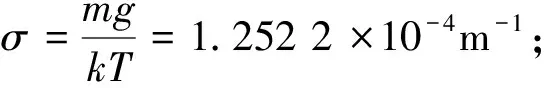
k=1.38×10-23J/K,T= 273 K.
3 大气的“光学厚度”
由式(9)知道,当y→∞时,n(∞)=1.此结果,在我们看来,仅有理论意义.因为y的取值已经超出了玻尔兹曼分布律的适用范围(y≪R0).同时,也与通常估计大气折射率n(y),在离地面有限高度处取n=1的假设相悖.因此,为了调和二者的不一致.引进大气“光学厚度”物理量.办法是将折射率n(y)展开为幂级数,仅取前面几项之和表示,即
(10)
这里,函数n(y)的边界条件是
(11)
因为y=ym处,大气的n(ym)=1,所以将此条件代入式(10),得代数方程
(12)
该方程的最高次幂为奇数时,有一正实数根为z1,因此得大气“光学厚度”为
(13)
讨论三种特殊情形:
(1)令p= 0,1.则方程式(12)为
z-1=0
该方程的实数根为z1=1,所以大气光学厚度为
(14)
该厚度ym1与估计等密大气厚度为8 km相吻合.
(2)令p= 0,1,2,3.则方程式(12)为三次方程
z3-3z2+6z-6=0
此方程的正实数根z1≈1.596,所以光学厚度
(15)
(3)令p= 0,1,2,3,4,5.式(12)为五次方程
z5-5z4+20z3-60z2+120z-120=0
该方程的正实数根z1≈2.1806.因此,光学厚度
(16)
观测表明上述三种光学厚度均在大气对流层顶18 km以下.除此,光学厚度以内大气的平均折射率为
(17)
将式(10)代入式(17),在三种光学厚度情形下,大气折射率的平均值为
(18)
4 大气折射的零级近似ψ0
观测表明大气折射主要是近地大气层的效应,那些天顶距大于75°的恒星,其天文折射为4′至34′,即是有力的证据.
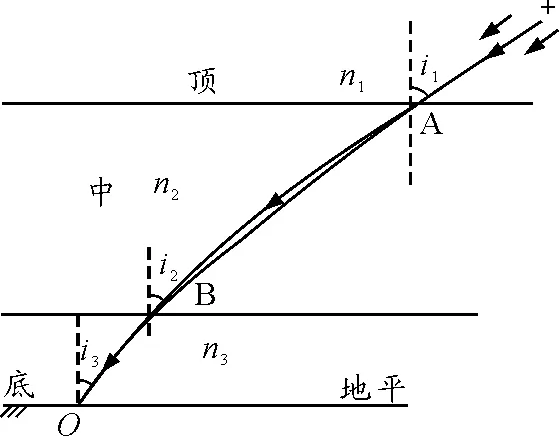
鉴此,根据分层理论,将近地大气按光学性质分为三层.
(1)顶层,在大气光学厚度ym之上,空气折射率近似为1.
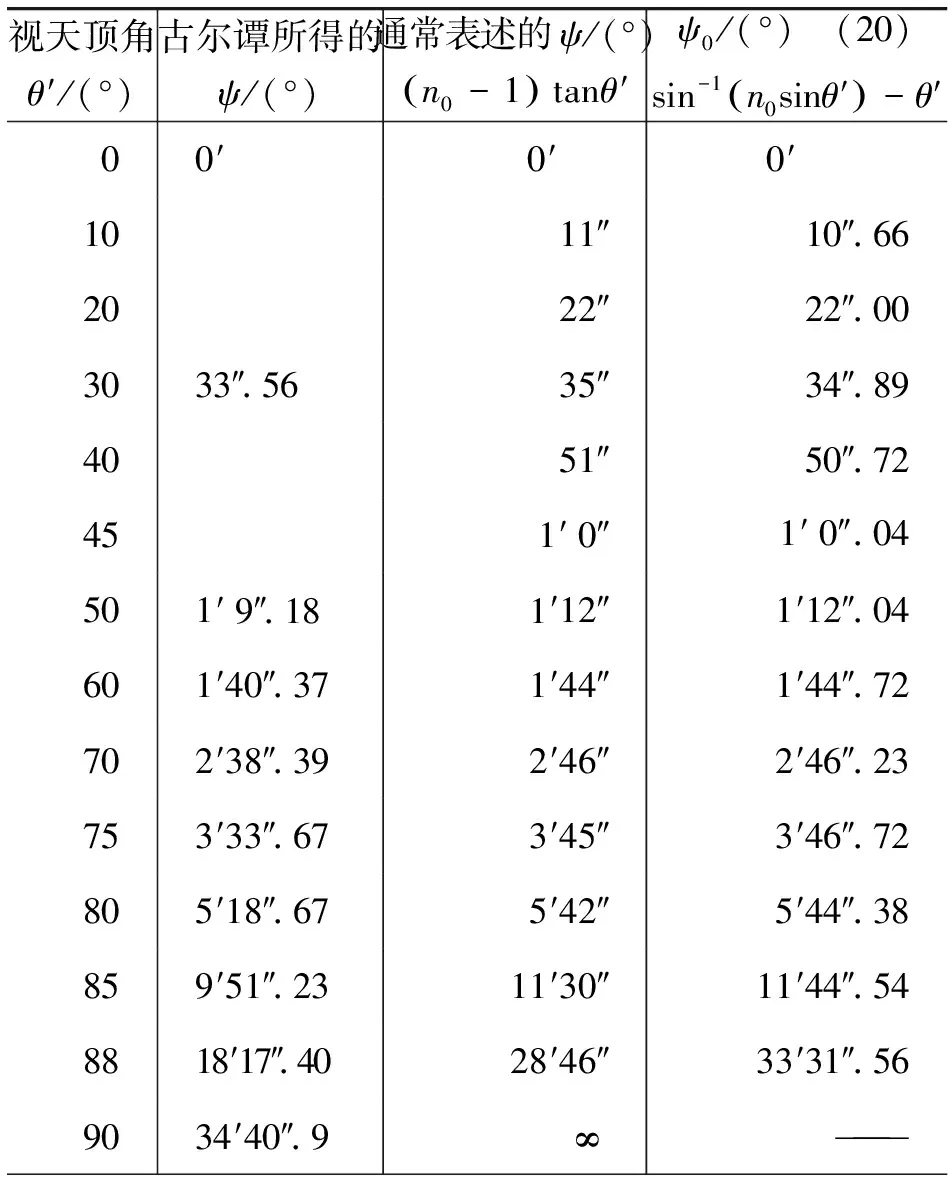
(2)中层,在ym至近地之间,空气折射率n(y)随高度y变化,但是1 (3)底层,近地面空气折射率为n0几乎不变. 图2 近地大气的光学分层 根据几何光学的Snell折射定理,光在上述平行平面层大气模型传播,该定理蜕化为形式 n1sini1=n2sini2=n3sini3 对此式作变换 以及 则得 (19) 由此,得到以θ′表示的大气折射零级近似为 ψ0=sin-1(>n0sinθ′)-θ′ (20) 计算表明ψ0的数值与通常表示天文折射ψ公式(4)数值几乎相同,如表1所示. 表1 天文折射ψ0随天顶角的变化[2] 此前的讨论,依然是应用大气分层理论来计算天文折射ψ.虽然引入光学分层和光学厚度的概念.但是,这没有超越大气分层的范畴. 欲得到高精度ψ的数值,必须从普遍的原理出发,并且以新的方法去探索达到此目标的途径.几何光学中有一条比Snell折射定理更普遍的原理,即Fermat最短时间原理,以此取代折射定理,可能是实现此目标的捷径. 下面,从此原理出发,推导等温大气光的极值曲线函数.Fermat原理的数学式是 (21) (22) 该式被积函数为 于是,由式(22)推出微分方程 (23) 光的极值曲线y(x)的边界条件是 y(0)=0y(x1)=y1 (24) y0(x)=kx (25) 在此情况下,方程(23)以近似形式表示为 (26) 图3 重力场等温大气光曲线 微分方程式(26)的偏导数为 式中,变量z0=σy0(x)=σkx. k(>1+μ0e-z0)δy′-(>1+k2)μ0σδy=0 (27) 对式(27)积分,得δy函数为 δy=c0(>1+μ0e-z0)-k′=c0n(>kx)-k′ (28) y(x)=δy+c1=c0[n(>kx)]-k′+c1 (29) 积分常数c0和c1,由边界条件式(24)来确定 (30) 将式(30)代入式(29),则得光的极值曲线近似函数为 (31) 为简化计算,引进光学厚度ym,将式(31)的折射率n(y)随高度y递减的形式表达为线性关系 n(y)=n0(1-βy) (32) (33) 式中,y=y0(x)=kx,y1=kx1. (34) 其中,θ′是恒星的视天顶距. 前面表述光曲线函数(33),还可以将折射率(32)直接代入变分原理(21),应用“参考线法”求积分而得相同的结果. 对光曲线函数式(33)求一阶导数,得切线斜率 (35) 式中,y0(x)=kx,y1=kx1. 于是,由式(35)得,光曲线在O点的切线斜率为 (36) 同理,在A点光线的切线斜率为 (37) 式中,α′是恒星的视角高,而α是其真角高. 为了算出天文折射角ψ1,先计算式(36)和式(37)的两式之差,以及两式之积 tanα′-tanα= k(k′+1)βy1 (38) tanα′tanα= k2[1+(k′+1)βy1] (39) 将式(38)和式(39)代入三角恒等式,得到 (40) (41) 此式,即是参考线斜率k表述的天文折射. 第一步,为检验ψ1计算后的数值是否正确?首先算出ψ0,由式(20)得大气折射零级近似为 ψ0=sin-1(n0sinθ′)-θ′ 将θ′=65°代入式中,得ψ0=2′9″.69. 第二步,计算参考线的斜率k:由式(19)和式(34)得 第三步,将k的数值代入式(41),得 同理,重复上述步骤,计算其他恒星天文折射ψ1在不同光学厚度情况下,ψ1随θ′变化的数值,如表2所示. 表2 天文折射ψ1随天顶角的变化 (1)通常表述的天文折射公式为 ψ=(>n0-1)tanθ′ 与根据光学分层推出天文折射零级近似 ψ0=sin-1(n0sinθ′)-θ′ 是等价的,二者的数值几乎相等. (2)根据Fermat原理,用“参考线法”推得等温大气光的极值曲线函数为 n(kx)=1+μ0e-z0 (3)用参考线斜率k表示天文折射 (4)大气光学厚度ym的不同,几乎对ψ1没有影响.当θ′>70°时,ψ1才略有偏差.由此看来,大气折射是近地大气效应.除此,表2给出,θ′=88°恒星,其ψ1=34′20″.48与古尔谭给出θ′~90°,ψ=34′40″.9相当接近,也证实了这一点. 参考文献 1 胡宁生.大气折射.中国大百科全书(天文学),1980(2):42~43 2 J·C·强生.物理气象学.王鹏飞译.北京:科学出版社,1960.24~27 3 杨步恩.光线在湍流大气中作Brown运动的统计解释.大连理工大学学报,1991(5):515~520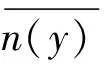
5 重力场等温大气的光曲线函数
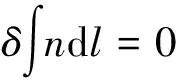
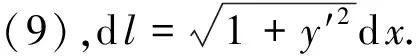

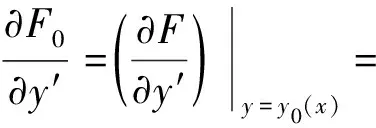
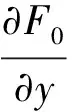
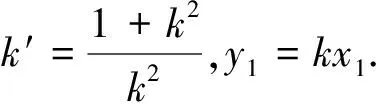
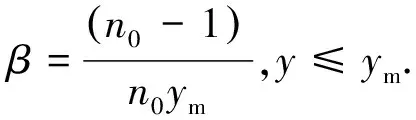

6 参考线斜率k表示的天文折射
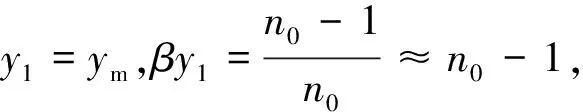
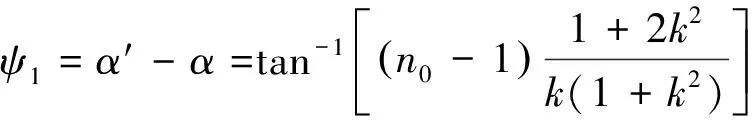
7 天文折射ψ的计算
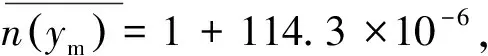
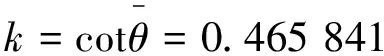
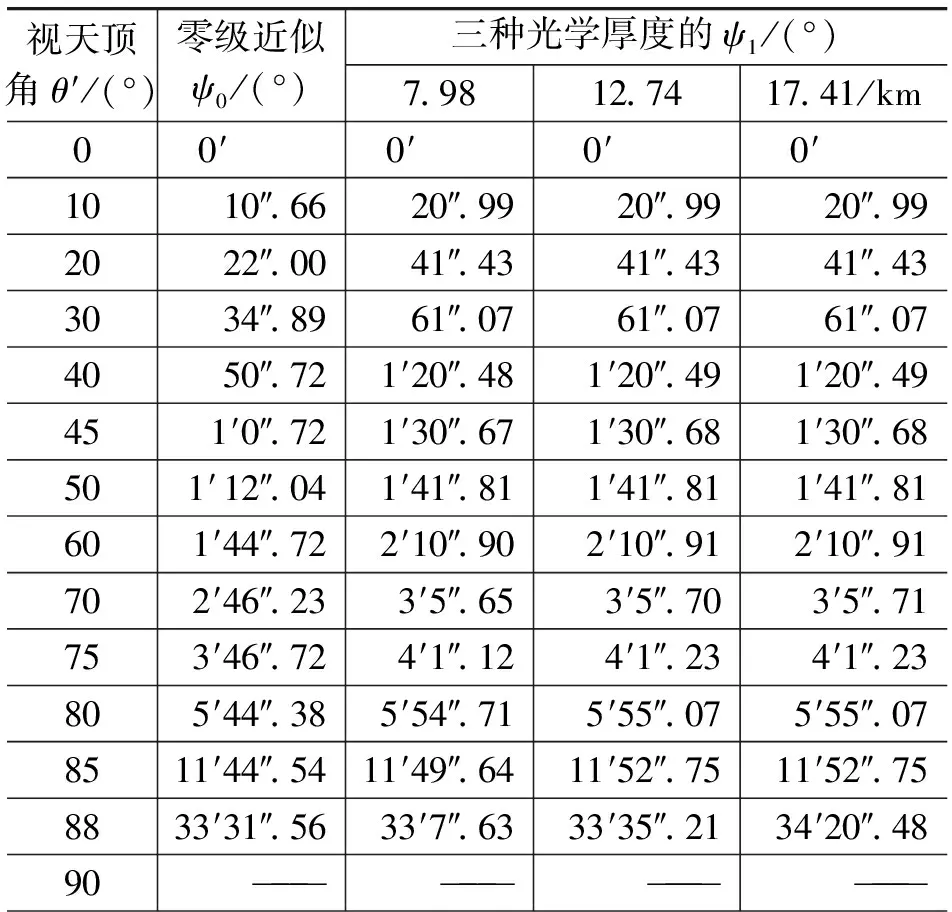
8 结论

