直纹曲面是可展曲面的一个充要条件*
吴 芸,纪永强
(湖州师范学院 理学院,浙江 湖州313000)
微分几何是一门历史悠久的学科,近年来对数学中其它分支的影响越来越深刻,对自然科学中其它学科的影响范围也越来越大.与此同时,这门学科从内容到方法也在不断更新.
由动直线产生的曲面称为直纹曲面,动直线为该直纹曲面的直母线.如柱面、锥面、一条曲线的切线曲面等都是直纹曲面.可展曲面是直纹曲面的一种重要类型,它的研究是经典微分几何必涉及的内容.现在许多课程都用到了可展曲面的基本理论和基本思想方法,而且这方面的资料也很丰富.文献[1]中,利用曲线测地挠率与曲线挠率的关系刻画了直纹曲面是可展曲面.文献[2]中,利用单参数平面族的包络面刻画了直纹曲面是可展曲面.文献[3]中,利用曲面的高斯映射像刻画了直纹曲面是可展曲面.文献[4]中,给出了几个定理,并进行了详细说明.
本文推广文献[4]中的定理3.6.9,得到了直纹曲面是可展曲面的一个充分且必要条件,即:直纹曲面S∶r(u,ν)=ρ(u)+νe(u)是可展曲面的充要条件是:曲面S是它的切平面族的包络面.
设C∶ρ=ρ(u)(u1≤u≤u2)是直纹曲面S上的一条准线,即C与所有直母线相交,设e(u)是过P(ρ(u))点的直母线上的非零矢量,则直纹曲面S的参数方程是:
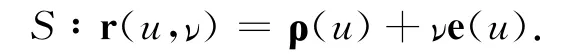
其中u1≤u≤u2,-∞<ν<+∞,u线是与准线C平行的曲线,ν线是直母线.
特别地,当ρ(u)=ρ0是常矢量时,S∶r(u,ν)=ρ0+νe(u)是锥面.当e(u)=e0是常矢量时,S∶r(u,ν)=ρ(u)+νe0是柱面.文献[4]中有如下几个定理:
定理1[4]直纹曲面S∶r=ρ(u)+νe(u)为可展曲面的充要条件是:
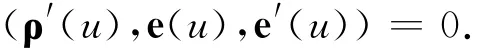
定理2[4]直纹曲面S∶r=ρ(u)+νe(u)为可展曲面的充要条件是:S上的直母线(ν线)是曲率线.
定理3[4]直纹曲面S∶r=ρ(u)+νe(u)为可展曲面的充要条件是:S上任一点的Gauss曲率都为零,即K(u,ν)=0.
定理4[4]直纹曲面S∶r=ρ(u)+νe(u)为可展曲面的充要条件是:或者S是柱面,或者S是锥面,或者S是某一条曲线的切线曲面.
定理5[4]直纹曲面S∶r=ρ(u)+νe(u)为可展曲面的充要条件是:沿准线C∶ν=0,r=ρ(u),S是它的切平面族的包络面.
本文推广上面的定理5,得到如下定理:
定理 直纹曲面S∶r(u,ν)=ρ(u)+νe(u)为可展曲面的充要条件是:曲面S是它的切平面族的包络面.
证明 “⇒”.设直纹曲面S可展,由定理1得:

因为

所以曲面S上任一点M(u,ν)的法矢量为:
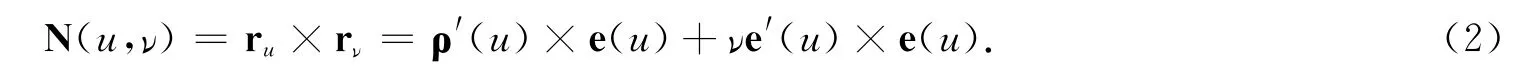
由(1)式知,三矢量ρ′(u),e(u),e′(u)共面,所以

将(3)式代人(2)式得:

曲面S上任一点的切平面的方程是:
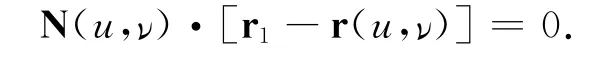
即

即
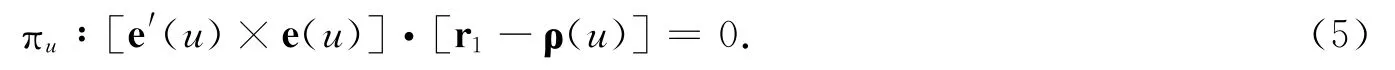
这是单参数为u的切平面方程.现在求切平面族{πu}的包络面,特征线Lu的方程是:
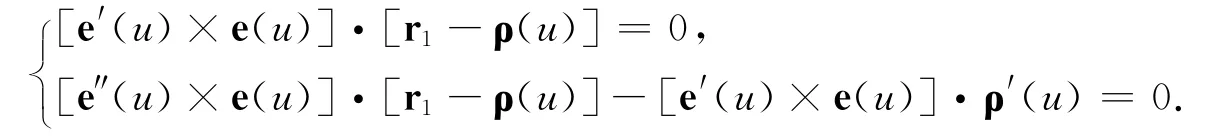
即
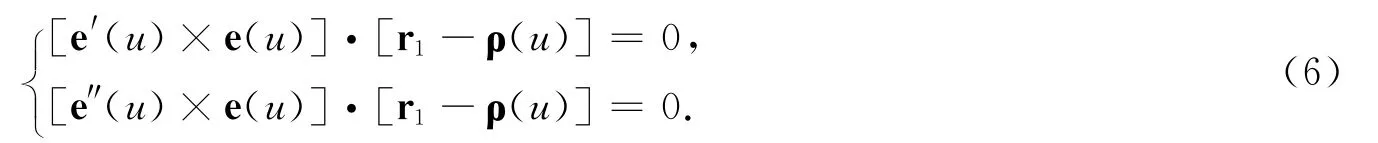
所以平面族{πu}的包络面的准线方程是:

由(5)式知,平面πu的法矢量为:

得特征线Lu的方向矢量为:
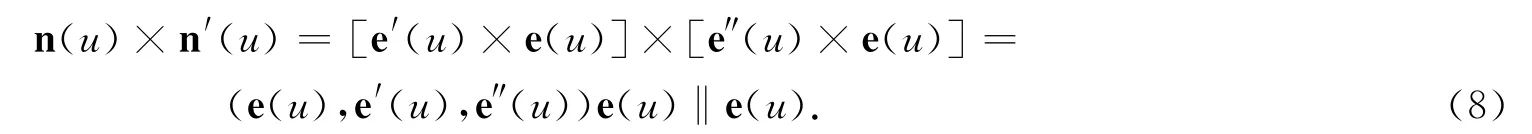
由(7)式和(8)式知,平面族πu的包络面的方程是:

这正是直纹曲面S的方程.
“⇐”.设曲面S是它的切平面族的包络面,由(2)式知,曲面S的法矢量是:

曲面S上M(u,ν)点的切平面的方程是:
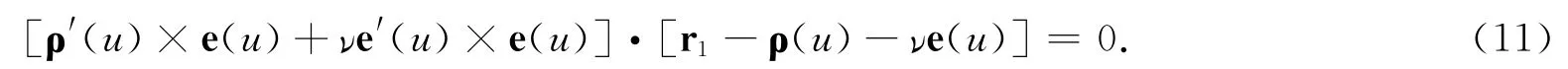
设M(u,ν)是曲面 上的任意一点,曲线C∶ν=ν(u)是经过M(u,ν)点的任意一条曲线,由(11)式得,沿曲线C,曲面S的切平面的方程是:这是单参数u的平面方程.
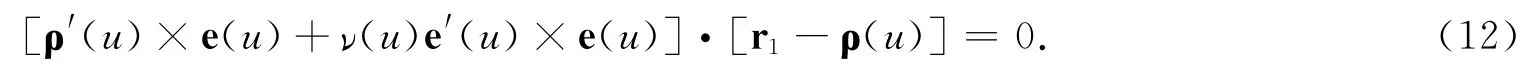
由文献[4]中定理3.6.8关于特征点的讨论知,切平面族(12)式的包络面只有以下三种情形之一:或者S是柱面,或者S是锥面,或者S是某一条曲线的切线曲面.由定理4知,直纹曲面S∶r=ρ(u)+νe(u)是可展曲面.
[1]孙国汉,赵培林,刘以均.曲面可展的条件[J].阜阳师范学院学报,1996,27(1):22~25.
[2]赵燕,纪永强.直纹曲面是可展曲面的一个充要条件[J].湖州师范学院学报,2009,31(2):26~30.
[3]吴芸,纪永强.关于曲面的高斯像的一个定理[J].湖州师范学院学报,2010,32(2):27~32.
[4]纪永强.微分几何[M].北京:高等教育出版社,2009:181~211.

