含大型风电场的电力系统调峰运行特性分析

侯婷婷 娄素华 吴耀武 张滋华 陈益民

（强电磁工程与新技术国家重点实验室（华中科技大学电气与电子工程学院） 武汉 430074）

1 引言

近年来，由于电力用户供电需求的变化，我国各电网峰谷差正在逐年增大，调峰的难度日益增大。特别是随着风力发电、太阳能发电等可再生能源发电的快速发展[1]，尤其是风力发电以其技术相对成熟、成本较低、蕴量巨大和不污染环境等优点在世界各国都得到了快速发展，大型风电场并网发电成为世界风电未来发展的趋势[2,3]，因此，这种大规模随机性、难预测性的电力并网将给系统调峰带来更大的挑战。同时，电网调峰经济运行在电力企业的生产经营中占有很重要的位置，虽然经济调峰时段只占整个电网运行总时段的 1/3，但对全网经济运行效益的影响却远远超过 1/3，对电网运行的经济性具有决定性的影响[4]。因此，研究大型风电场的调峰容量需求特性，并提出含大型风电场的电力系统调峰运行模拟分析方法具有非常重要的意义。

近几年，国内外专家学者对风电并网的相关研究工作非常重视[5-9]，对其带来的调峰问题也进行了一些初步的研究[10-12]。文献[10]结合西北电网的具体情况，提出一种采用西北水电、火电联合为风电调峰时的水电、火电调峰能力的实用计算方法；文献[11]从电网的负荷特性和电源构成着手分析2010年京津塘电网的调峰能力，进而粗略给出可接受的风电容量范围；文献[10, 11]均是结合具体电网的情况，分析风电场所在系统可提供的调峰能力，模型不具有通用性。文献[12]采用风速的 Weibull分布函数模拟的风电场时序出力曲线，基于净负荷峰谷差的变化来评价风电对系统峰谷差的影响。而事实上，风电并网系统的调峰能力和调峰运行特性，与系统负荷特性、电源特性以及风电出力特性有着密切的关系，单纯的分析风电的出力特性或者系统的调峰能力都是不全面的。目前的研究大都对风电接入系统以后给电网调峰带来的调峰压力进行较粗略的宏观分析，但是缺少对系统调峰运行特性问题进行通用的定量分析和建模。因此，对于风电出力的随机性给并网系统调峰带来的影响以及含风电场的系统调峰运行特性问题急需进一步的深入研究。

电力系统的调峰需求是指运行周期内系统的最大负荷与最小负荷的差值，因此，研究含大型风电场的电力系统的调峰问题需要结合整个运行周期内的系统负荷特性和风电场出力来分析。风电出力的随机性、间歇性以及难预测性使得风电的调峰容量需求具有很大的随机性，这是含风电的电力系统调峰问题不同于传统系统调峰分析的关键。

针对风电出力的随机性，结合系统的负荷特性，本文建立了含风电系统的调峰容量需求模型，采用典型场景描述风电接入系统后调峰容量需求的随机特性。基于调峰容量需求模型，提出了一种含大规模风电的电力系统调峰运行特性分析方法。考虑到风电调峰容量需求的随机性，在模型目标函数中计及了系统上调峰能力不足造成的缺电损失费和下调峰能力不足造成的弃风惩罚费用。最后应用本文提出的模型对一个测试系统进行了计算和分析证明本文模型的有效性和实用性。

2 含风电系统的调峰容量需求模型

含风电系统的调峰容量需求来源于风电出力的变化和负荷的峰谷差，需求的大小则与两者的时序相关性密切相关。为了获得能够用于含风电系统调峰分析的风电出力模型，本文借鉴电力系统选取典型负荷曲线的思路，通过对净负荷的峰谷差数据进行统计分析和场景削减技术，得到用于含风电系统调峰分析的典型风电出力场景及对应的概率。

2.1 含风电系统的调峰容量需求

在电力系统运行中，为充分利用可再生能源，将风电出力处理成负负荷，与原始负荷叠加后得到净负荷曲线。系统的调峰容量需求分析基于净负荷来进行，这样既兼顾了负荷的调峰需求和风电出力的变化，又考虑了两者之间的相关性。净负荷Lnet可表示为

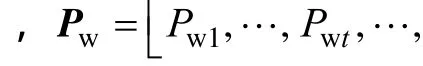
含风电系统的调峰容量需求是指运行周期T内系统最大净负荷与最小净负荷之差，即系统净负荷的峰谷差。由于风电出力的不确定性，风电出力可能有多种情况，根据式（1）得到的净负荷也具有多个场景。在一个运行周期内，对应风电出力场景i的系统调峰容量需求可表示为

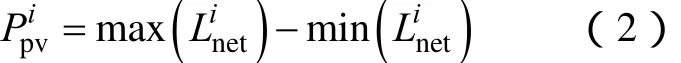
2.2 含风电系统的调峰容量需求分类

借鉴well-being分析原理[13]，依据风电场接入对系统调峰容量需求的影响可将含风电系统的调峰容量需求场景分为 Healthy、Marginal和 Risk等三种类型。其物理含义分别是，Healthy代表系统的调峰容量需求小于风电场接入系统前的调峰容量需求Lpv，即风电场的接入改善了系统的调峰状况；Risk代表系统可提供的调峰容量Cpv小于系统的调峰容量需求，即系统满足不了含风电系统的调峰容量需求；而Marginal代表除上面两种类别之外的调峰容量需求，即风电场的接入加大了系统的调峰压力，但是，系统可提供的调峰容量Cpv还可满足含风电系统的调峰容量需求。这种分类方法明确表示了风电场接入对系统的调峰容量需求影响的三种情况，并较好地区分了含风电系统的调峰压力状态。

根据上述分类方法，含风电系统调峰容量需求集合Ωpv被分成三个子集：ΩH,pv、ΩM,pv、ΩR,pv，其包括的场景及对应的概率分别如式（3）和式（4）所示。

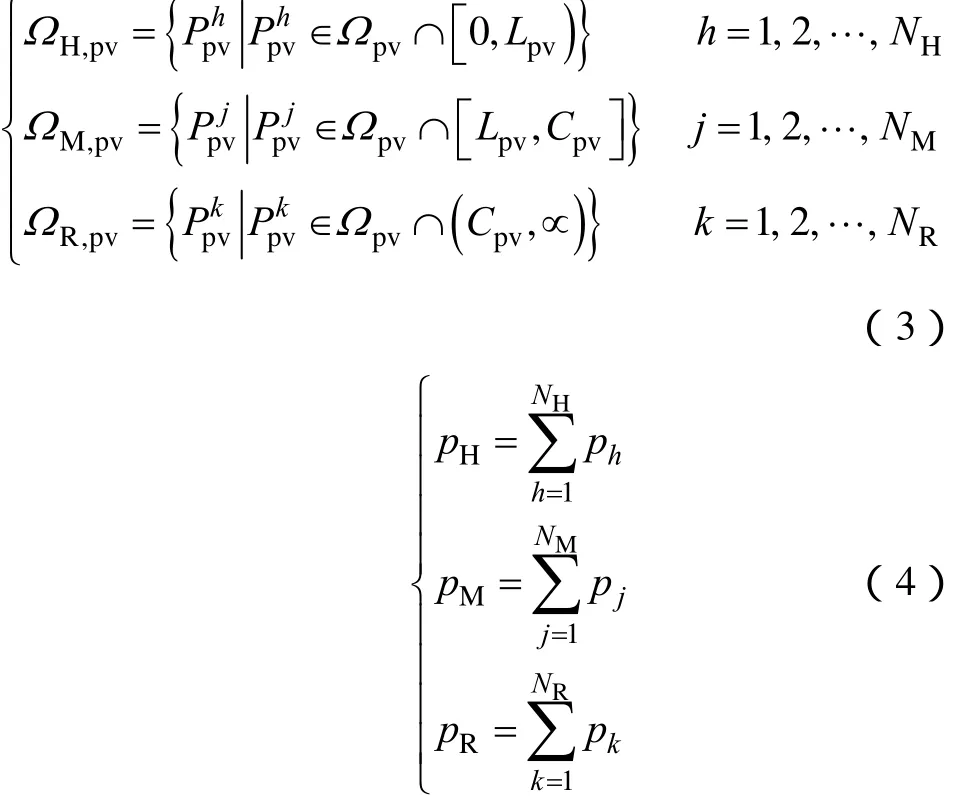
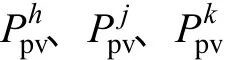
2.3 调峰容量需求场景削减

受计算复杂性的限制，实际工作中不可能对每一个场景都进行详细的分析和评估，因此，采用基于Kantorovich Distance（KD）的forward场景削减技术[14]对各调峰容量需求状态包括的场景进行削减，进而得到能够代表各调峰容量需求状态的典型风电出力场景及对应的概率。

基于 KD的 forward场景削减技术是一个优化的过程，通过反复迭代，从原始场景集合Ω中寻找与其他场景KD距离最小的场景，将其置入目标场景集合Ω′。两个场景集Ω和Ω′的KD定义如下[15]：

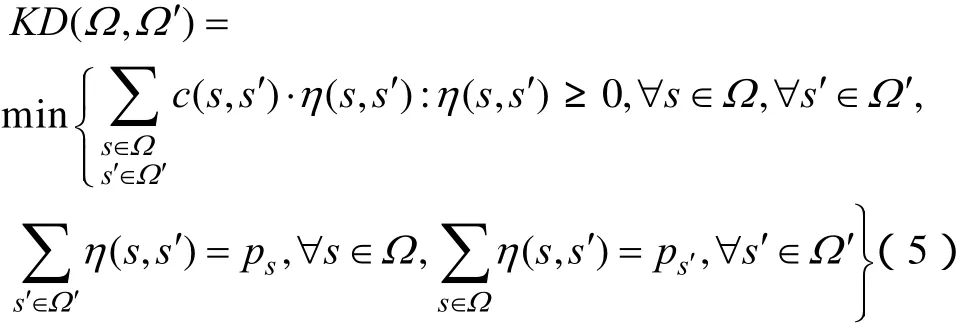
式中，c(⋅)是一个非负、连续、对称的距离函数；s和s′分别为原始场景集Ω和目标场景集Ω′中的场景；ps和ps′分别为场景s和s′在Ω和Ω′中的概率。

对于某一种调峰容量需求状态而言，Ω代表含风电系统调峰容量需求的初始场景集合，而Ω′代表削减后的目标场景集合，因此，式（5）等效为

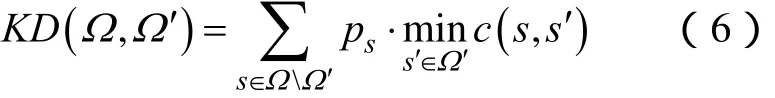
在本文中，将c(s,s′)定义为两个场景的调峰容量需求之差的绝对值，即

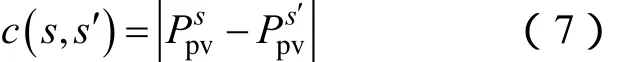
采用上面阐述的基于KD的 forward场景削减技术即可对各类调峰容量需求状态子集进行场景削减。在削减后得到的目标场景集Ω′中，每个调峰容量需求场景Pp′v对应的风电出力曲线PW′即选取的典型风电出力曲线，这些典型风电曲线能够反映随机性的风电加入后对系统调峰需求的影响。

为了在调峰需求分析中，合理评估风力发电的经济性，获得的风电典型出力曲线必须能够正确反映风能的电量特性，即与风电场的期望发电量保持一致。为此，需根据运行周期内风电场的期望发电量对目标场景集中与原始场景集KD距离最短的场景s′对应的风电出力曲线进行修正，修正公式为

对于每类调峰容量需求包括的场景进行削减的最终结果及其对应的概率如下所示：

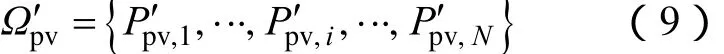
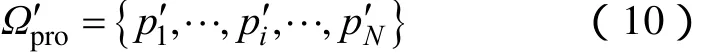
2.4 含风电系统的调峰容量需求模型

经过上面的调峰容量需求场景状态分类以及场景削减，含风电系统的调峰容量需求模型如下：

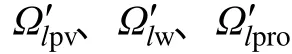
此风电调峰容量需求模型通过选取典型的系统调峰需求场景对风电调峰容量需求的随机性进行建模，从而可应用于下面的考虑风电随机性的调峰运行特性分析研究。

3 含风电场的电力系统调峰运行特性分析

3.1 目标函数

含风电场的电力系统调峰运行特性分析研究的目标是在满足系统调峰需求及各种约束条件的前提下，充分利用可再生能源，使运行周期内系统的发电成本最小。考虑到风电的随机性，在调峰平衡运行模拟模型目标函数中计及了系统由于风电变化而导致的上调峰能力不足带来的缺电损失费和下调峰能力不足带来的弃风惩罚费用。

基于第2节所建立的调峰容量需求模型，含风电系统的调峰运行特性分析模型的目标函数如下：

其中

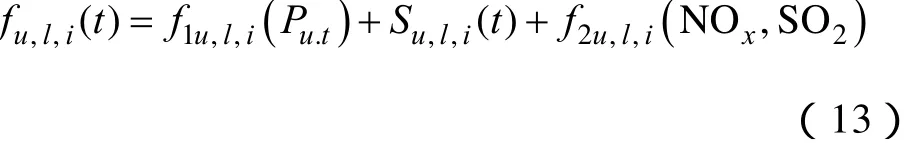
式中，F为运行周期内总费用；Nu为常规发电机组数；fu,l,i(t)为典型风电出力Plw,i对应的机组u在t时刻的发电费用，包括运行费用f1u,l,i(Pu.t)、启停费用Su,l,i(t)和 SO2及 NOx的排污费用f2u,l,i(NOx, SO2)；Ol,i(t)为系统上调峰能力不足而造成的缺电损失费；Cl,i(t)为系统下调峰能力不足造成的弃风电量惩罚费用。

Ol,i(t)和Cl,i(t)的计算式为

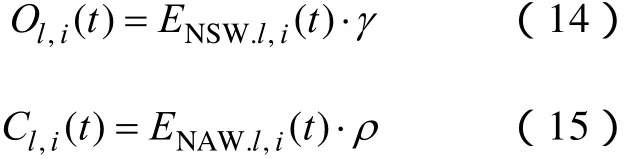
3.2 模型约束条件

含风电系统的调峰运行特性分析模型的约束条件包括系统运行约束、常规机组约束和风电场出力相关的约束。对于每个典型风电出力场景Plw′,i，均需满足以下约束：

（1）系统运行约束

①系统功率平衡约束

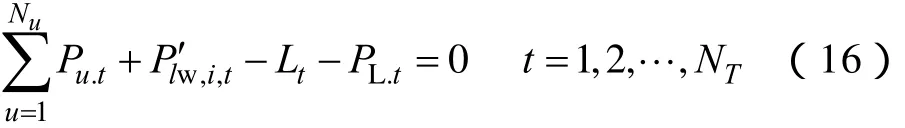
式中，Pl′w,i,t为典型风电出力Plw′,it时刻的出力；Lt、PL.t分别为时刻t系统的负荷值和网损值。

②系统备用约束

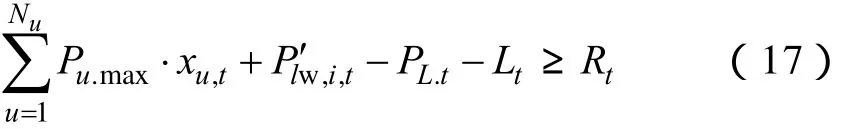
式中，Pu.max为机组u的最大出力；Rt为时刻t系统备用；xu,t为机组u的运行状态，1为开机，0为停机。

（2）常规机组约束

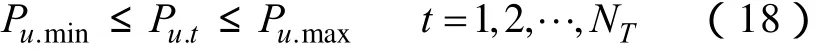
式中，Pu.min为机组u的最小技术出力。

（3）风电场运行约束

①风电场出力约束，即风电场的出力不大于风电场装机总容量：

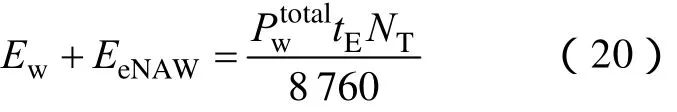
式中，Ew、EeNAW分别为系统利用的风电电量和弃风电量；tE为风电场的年期望利用小时。

4 算例分析

本文的测试系统基于某一实际系统的 2015年的负荷特性和电源数据和某一风电场的实际出力数据，采用本文提出的模型，分析电网接入风电后的调峰需求及调峰运行特性指标。系统的火电发电机组参数、不同负荷率的煤耗特性和负荷特性分别见表 1、表 2和表 3所示。最大负荷为 87 000MW，风电场总容量为17 400MW，最大负荷的20%。

表1 常规机组数据Tab.1 Conventional generator’s data

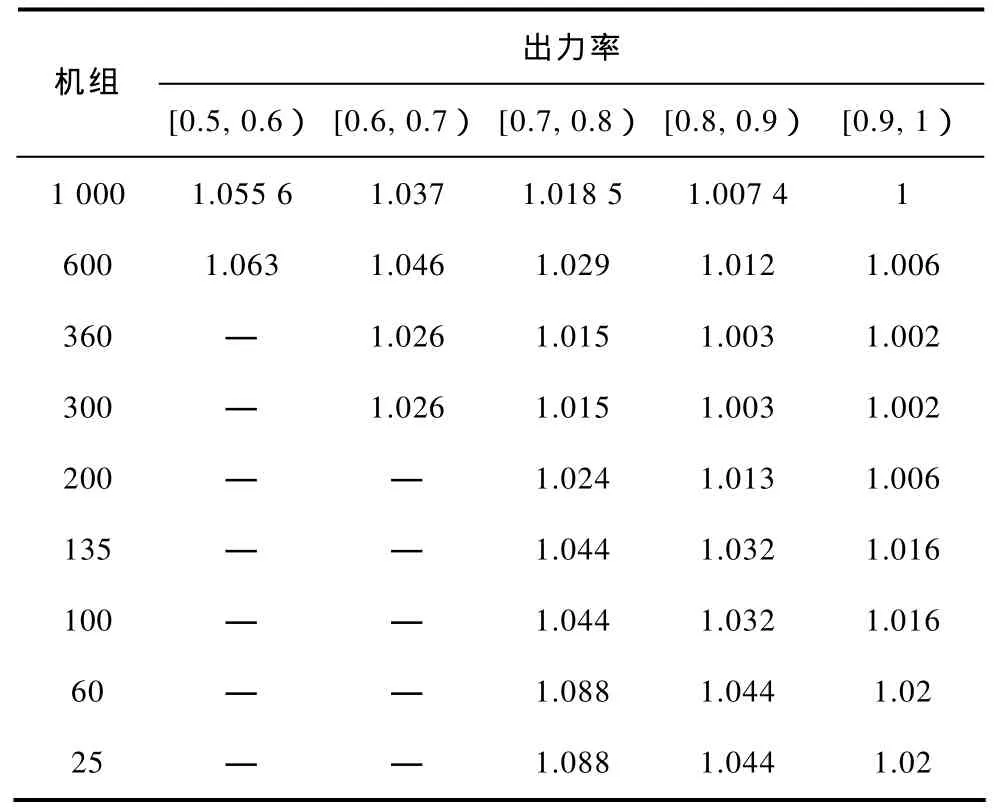
表2 常规机组煤耗特性Tab.2 Conventional generator’s characteristic of coal consumption

表3 负荷数据Tab.3 Load data

4.1 调峰需求典型场景的风电出力曲线

采用建立的含风电系统的调峰容量需求模型，对一风场接入系统后的净负荷进行建模，调峰需求目标场景集包括3个典型场景，可得出3种调峰需求状态对应的典型风电出力曲线，如下图所示。

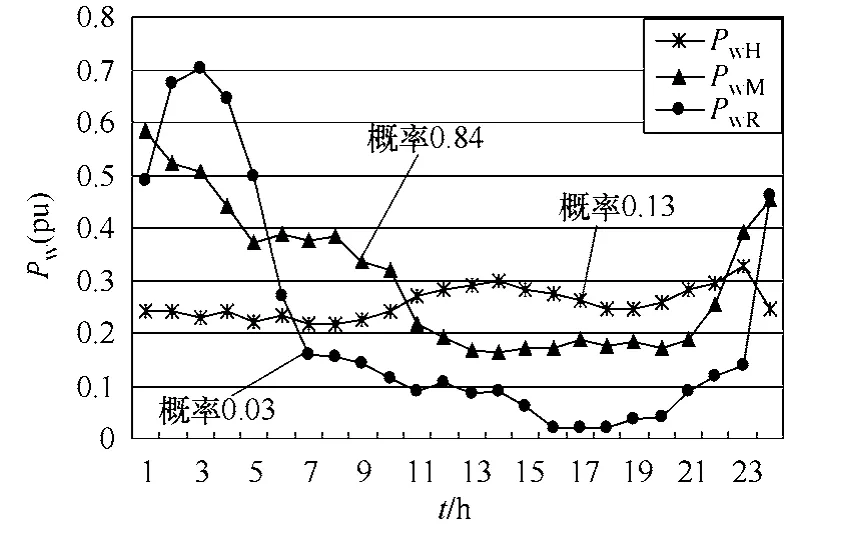
图 调峰容量需求典型场景的风电出力曲线Fig. The modeling result of wind power output curve for the selected scenarios

由图可见，采用风电调峰容量需求模型产生的3条典型风电出力曲线各不相同，反映出了风电出力的三种调峰容量需求，并且，风电接入以后，系统的调峰状态较多的集中于Marginal状态，其概率达到0.84，而Healthy和Risk状态的概率分别为0.13和0.03。由此，整体来看系统接纳此容量的风电调峰没有问题。

4.2 调峰运行特性分析

在风电调峰需求典型出力曲线基础上，进行系统的调峰运行特性分析，其运行指标见表4。

根据表4的调峰运行模拟结果可以看出，风电接入以后，系统的总燃料消耗、总排放量相对于风电接入系统以前均有所减少，火电发电量降低；同时，由于风电的波动性，风电并网系统的常规机组调峰压力增加，从而导致火电单位发电量的燃料消耗相对于风电接入前有所增加。这说明，风电的接入使并网系统的燃料消耗成本降低，但由于其波动性的影响，加大了常规机组的调峰压力，从而附加一部分调峰成本。

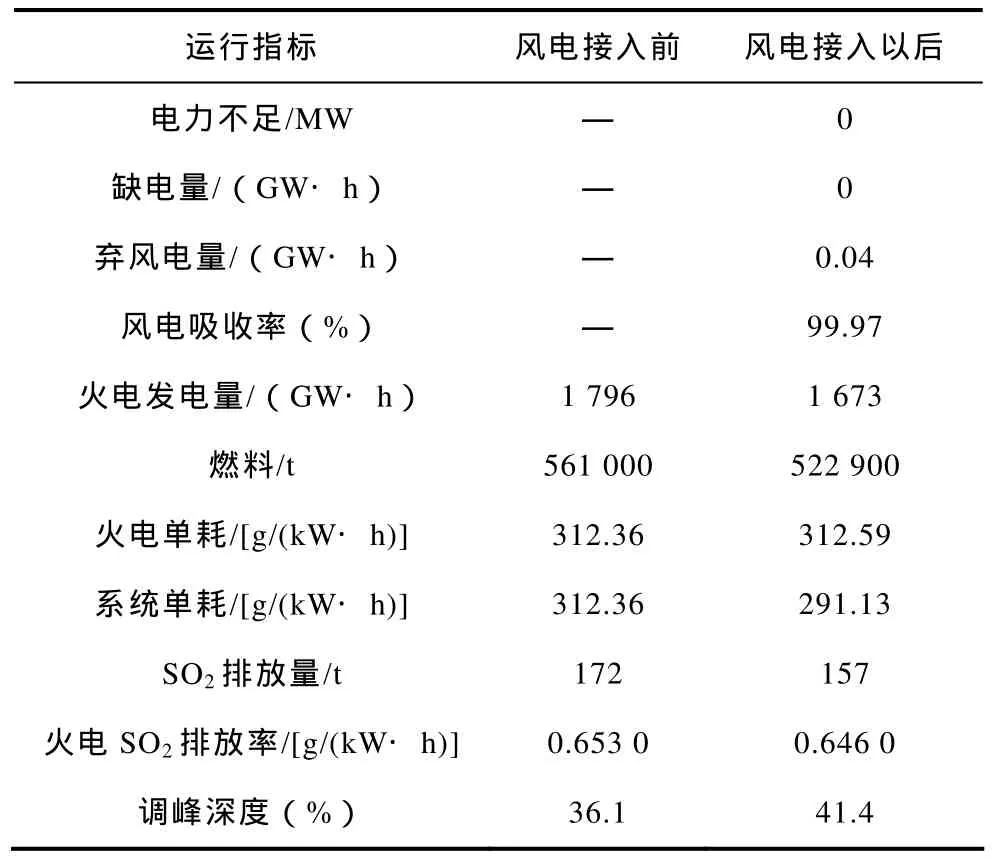
表4 调峰运行特性指标Tab.4 Indices of peak load regulation operation

4.3 风电吸纳能力分析

采用文中模型对不同渗透率风电并网系统做了调峰平衡运行模拟，风电的渗透率（风电容量占系统最大负荷的比例）以10%为步长依次增加到80%，其结果见表5。

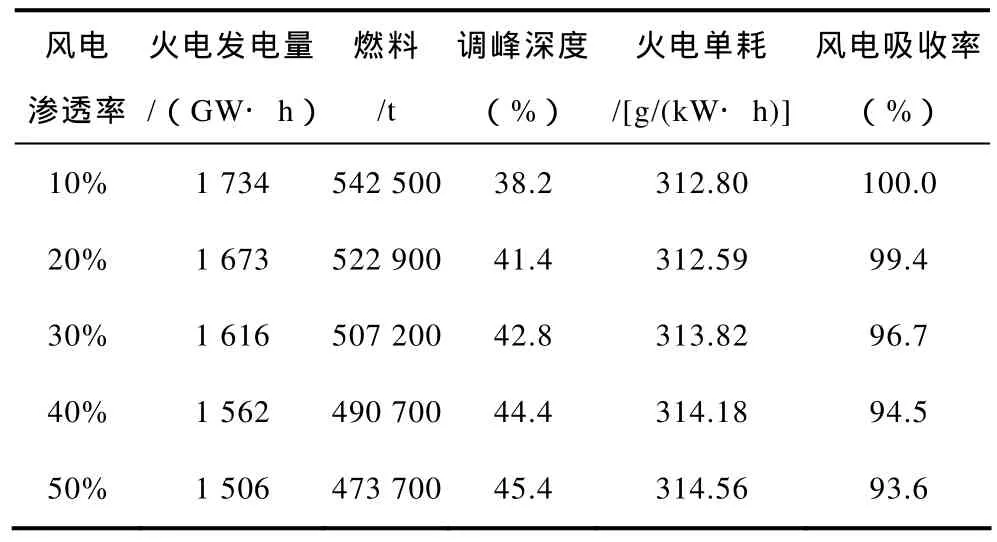
表5 不同风电并网容量时的调峰运行特性结果Tab.5 Results of peak load regulation operation characteristics for different wind power penetration

由表5可知，随着风电装机容量的增大，火电发电量和系统总煤耗量都逐步减少，这说明，增加风电接入系统的容量，在可以替代火电发电量从而节省了燃料消耗，但随着风电装机容量的增大，增加相同的风电装机替代的火电发电量越来越少。从风电渗透率30%开始，随着风电装机容量的增大，火电单位发电量的煤耗呈增加的趋势，这是因为，随着风电容量的增加，火电的调峰深度逐步加大，火电机组的出力率降低，从而导致火电单位煤耗的增大。

4.4 模型准确性验证

采用枚举法对所有的风电出力场景进行了调峰平衡运行模拟，与文中所提模型的结果比较见表6。

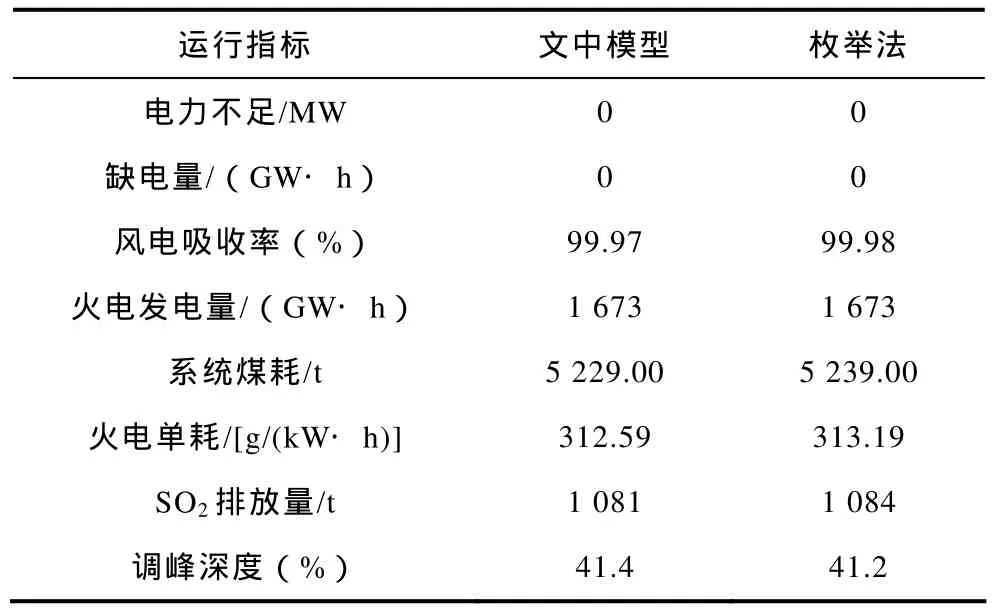
表6 两种方法的结果对比Tab.6 Comparison of results of two different methods

由表6的结果对比可以看出，系统的各类运行指标的偏差均比较小，偏差在0.5%以内，最大的为火电调峰深度，偏差为 0.48%，火电发电量、系统煤耗、SO2排放量的偏差绝对值分别为0、0.19%、0.34%；总的系统吸纳的风电发电量偏差为0.01%。

总之，从系统各类运行指标来看，采用本文提出的含风电系统的调峰容量需求模型和方法，选取3个典型调峰需求场景对应的风电出力曲线进行调峰运行特性分析，其计算结果偏差均在0.5%以内，若提高典型场景的数目，其计算结果的偏差会进一步减小，在具体的实际工作中，可依据工作具体的性质及精度要求而定。

5 结论

风电出力的随机性和难预测性给含大容量风电的电力系统调峰运行分析带来了巨大的挑战。本文针对风电出力特性建立了含风电系统的调峰容量需求模型，借助KD场景削减技术选取出典型的系统调峰需求场景。基于建立的含风电调峰容量需求模型，提出了一种含风电电力系统的调峰运行特性分析方法。通过对典型算例系统的调峰平衡运行模拟及分析可以看出，本文提出的含风电系统调峰运行特性分析方法，其计算结果精度较高，且大大降低了计算的复杂性，有利于系统规划人员从整体上直观、清晰地分析风电对系统调峰压力及运行特性的影响，便于应用于工程实际。

[1] Valenzuela Jorge, Wang Jianhui. A probabilistic model for assessing the long-term economics of wind energy[J]. Electric Power Systems Research, 2011,81(4): 853-861.

[2] 张丽英, 叶廷路, 辛耀中, 等. 大规模风电接入电网的相关问题及措施[J]. 中国电机工程学报, 2010,30(25): 1-9.Zhang Liying, Ye Tinglu, Xin Yaozhong, et al.Problems and measures of power grid accommodating large scale wind power[J]. Proceedings of the CSEE,2010, 30(25): 1-9.

[3] 肖创英, 汪宁渤, 丁坤, 等. 甘肃酒泉风电功率调节方式的研究[J]. 中国电机工程学报, 2010, 30(10): 1-7.Xiao Chuangying, Wang Ningbo, Ding Kun, et al.System power regulation scheme for Jiuquan wind power base[J]. Proceedings of the CSEE, 2010,30(10): 1-7.

[4] 李自明, 阳薇, 张扬军, 等. 电网经济调峰研究的探讨[J]. 黑龙江电力, 2001, 23(5): 315-318.Li Ziming, Yang Wei, Zhang Yangjun, et al.Economic peak avoidance on electric power supply network[J]. Heilongjiang Electric Power, 2001, 23(5):315-318.

[5] Driesen J, Belmans R. Distributed generation:challenges and possible solutions[C]. 2006 IEEE Power Engineering Society General Meeting,Montreal, Canada, 2006.

[6] H Bludszuweit, J A Domínguez-Navarro, A Llombart.Statistical analysis of wind power forecast error[J].IEEE Transactions on Power Systems, 2008, 23(3):983-991.

[7] 栗文义, 张保会, 巴根. 风能大规模利用对电力系统可靠性的影响[J]. 中国电机工程学报, 2008,28(1): 100-105.Li Wenyi, Zhang Baohui, Ba Gen. Reliability impacts of large scale utilization of wind energy on electric power systems[J]. Proceedings of the CSEE, 2008, 28(1): 100-105.

[8] 张节潭, 程浩忠, 胡泽春, 等. 含风电场的电力系统随机生产模拟[J]. 中国电机工程学报, 2009,29(28): 34-39.Zhang Jietan, Cheng Haozhong, Hu Zechun, et al.Power system probabilistic production simulation including wind farms[J]. Proceedings of the CSEE,2009, 29(28): 34-39.

[9] 周玮, 彭昱, 孙辉, 等. 含风电场的电力系统动态经济调度[J]. 中国电机工程学报, 2009, 29(25):13-18.Zhou Wei, Peng Yu, Sun Hui, et al. Dynamic economic dispatch in wind power integrated system[J].Proceedings of the CSEE, 2009, 29(25): 13-18.

[10] 衣立东, 朱敏奕, 魏磊, 等. 风电并网后西北电网调峰能力的计算方法[J]. 电网技术, 2010, 34(2):129-132.Yi Lidong, Zhu Minyi, Wei Lei, et al. A computing method for peak load regulation ability of Northwest China power grid connected with large-scale wind farms[J]. Power System Technology, 2010, 34(2):129-132.

[11] 李付强, 王彬, 涂少良, 等. 京津唐电网风力发电并网调峰特性分析[J]. 电网技术, 2009, 33(18):128-132.Li Fuqiang, Wang Bin, Tu Shaoliang, et al. Analysis on peak load regulation performance of Beijing-Tianjin-Tangshan Power Grid with wind farms connected[J]. Power System Technology, 2009, 33(18): 129-132.

[12] 张宁, 周天睿, 段长刚, 等. 大规模风电场接入对电力系统调峰的影响[J]. 电网技术, 2010, 34(1):152-159.Zhang Ning, Zhou Tianrui, Duan Changgang, et al.Impact of large-scale wind farm connecting with power grid on peak load regulation demand[J]. Power System Technology, 2010, 34(1): 152-159.

[13] Dange Huang, Billionton R. Effects of wind power on bulk system adequancy evaluation using the well-being analysis framework[J]. IEEE Transactions on Power Systems, 2009, 24(3): 1232-1240.

[14] Morales J M, Pineda S, Conejo A J, et al. A scenario reduction for futures market trading in electricity markets[J]. IEEE Transactions on Power Systems,2009, 24(2): 878-888.

[15] Rachev S T. Probability metrics and the stability of stochastic models[M]. Chichester, U. K.: Wiley, 1991.