基于R i f e-V i n c e n t窗的录波电流谐波分析方法

曹敏，熊浩，刘然，张淮清

（1.云南电力试验研究院，云南昆明 650217；2.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

随着电力系统中高电压大容量冲击性负荷以及电力电子装置等非线性设备的增加，电网的谐波污染日益严重并危害系统运行的稳定性和安全性[1-2]。传统的FFT算法在进行谐波分析时，由于截断误差和非整周期采样，不可避免地会产生较大的频谱泄漏和栅栏效应，导致FFT的结果在频率、幅值、相位上都存在偏差，严重影响谐波计算精度。

加窗插值是一种将被测信号与窗函数的乘积作FFT运算，并对结果进行修正的方法。加窗可有效抑制频谱泄漏，减小频谱间的干扰；插值可以减少栅栏效应的影响，从而改善FFT算法的谐波分析精度[3-5]。本文选取了Hanning窗和5项Rife_Vincent窗（简称R_V窗），对它们的频谱曲线主瓣宽度、旁瓣峰值电平以及旁瓣衰减速度等主要参数进行比较，定性分析了在谐波计算中的优劣，推导了相应的高阶偏差修正公式及简化形式；并应用2种窗函数对仿真和实测数据进行了分析，以验证和考察了二者的谐波分析效果。

1 加窗插值的基本原理

设电网信号采样序列为：

式中，Ts=1-fs为采样周期；ωm=2πfm；M为最高谐波次数；Am、fm、θm分别为各次谐波的幅值、频率和初相角。x（n）的离散时间傅里叶变换（DTFT）为：

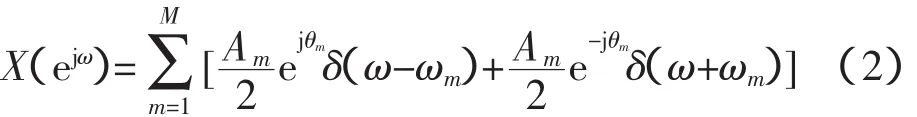
用同长度的窗函数w（n）对信号x（n）加以截断，就可以得到一个加窗函数序列：

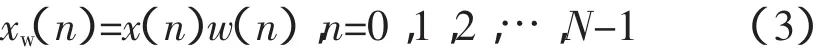
设窗函数的DTFT为W（ejω）=W（ω）e-jω，则加窗序列xw（n）的DTFT为：

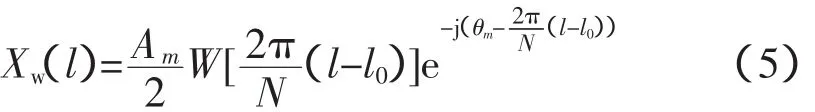
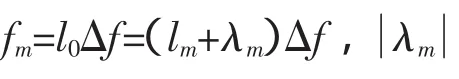
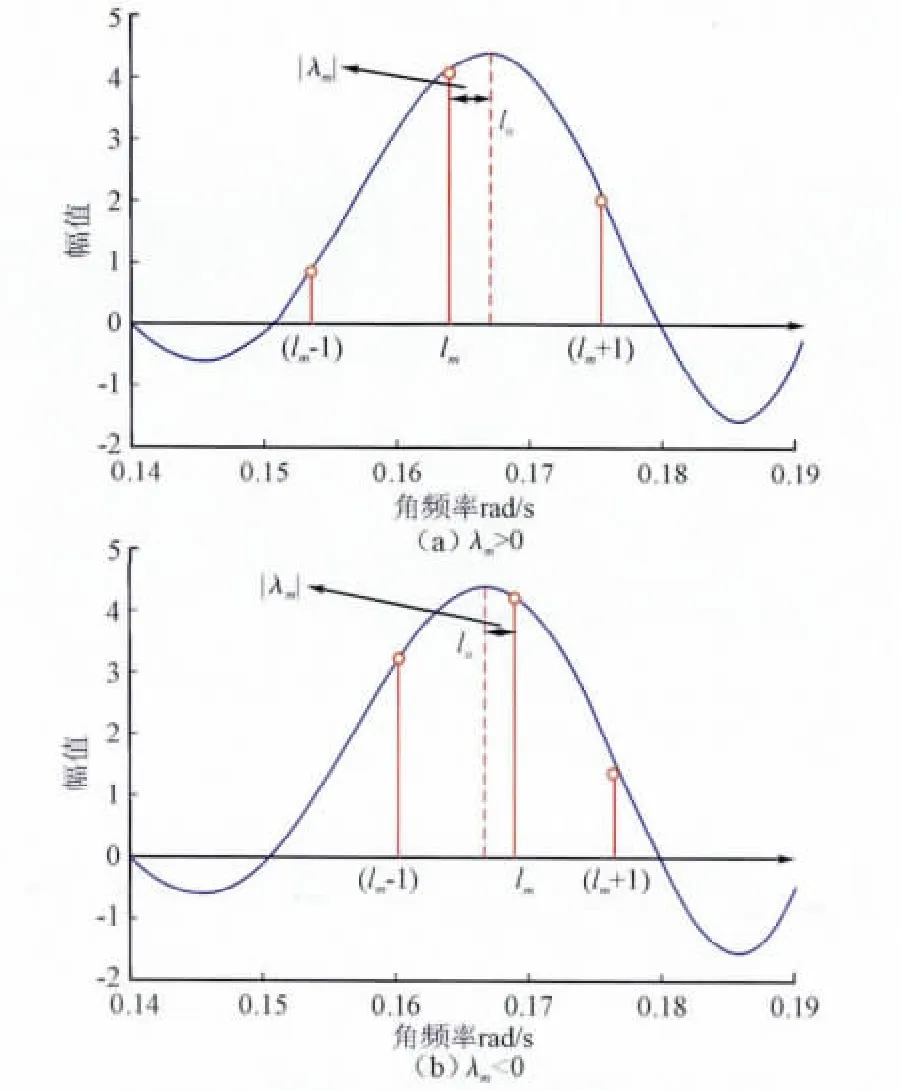
图1 非同步采样的信号离散频谱Fig.1 The discrete spectrum of the signal by asynchronous

令最大与次大谱线的幅值之比为α，即：

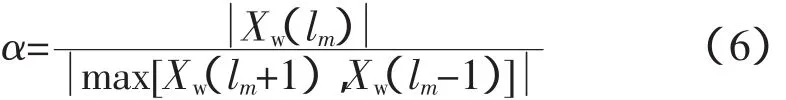
带入式（5）得：

因而，计算中根据找到的各次谐波最大和次大谱线，可计算α并推出偏差λm的值，从而得到各次谐波频率、幅值和相角的修正公式如下：

2 Hanning与R_V窗的比较及其修正公式

2.1 2种窗函数的比较

Hanning窗和R_V窗都是升余弦函数窗，而余弦函数与信号卷积时可使除主要谱线外的其他谱线相互抵消，因而能改善频谱泄漏、减少截断误差。窗函数的性能主要通过主瓣宽度、旁瓣峰值电平和旁瓣衰减速率反映。在加窗插值FFF中，要求窗函数的主瓣窄以提高频率分辨能力；要求旁瓣峰值电平小和衰减速率快，进而减少频率泄漏和各次谐波间影响[6]。图2~3给出了Hanning窗和R_V窗时频域曲线，可见：虽然R_V窗主瓣比Hanning窗宽，但旁瓣衰减达到了-73.6 dB，远低于Hanning窗的-32 dB，且旁瓣衰减速率高达30 dB/oct，高于Hanning窗的18 dB/oct。从定性来看，R_V窗频率泄漏要少于Hanning窗，谐波分析精度要高于Hanning窗。

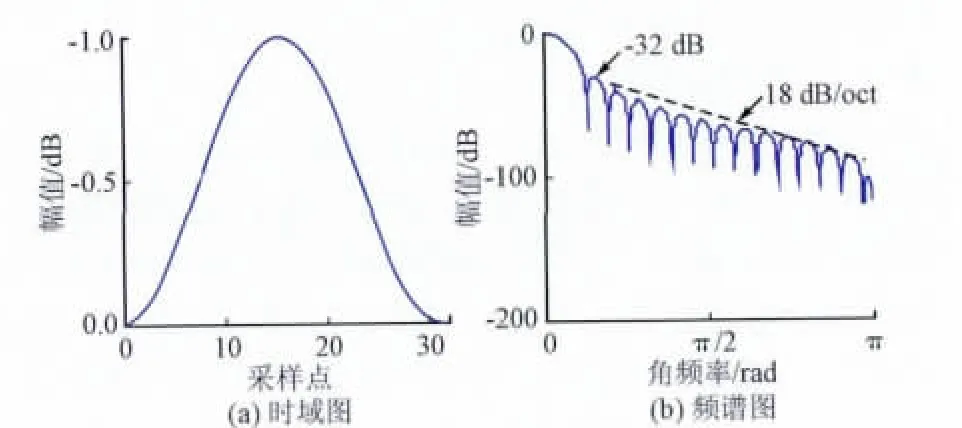
图2 Hanning窗及其频谱Fig.2 The time domain and spectrum of Hanning window

图3 R_V窗及其频谱Fig.3 The time domain and spectrum of R_V window

2.2 Hanning与R_V窗的修正公式

1）Hanning窗。函数表达式为：

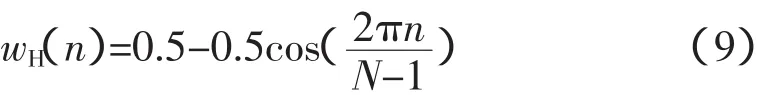
离散傅里叶变换为：

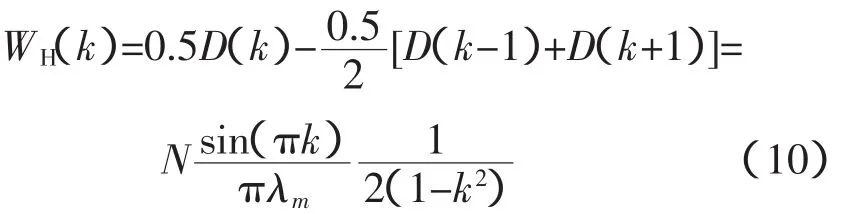
将λm带入WH（k）得：

离散傅里叶变换结果为：

将λm带入WR（k）得：

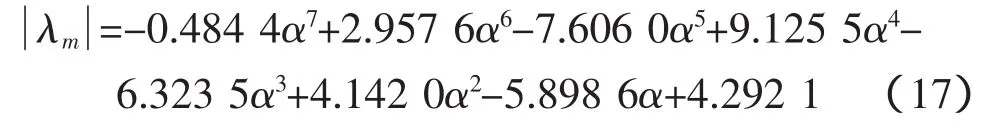
3 仿真计算及实例分析

3.1 仿真计算

为验证加窗插值FFT算法的准确性以及R_V窗和Hanning窗性能，选取以下信号作谐波仿真：

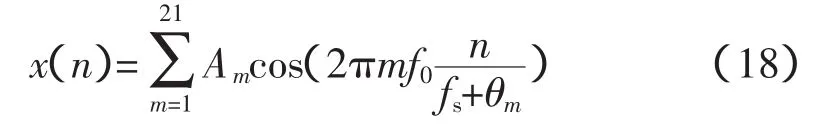
其基波频率f0=49.5Hz，基波及各次谐波参数见表1。

表1 基波及谐波参数Tab.1 Parameters of harmonic signal

仿真中，取采样频率fs=5000 Hz，窗函数点数N=1024。仿真计算的参数见表2~4。

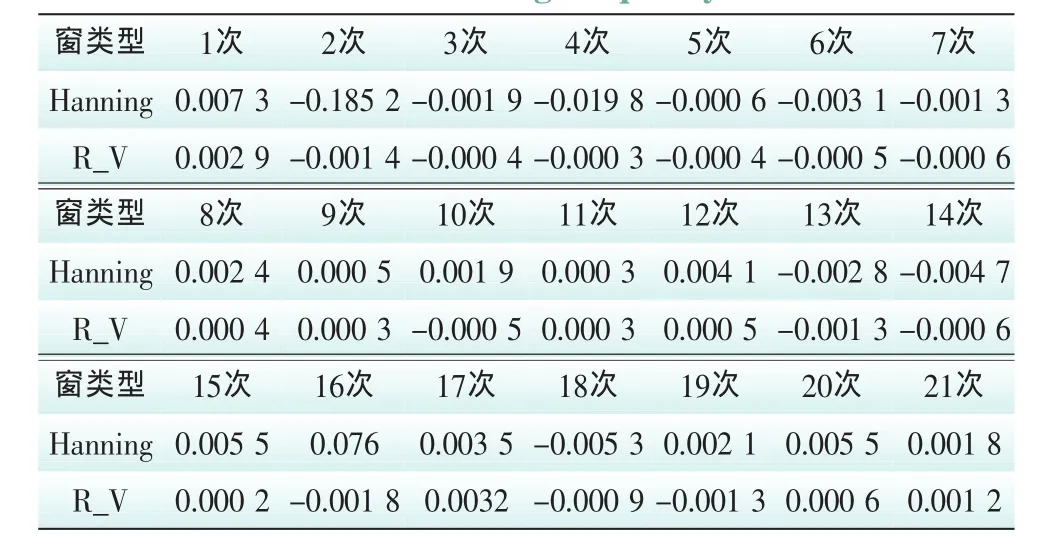
表2 频率计算误差比较Tab.2 Comparison of relative errors in calculating frequency %

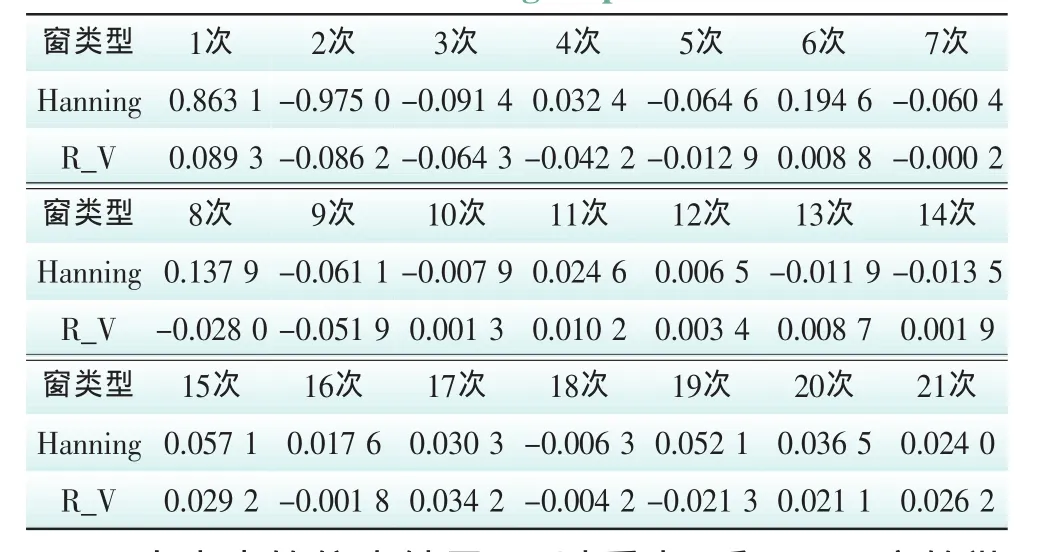
表3 幅值计算误差比较Tab.3 Comparison of relative errors in calculating amplitude %

由表中的仿真结果，可以看出：采用R_V窗的谐波计算精度整体优于Hanning窗，特别在幅值较小的偶次谐波处R_V窗的精度约高出1~2个数量级。其频率计算相对误差绝对值低于0.003%，幅值计算相对误差绝对值低于0.09%，相角计算相对误差绝对值低于1.1%。

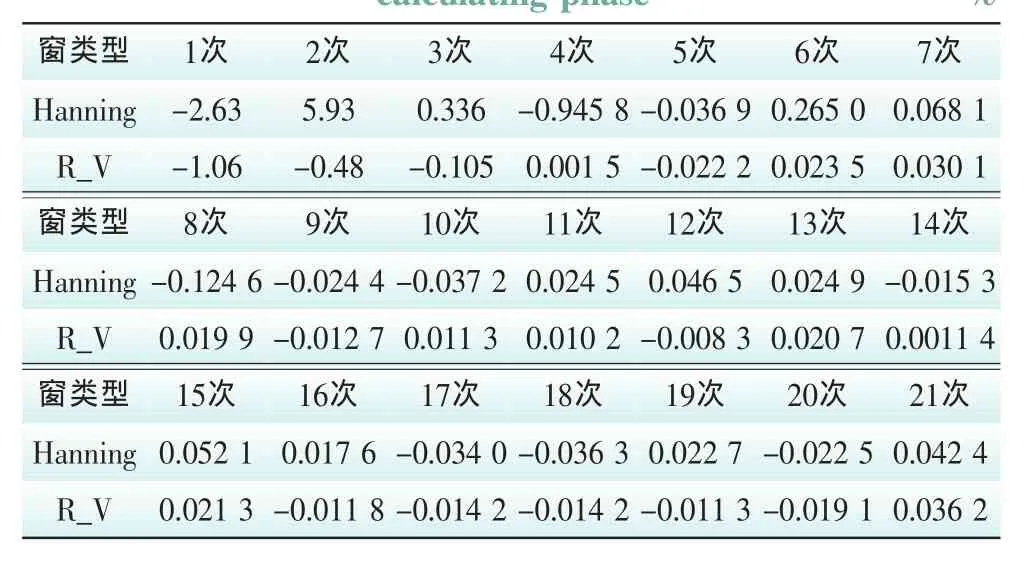
表4 相角相对误差比较Tab.4 Comparison of relative errors in calculating phase %

此外，还可从时域角度分析2种窗函数的谐波分析性能，即利用仿真信号和基于谐波计算的参数信号模型在采样时刻点的误差。其思路为：根据谐波分析给出了频率、幅值和相位的近似值f軇m、A軒m和θ軌m得到信号的近似模型：

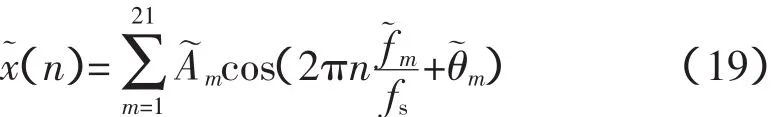
然后，计算近似模型和原信号在采样点处的相对均方误差Err_RMS，其定义如下：

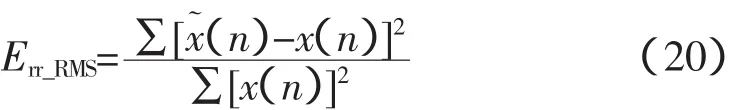
本例中，Hanning窗计算的相对均方误差为2.51×10-4%；R_V窗为1.22×10-4%，表明从时域来看R_V窗谐波分析精度依然强于Hanning窗。

3.2 实例计算

最后，利用基于R_V窗的加窗插值FFT算法对某电力局的电流数据进行谐波分析，基波频率为49.8Hz，各次谐波估算参数见表5。

求得估算信号的解析解并离散化，计算出实际信号对应点的相对误差Err_RMS=0.0015%。最后，作出估算信号x軇（n）与实际信号x（n）的曲线如图4。可以看出，两者是非常接近的。

4 结论

1）相对于Hanning窗插值，R_V窗旁瓣性能更优，频谱泄漏更小，所以其谐波参数的估算精度较Hanning窗有了较大的提升。

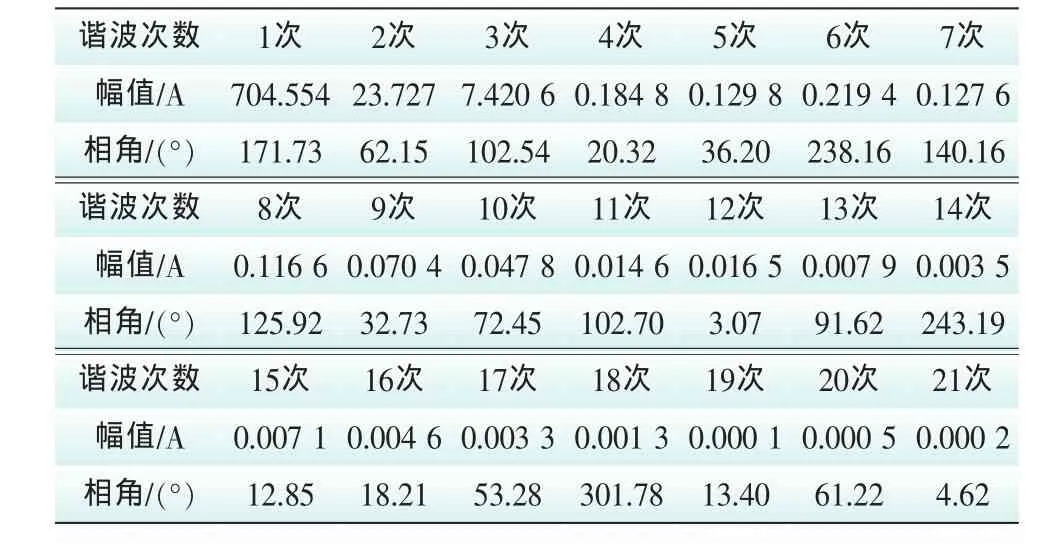
表5 实际信号基波及谐波参数Tab.5 Parameters of estimated harmonic signal

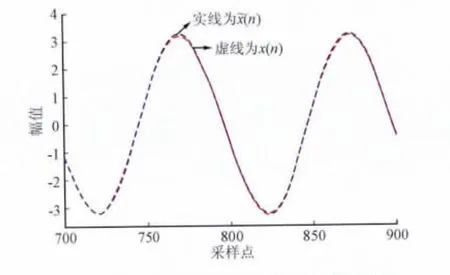
图4 估算信号x軌（n）与实际信号x（n）的对比Fig.4 Comparison of estimated signal x軌（n）and actual signal x（n）

2）从时域角度来描述实测数据的谐波分析误差是可行而有效的。

3）基于R_V窗的加窗插值方法对实际电网运行数据的谐波分析有较好精度。

[1] 周俊，王小海，祁才君．基于Blackman窗函数的插值FFT在电网谐波信号分析中的应用[J]．浙江大学学报：理学版，2006，33（6）:650-653．ZHOU Jun，WANG Xiao-hai，QI Cai-jun．Estimation of electrical harmonic parameters by using the interpolated FFT algorithm based on Blackman window[J]．Journal of Zhejiang University：Science Edition，2006，33（6）：650-653（in Chinese）．

[2]黄峰，杨洪耕.基于快速傅里叶变换的谐波和间谐波检测修正算法[J].电网与清洁能源，2010，26（6）:28-32.HUANG Feng,YANG Hong-geng.A modified algorithm based on fast Fourier transform for harmonics and interharmonics detection[J].Power System and Clean Energy，2010，26（6）:28-32（in Chinese）.

[3] 杨冠鲁，姚若苹，余尤好．采用加窗插值FFT与逐幅谐波消去法的电机谐波算法[J]．福州大学学报：自然科学版，2006，34（3）：352-356．YANG Guan-lu，YAO Ruo-ping，YU You-hao．Harmonic analysis in the electric machine based on windows and interpolated FFT and harmonic expurgation according to amplitude[J]．Journal fo Fuzhou University：Natural Science Edition ，2006，34（3）：352-356（in Chinese）.

[4] 庞浩，李东霞，俎云霄，等．应用FFT进行电力系统谐波分析的改进算法[J]．中国电机工程学报，2003，23（6）：50-54.PANG Hao，LI Dong-xia，ZU Yun-xiao，et a1．An improved algorithm for harmonic analysis of power system using FFT Technique[J]．Proceedings of the CSEE，2003，23（6）：50-54（in Chinese）．

[5] 肖先勇，王楠，刘亚梅.基于多项式逼近的单峰谱线插值算法在间谐波分析中的应用[J].电网技术，2008，32（18）:57-61.XIAO Xian-yong，WANG Nan，LIU Ya-mei.Application ofpolynomialapproximation based single peak spectral lines interpolation algorithm in interharmonic analysis[J].Power SystemTechnology，2008，32（18）:57-60（in Chinese）．

[6] 曾博，滕召胜，温和，等.莱夫-文森特窗插值FFT谐波分析方法[J].中国电机工程学报，2009，29（10）:115-120.ZENG Bo，TENG Zhao-sheng， WEN He， et al.An approach for harmonic analysis based on rife-vincent window interpolation FFT[J].Proceedings of the CSEE，2009，29（10）:115-120（in Chinese）.