影响H H T方法辨识低频振荡模式参数精度的技术分析与改进
易建波,黄琦,丁理杰
(1.电子科技大学电力系统广域测量与控制四川省重点实验室,四川成都 611731;2.四川省电力科学研究院,四川成都 610072)
低频振荡是现代电力系统中发生频繁、对系统稳定运行造成严重影响的一类事故,已成为威胁互联电网安全稳定运行,制约电网传输能力的重要因素之一[1-2]。目前研究电力系统低频振荡问题的方法主要可分为2种。第一种是以电力系统结构模型为基础,通过模型参数建立微分方程,根据李亚普诺夫稳定性第一定理分析系统的稳定性,主要以特征根QR法为代表[3]。但该方法受制于模型的阶数、参数不精确性、未建模动态和交互模态的影响,增加了应用的难度,分析结果的准确性受到很大影响。第二种方法是采用现代信号处理方法分析低频振荡信号特征,主要以FFT算法、小波分析法、Prony算法为代表。但由于电力系统自身的高维、强非线性等特点以及各种信号处理方法的适应环境不尽相同,因此各种方法都存在一些缺点。FFT算法通过频谱分析可得到信号频率,但其无法分析信号的阻尼特性;小波分析难以解决频率交叠和自适应小波基问题;Prony算法和ARMA算法受噪声、系统实际阶数的影响较大,参数辨识的精度难以保证[4-5]。
近年来,电力系统广域测量系统(WAMS)在世界各国电网得到广泛应用,使得电力系统运行过程中的各状态量能够都得到实时监测,从而引起基于实测信号的数据分析方法的研究高潮[5]。由于电力系统低频振荡信号是典型的非线性、非平稳信号,基于数据驱动HHT方法[6-7]被引入振荡信号分析领域[8-11]。随着G.Rilling等人对HHT方法中的经验模态分解算法(EMD)[12-13]不断完善,增加了该方法应用的可行性,同时国内学者不断研究HHT方法的改进方案,拓展了该方法的应用范围,同时提升了该方法的实用性[14-16]。然而,该方法缺乏坚实的理论基础,其中经验模态法分解低频振荡信号,存在如端点延拓误差、包络插值失真、模态混叠分辨率限制、过筛阻尼损失等诸多问题,严重影响了该算法的可信度和精度。
本文研究HHT方法在辨识低频振荡模式参数时存在的技术问题,提出几项技术改进方案。第一,引入极值点ARMA短期延拓方法,通过与镜像延拓混合应用,提高端点延拓精确性。第二,包络插值采用B样条插值法替代传统的三次样条插值,减小插值过冲和欠冲机率,抑制频率漂移现象。第三,定义筛分能量控制因子,有效控制IMF分量筛分过程,减小过筛引起的阻尼损失。第四,对于可能出现的混叠模态,通过Morlet小波多分辨算法构建窄带滤波器,提高算法的频率分辨率。本文的改进技术方法经过EPRI-36仿真算例实际测试,达到了较好的分析精度和应用效果。
1 基本理论
HHT方法是由数据驱动的非线性非平稳数据处理方法,首先利用经验模态分解(EMD)将信号分解为若干个固有模态函数(IMF)分量之和,然后对每个IMF分量进行Hilbert变换,得到瞬时频率和瞬时幅值。如果每个IMF分量可认定为单一模态分量,则该分量与相应的低频振荡模态对应,经过Hilbert谱分析与模态参数模型相结合的辨识方法,得到振荡模态参数的特征信息。
1.1EMD 过程
EMD方法认为,任何复杂的非线性、非平稳信号都能够分解成一组数目有限的IMF分量和一个残余分量。从本质上说,EMD是对信号进行平稳化处理的过程,可以将任意信号中不同尺度的波形或趋势逐级分解出来,产生一系列具有不同特征尺度的IMF数据序列。
IMF被定义为满足以下2个条件的函数:1)在整个信号范围内,其极值点数目和过零点数目必须相等或至多相差一个;2)对信号上的任意一点,由信号的局部极大值点定义的上包络线和信号的局部极小值点定义的下包络线的平均值为零,即上包络线和下包络线相对于时间轴局部对称。
该方法分解信号x(t)的基本步骤如下:
①提取原始信号x(t)的所有极大值点和极小值点。
②利用三次样条插值拟合x(t)极值点的上包络和下包络,并求取均值包络m1。
③ 用信号x(t)减去均值包络m1,得到新的信号h1,判断h1是否满足IMF条件。
④如果h1不满足判断条件,则以h1为原信号重复筛分;如果h1满足判断条件,则提取出一个IMF分量,剩余信号继续筛分过程,直至提取出全部IMF分量和一个无法继续筛分的残余分量rn。

式中,ci表示第i个IMF分量;rn表示残余分量。EMD方法是以一种筛分的方法提取IMF分量,从信号时频分析的角度看,类似于滤波器组,其分解得到的IMF分量是形式上关于轴对称的平稳化波形信号,并不能表达真实的物理意义。
1.2 谱分析及参数辨识
确定IMF分量与低频振荡模式之间的对应关系。首先通过Hilbert变换,对EMD分解后的每个IMF分量ci(t)(i=1,2,…,n)分别作Hilbert变换:
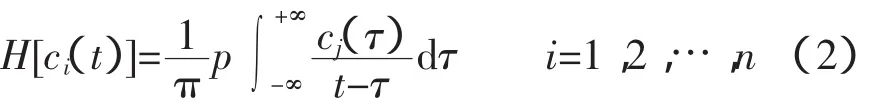
式中,p为柯西主值。原分析信号的IMF分量可以构成解析信号zi(t)
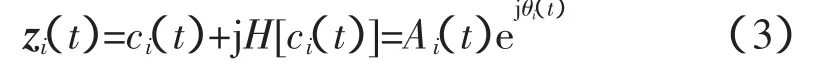
得到IMF分量ci(t)的瞬时幅值函数以及瞬时相位函数为:
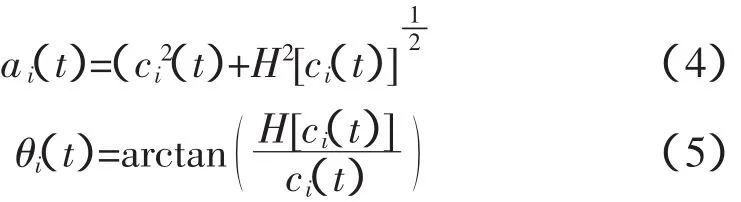
对于EMD分解得到的每个IMF分量ci(t),如果不存在模态混叠,可看作为一个单一模态信号。而是否存在模态混叠,主要判断依据是IMF分量瞬时频率谱线的特性。如果不计及瞬时频谱两端的端点效应影响,谱线随时间走势平坦,则可以认为IMF分量为一个单一振荡模态,使得IMF分量具备物理意义,同时结合低频振荡信号合成表达式,可以定义IMF分量和振荡模态之间的关系如:
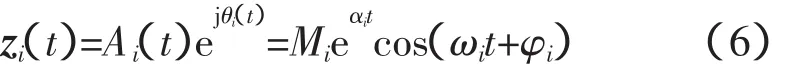
通过瞬时相位公式,可以定义ci(t)的瞬时角频率:

与之相对应的瞬时频率为:

对于低频振荡衰减因子α和振幅参数M的辨识,依靠HHT边际谱或者FFT频谱都不能直接得到。以上2种谱线都是反映振幅累积效应的,对于存在阻尼的振幅,很难直接获取。本文采用对单个IMF分量的瞬时幅值函数进行分析,求取其对数曲线,采用最小二乘法拟合求取参数αi和Mi。
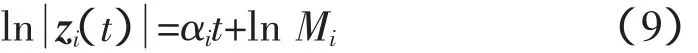
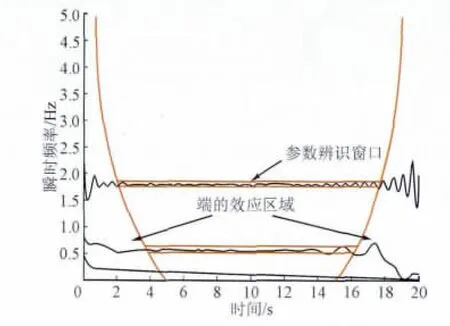
为了保证辨识的精度,对于IMF分量被端点效应污染的部分应该除去,主要依据分量的瞬时频率谱,以谱线较为平坦的部分作为辨识有效时窗,提高了辨识的精度。
2 技术研究与改进
HHT算法作为一种新生的信号分析方法,在理论上还有不成熟的地方,还有待于进一步研究与完善。下面对HHT算法应用中的问题做一些有益的分析和改进。
2.1 端点延拓
在EMD过程中的端点效应,尤其对于持续时长几秒钟至几分钟的低频振荡信号,是影响HHT方法辨识精度的主要因素。端点效应主要存在于EMD分解中的极值包络线端点延拓过程。以往主要应用直接延拓、对称延拓以及镜像延拓方法,一般分析长数列信号,且频率较高、筛分次数较少的情况下,端点效应可以影响到数据的两三个端头周期,不会对信号的分析结果有太大影响。但是对于低频振荡的短数据序列信号,尤其在非等幅振荡的情况下,端点效应的影响尤其显著,在筛分过程中的端点效应扩散将会导致分解结果失去物理意义。
本文提出了基于ARMA模型的端点预测算法。该算法通过建立AR模型,利用信号包络线本身的数据趋势预测极值点之外的包络线走向。
首先,建立AR预测模型,如公式(10)所示。
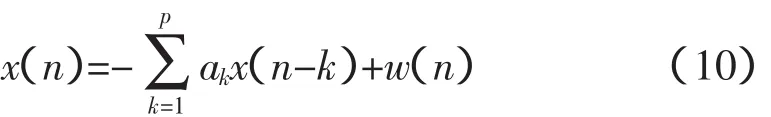
式中,x(n)代表测量数据;p是AR模型的阶数;ak代表模型参数;w(n)是均方差为σ2w的白噪声信号。利用自相关函数求解模型阶数p和参数ak。
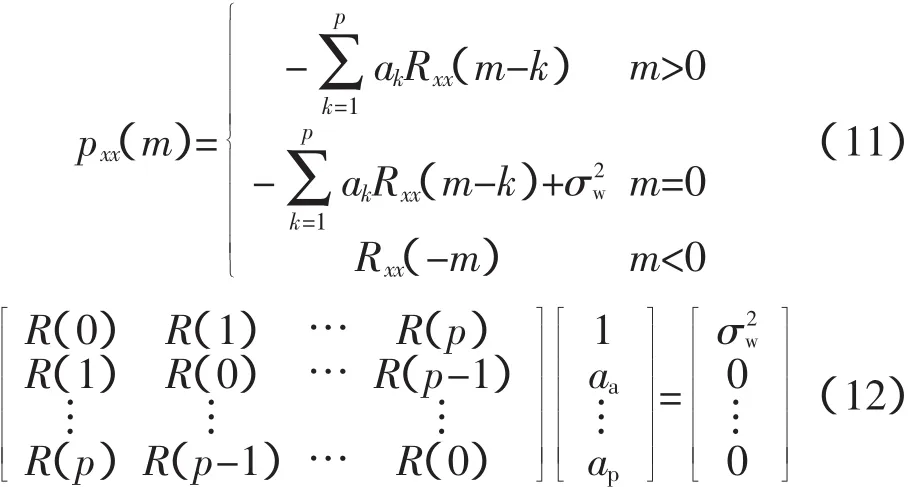
根据求解出AR模型参数,公式(10)可以预测x(n)的拓展序列。为验证AR延拓的有效性,本文对比了低频振荡信号包络线端点延拓的3种延拓方法,图1显示了比较结果。
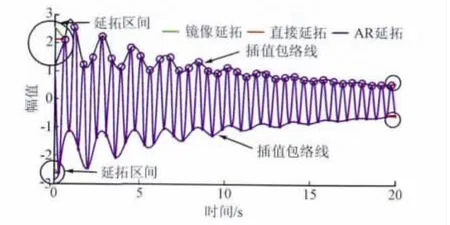
图1 端点延拓方法比较图Fig.1 Endpoint extension comparison chart
直接延拓缺点是不考虑信号内在特点,镜像延拓的缺点是对端点部分的阻尼振幅削弱过强,影响辨识精度。AR延拓可以有效减弱端点效应的影响,保留信号端头区域的阻尼特性。但是AR模型存在累积效应,预测准确度随着预测数据的增加显著下降,这可能引起附加误差。所以在该方法的应用中,本文设定了预测极限为20步,如果端点与时窗边界的距离超过该极限,采用镜像延拓方法替换,混合延拓方案在实际算法中具有更好的稳定性。
2.2 包络插值
传统EMD过程中的包络线插值采用三次样条插值方法,该插值算法的计算量较大,尤其对与低频振荡信号中的非均匀极值点,容易引起过冲和欠冲现象,可能产生一定范围内的频率漂移,对算法分析精度产生影响;同时三次样条插值方法加重了模态混叠和端点效应现象的影响,不利于低频振荡模态参数的提取。本文提出了基于B样条曲线的分段插值算法及混合插值算法,解决了三次样条插值算法容易引起的过冲和欠冲现象,同时也能有效地降低模态混叠程度。
B样条插值曲线不经过插值节点,是一种逼近曲线。首先,为了寻找出逼近真实包络线光滑曲线,先设计出控制多边形P0,P1,...,Pn和一个节点向量U={u0,u1,...,um},然后根据B样条递归算法求出所需光滑曲线。
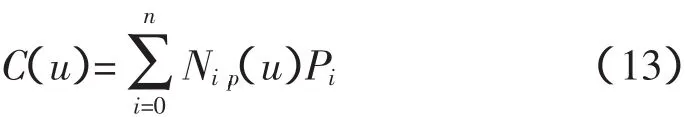
式中,Ni,p(u)是p次B-样条基函数;C(u)被称为节点,节点把B-样条曲线划分成曲线段,每个都定义在一个节点区间上。
本文应用分段幂函数插值算法的思想,容易构造一种基于B样条曲线的分段插值算法。如图2所示,先对型值点序列中的每三点用B样条曲线进行插值,再将这些分段B样条曲线按分段定理“拼接”起来,即得到基于B样条曲线的分段插值曲线,且该曲线是单值的。采用基于二次B样条曲线的分段插值算法对多个型值点插值,克服了采用三次样条插值法引起的过冲和欠冲问题。
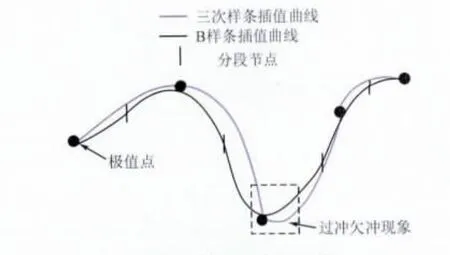
图2 插值算法对比图Fig.2 Interpolation algorithm comparison chart
2.3 筛分控制
IMF筛分过程去除了叠加波,这使得得到的IMF分量经Hilbert变换后得到的瞬时频率有意义。同时,筛分过程也使得振幅变化很大的相邻波形变得平滑,这有可能会去除有意义的振幅波动,得到振幅恒定,只有频率调制的IMF分量。
为了保证IMF分量的频率调制和幅度调制都有意义,必须确定IMF筛分过程的停止标准。目前的方法是通过计算连续2个筛分结果的标准差SD的值来定义,通常SD的值取在0.2与0.3之间[8]。对于电力系统振荡信号,从振动能量的角度分析,上述的停止筛分条件不能够有效解决过筛导致的阻尼幅度损失问题,即振动能量泄漏。
本文提出一种基于能量角度考虑的能量微差因子控制IMF分量的停筛条件。振动能量定义为:

通过计算连续2个筛分结果的能量微差:

得到能量微差因子,ε1是相邻2个IMF分量筛分过程中的残余能量差因子,ε2是残差信号和原始信号的能量差因子。应用在电力系统低频振荡信号EMD分解过程中,通过实验对比,定义能量差因子ε1取0.10~0.15来控制筛分的次数,使得到的IMF分量保留了原始数据中幅度调制的信息;定义ε2取值为0.1,结束EMD分解过程,通过该方法可以有效减少阻尼损失。
2.4 模态混叠
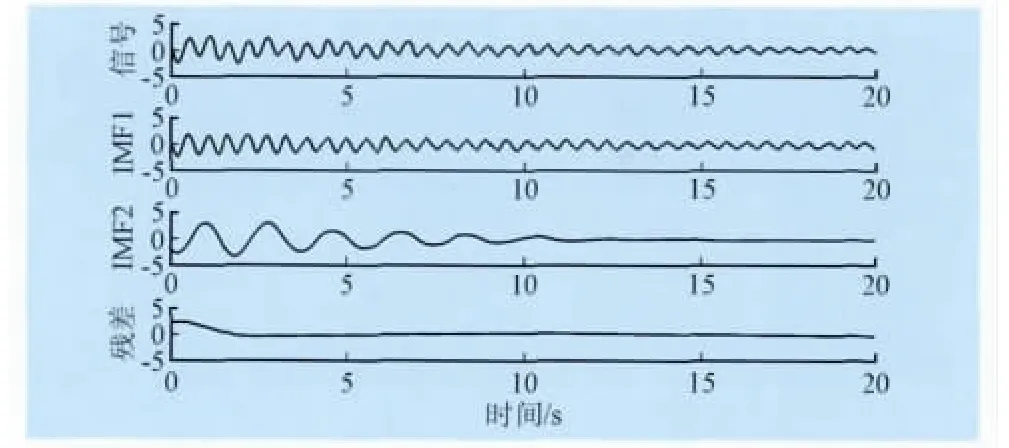
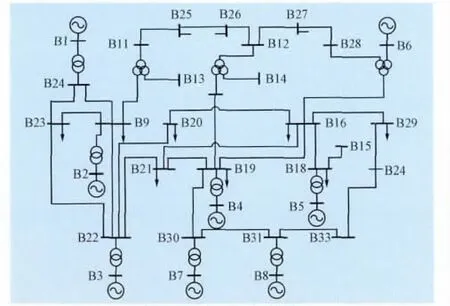
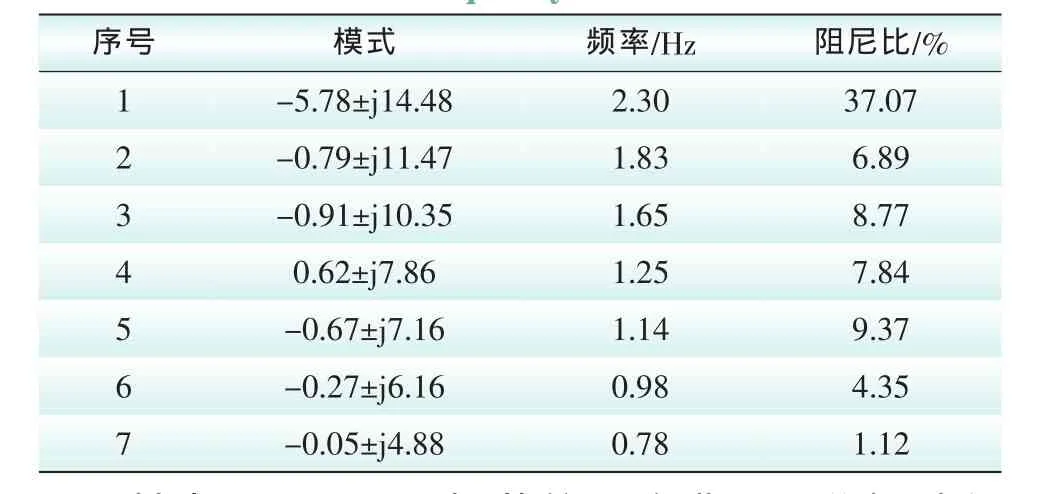
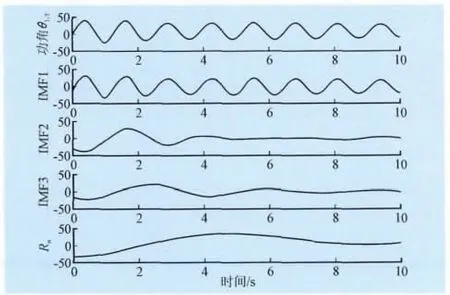
由于EMD算法本身的频率分辨局限性以及端点效应和插值误差的影响,当信号的时间尺度存在着跳跃性变化,或者2个模态频率比在区间0.5 本文中对于发生混叠的IMF信号利用小波方法再次分析振荡信号,影响该方法主要因素在于小波基的选择和频率分辨率。小波Mallat算法可以在没有明显损失的情况下,对信号进行多分辨分解,对信号具有局部分析和细化功能,还可以在时域内确定2种奇异点的位置。Mallat算法将多分辨小波分析简化成基本频率特性为ψ(ω)的带通滤波器在不同尺度a下对信号做滤波,并且这组滤波器具有品质因数恒定的特点。通过合理选择采样率和分解层数,就可以提取信号中感兴趣的低频振荡频率区间。利用小波分析对信号进行多尺度分析时,如果信号出现突变,其变换后系数具有模极大值,可以通过对模极大值点的检测来确定振荡发生的时刻,其幅值描述了振荡的发展趋势。 本文算法首先选择对信号具有紧支撑的小波基。选择与低频振荡信号特点相近似的Morlet小波作为母小波基,图3显示了Morlet小波在不同中心频率Fc=[1.0,0.5]Hz,以及带宽因子分别为Fb=[1.0,0.5]Hz状态下,小波函数波形和频谱分析结果,说明通过调节Morlet小波的参数可以在限定频带内检测出低频振荡特性信号。此外再根据振荡分量的频带特点和满足奇异点检测的结果选择分析窗口的长度,最后通过Mallat算法和Morlet小波参数的调节进行多分辨分析和时频域合成分析。 图3 Morlet小波中心频谱与带宽Fig.3 The center frequency and bandwidth of Morlet wavelet 针对多频信号经验模态分解中的模态混成现象,对于存在混叠IMF分量,结合小波分析方法,利用小波变换数据分析显微镜的特点,把混叠频带划分为限定带宽的窄带滤波器组,对出现混成模态IMF分量进行不同尺度下得Morlet小波分解,并根据小波分解后各频带信号的频率分布特征,选择能量比重较大的频带信号进行重构。将重构信号作为新的IMF分量,考察瞬时频谱的平坦性。本文的算法改进能有效提高EMD抗混叠分析能力,扩展算法的适用范围。 选择一个低频振荡测试信号,该信号由2个振荡模态组成,模态参数分别为s1=0.0652+j11.12,s1=0.1936+j3.3609。分析窗口20 s,采样率100 Hz,能量控制因子ε1=ε2=0.1,2个模态存在于分析窗口的整个时间域内,幅值分别为2和1,2个模态起始时刻相位差π/8。 图4显示了采用本文改进EMD方法筛分后的IMF分量结果。测试信号被分解为2个IMF分量和1个残差信号。从图形上看,IMF信号基本保持了携带的阻尼信息,能量泄露较小且没有收到模态混叠的影响。进一步通过Hilbert瞬时谱分析,结果显示在图5中。2个模态瞬时谱线的中部较为平坦,说明各IMF分量较为纯净,可认为单一振荡模态,通过辨识算法去除端点效应影响的数据列,同时利用3除粗差准则,得到较好的辨识数据窗口,根据最小二乘法计算振荡参数。 图4 两模态信号EMD分解图Fig.4 The two-mode signal EMD decomposition chart 图5 瞬时谱和参数辨识窗口Fig.5 The instantaneous spectral and parameter identification window 经过Hilbert谱分析和辨识计算,得到2个模态幅值分别为1.96和0.94,频率分别为1.73和0.51,衰减系数分别为-0.061和-0.188。辨识结果与测试信号特征基本符合,误差在5%以内。 考虑电科院EPRI-36仿真系统,拓扑图形在图6中描述。其中,潮流作业方式为全交流模式,电网BUS19处发生三相短路故障,故障消除时间在0.12 s。电网没有进行任何控制操作且电力系统的故障时间不超过稳定极限。 图6 EPRI-36拓扑图Fig.6 EPRI-36 topology diagram 低频振荡模式和频率及阻尼情况如表1所示。 表1 低频振荡模式Tab.1 Low frequency oscillations mode 其中BUS1~BUS7振荡信号改进EMD分解过程如图7描述,可以从图中看出各分解层次之间的能量泄露较小,基本上完整保留了每个振荡模态的能量信息,通过改进的参数识别算法获得一个有效成分(图中单个模态振荡的微分能量因子占总能量的90%以上,判定为主振模态),其他2个IMF分量携带能量很小,可认为是EMD分解端点效应和插值引起的能量泄漏,不对其进行模态辨识。 图7 功角振荡信号分解图Fig.7 Power angle oscillation signal decomposition diagram 通过本文推导的IMF分量与低频振荡模态参数辨识方法,得出IMF1的模态参数为:振荡频率0.77 Hz,振幅29.8,衰减系数-0.046,阻尼比0.93%。同时对比该段信号的Prony分析结果,除去拟合假频的影响,Prony分析的主振模态频率同样为0.77 Hz,阻尼比0.74%。通过结果对比能够说明,本文对HHT算法做的技术改进提高了算法的辨识精度,同时与理论结果对应性好,体现了改进技术在实际应用中具有较高的可行性和有效性,为该方法的工程应用提供了可靠的技术保障。 本文深入分析了影响HHT方法辨识低频振荡模式参数精度的技术问题,提出包括混合端点延拓、B样条插值、能量微差因子法和多分辨小波法等一系列技术改进方案,极大地抑制了传统算法中影响辨识精度的因素,实现了HHT方法整体性能的提升。通过仿真算例的测试分析,验证了该方法对低频振荡模式参数辨识具备较好的可行性和较高的辨识精度。但是,由于HHT算法中存在的端点效应和模态混叠等问题不能完全被消除,所以,有必要研究更加有效的改进方法,使得该方法的应用更加成熟可靠。 [1] 余贻鑫,李鹏.大区域电网弱互联对互联系统阻尼和动态稳定性的影响[J].中国电机工程学报,2005,25(11):6-11.YU Yi-xin,LI Peng.The impact of weak interaction of bulk power grids to damping and dynamic stability of power systems[J].Proceedings of the CSEE,2005,25(11):6-11(in Chinese). [2] 白雪峰,倪以信.电力系统动态安全分析综述[J].电网技术,2004,28(16):14-20.BAI Xue-feng,NI Yi-xin.Survey on dynamic security assessment of power systems[J].Power System Technology.2004,28(16):14-20(in Chinese). [3] 樊爱军,雷宪章,刘红超,等.研究大规模互联电网区域间振荡的特征值分析方法方法[J].电网技术,2005,29(17):35-39.FAN Ai-jun,LEI Xian-zhang,LIU Hong-chao,et al.Eigenvalue analysis methods for inter-area oscillations in large-scale interconnected power systems[J].Power System Technology,2005,29(17):35-39(in Chinese). [4]薛禹胜,郝思鹏,刘俊勇.关于低频振荡分析方法的评述[J].电力系统自动化,2009,33(3):1-8.XUE Yu-sheng,HAO Si-peng,LIU Jun-yong.A review ofanalysismethodsforlow-frequency oscillations[J].Automation of Electric Power,2009,33(3):1-8 (in Chinese). [5]常勇,吴靖,王超.基于广域信号的区域间低频振荡监视[J].电网与清洁能源,2011,27(5):16-21.CHANG Yong,WU Jing,WANG Chao.Monitoring of interarea oscillation based on wide area measurement signal[J].Power System and Clean Energy,2011,27(5):16-21(in Chinese). [6] HUANG N E.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Roral Society A,1998,45:903-995. [7]HUANG N E,WU M,LONG S,et al.A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J].Proceedings of the Roral Society A,2003,459:2317-2345. [8] 李天云,高磊,赵妍.基于HHT的电力系统低频振荡分析[J].中国电机工程学报,2006,26(14):24-30.LI Tian-yun,GAO Lei,ZHAO Yan.Analysis of low frequency oscillations using HHT method[J].Proceedings of the CSEE,2006,26(14):24-30(in Chinese). [9] MESSINA A R,VITTAL V.Non-stationary analysis of inter-area oscillations via Hilbert spectralanalysis[J].IEEE Transactions on Power Systems,2006,21(3):1234-1241. [10]MESSINA A R,VITTAL V,RUIZ V,et al.Interpretation and visualization of wide-area PMU measurements using Hilbert analysis[J].IEEE Transactions on Power Systems,2006,21(4):1763-1771. [11]宋明零,周力行,邓勇,等.HHT与傅立叶变换在电网故障分析中的仿真比较研究[J].电瓷避雷器,2011(6):21-30.SONG Ming-ling,ZHOU Li-xing,DENG Yong,et al.Simulation research and comparison on HHT and fourier transformation in network fault[J].Insulators and Surge Arresters,2011(6):21-30(in Chinese) [12]RILLING G,FLANDIN P,GONCALVES P.On empirical mode decomposition and its algorithms[C]//IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing,London,2003:1-6. [13]RILLING G,FLANDIN P,GONCALVES P.Empirical mode decomposition as a filter bank[J].IEEE Signal Process Letter.,2004,11(2):112-114. [14]杨德昌,REHTANZ C,李勇,等.基于希尔伯特-黄改进算法的电力系统低频振荡分析[J].中国电机工程学报,2011,31(10):102-108.YANG De-chang,REHTANZ C,LI Yong,et al.Researching on low frequency oscillation in power system based on improved HHT algorithm[J].Proceedings of the CSEE.2011,31(10):102-108(in Chinese). [15]蔡国伟,杨德友,张俊丰.基于实测信号的电力系统低频振荡模态辨识[J].电网技术,2011,35(1):59-65.CAI Guo-wei,YANG De-you,ZHANG Jun-feng.Mode identification of power system low-frequency oscillation based on measured signal[J].Power System Technology.2011,35(1):59-65(in Chinese). [16]康忠健,田爱娜,冯艳艳.基于HHT配电网不对称接地故障测距新方法[J].电网与清洁能源,2012,28(11):1-6.KANG Zhong-jian,TIAN Ai-na,FENG Yan-yan.A new method of asymmetric ground fault location based on the Hilbert-Huang Transform in distribution network[J].Power System and Clean Energy,2012,28(11):1-6(in Chinese). [17]DEERING R,KAISER J F.The use of masking signal to improve empirical mode decomposition[C]//Proc IEEE Int.Conf.Acoustics,Speech Signal Processing(ICASSP ′05),Philadelphia,PA,USA 2005:485-488. [18]SENROY N,SURYANARAYANAN S.Two techniques to enhance empirical mode decomposition for power quality applications[C]//IEEE PES General Meeting,Tampa,USA,2007:1-6.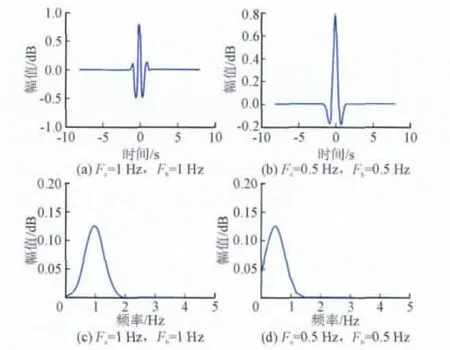
3 仿真分析
3.1 算例1
3.2 算例2
4 结论

