基于主导谐波频率的超高压输电线路单端故障测距算法

杨玉坤，杨永华，席皛，李伟，陈腾飞，郭玉天

（1.吉林省电力勘测设计院，吉林长春 130022；2.佛山市火力发电厂，广东佛山 528000；3.安阳供电公司，河南安阳 455000；4.新乡供电公司，河南新乡 453000）

输电线路的准确故障测距对于快速查找故障点，减轻故障巡线负担，减少停电检修时间，提高电网供电可靠性具有十分重要的意义[1]。

目前，超高压输电系统中的故障测距方法主要是行波法[2-5]。现有的行波故障测距原理仍存在一些问题[2-6]，如：识别波头的处理方法仍然不够完善；来自故障点和线路对端母线的反射波在一定条件下不能正确识别；当故障初相角过零时，测距精度较低；一些测距原理的测距精度还受到GPS和线路长度的影响等。

近年来，基于故障产生的暂态信号的保护原理——暂态量保护[7]得到了广泛的关注。这种新型的原理充分地提取和分析故障后的暂态信号，计算分析出其中含有的大量信息，如故障类型、方向、位置、持续时间等等，并具有速度快、不受过渡电阻、系统振荡和CT饱和等因素影响的特点。文献[8-10]分析了基于分布参数下的超高压输电线路故障暂态信号，提出了“主导谐波频率”的概念，并将其应用于超高压输电线路的继电保护、故障选相等领域。“主导谐波频率”的提取不需要很高的采样频率，充分利用其幅值、频率值、相位和衰减等特征能够构成各种新型的原理，并具有许多优良特性。本文将“主导谐波频率”应用于故障测距领域，并提出一种超高压输电线路单端故障测距算法。

本文利用运算法详细推导了分布参数下超高压输电线路各种故障类型时电流暂态信号的成分，得出了各种故障情形时故障位置与“主导谐波频率”的关系；并以“Prony算法”作为提取电流暂态特征量的工具；提出了一种基于“主导谐波频率”的超高压输电线路单端故障测距算法。ATP-EMTP仿真结果验证了本方案的有效性。

1 主导谐波频率

超高压输电线路一般采用分裂导线，分布电容较大，致使故障后的暂态过程十分明显，故障信号中包含大量衰减的高频分量[11]。各种暂态分量的存在使工频电流、电压的相位和波形发生了畸变，这对现有的基于工频量原理的装置产生了十分不利的影响。暂态量保护正是利用了这些衰减的暂态分量，从原理上克服了传统工频量保护的不足。

本文采用运算法分析超高压输电线路故障电流中高频暂态分量的特征，并应用叠加原理，仅对故障附加网络进行分析。

1.1 对称短路故障分析

如图1（a）所示系统（线路单位长度的正序参数已标注于图中），在F点发生了三相短路（距离M母线为l），对于M侧而言图1（b）为其短路附加网络。在短路附加网络中短路点所加电压源为短路前故障点的电压的负值。

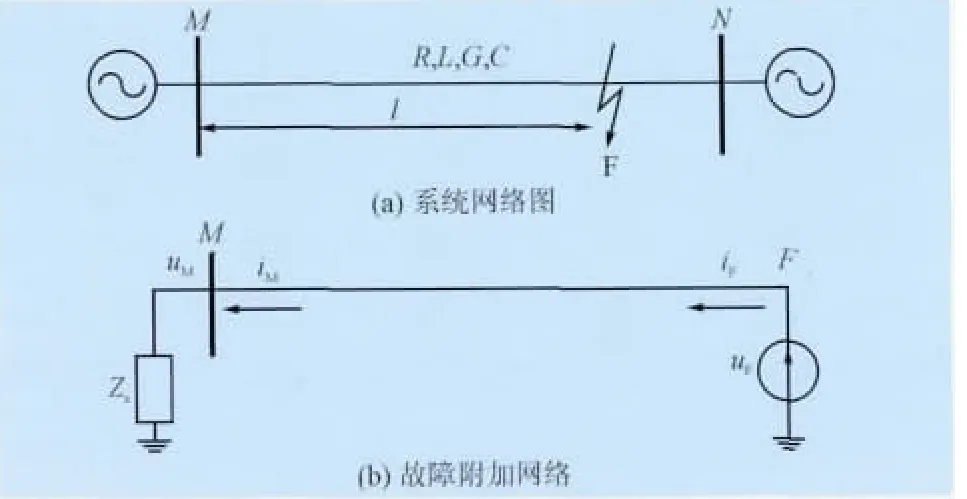
图1 系统网络图及故障附加网络Fig.1 System network and failure additional network

令M侧母线的电压和电流分别为uM（t）和iM（t），故障处的电压和电流分别为uF（t）和iF（t）。则由均匀传输线的长线方程可得它们之间的象函数的关系为：

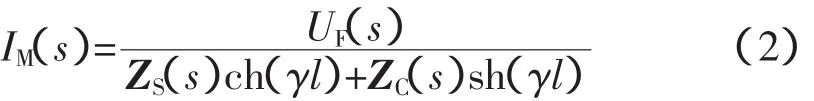
若短路附加网络中短路点所加电压源为uF（t）=-Emsin（ω0t+θ），则式可化为：

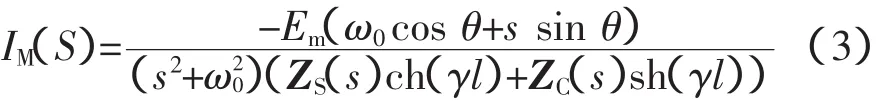
M侧电流的时域频率分量与式的极点具有对应关系，每一对共轭复根sn=-δn±jωn对应于一个角频率为ωn的频率分量。很明显，s=±jω0是一对共扼极点，它代表了iM（t）中的基波（工频）分量。iM（t）中的其他暂态分量由分母的另一个因式构成的超越函数的根决定：

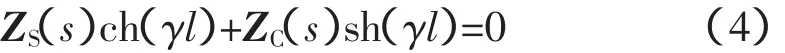
超越方程有无穷多个根，对应电流的时域具有无穷多个谐波形式的高频分量。

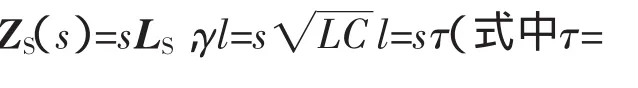
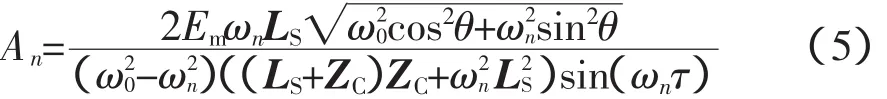
由于式（5）的分母中的阶数要高于分子中ωn的阶数，因此在某一特定的故障电流中，频率较大分量的幅值要小于频率较小分量的幅值。当θ=0°时，各幅值达到最小值，但不为零，即高频分量不会因为故障点电压过零而消失。据此构成的保护和测距原理将不受故障初相角过零的影响。

所有高频分量中频率最小的其幅值最大，最容易提取，能够代表故障特征，为故障暂态电流的“主导谐波频率”。综合上文的分析，对于某一特定的输电线路，故障电流中的“主导谐波频率”的频率值与系统内阻抗、线路特征阻抗、故障点位置有直接联系。

1.2 不对称短路故障分析

本文采用对称分量法来对不对称故障的故障附加网络进行分析。类似三相短路故障的分析方法，当区内F点发生不对称短路故障时，对于正序、负序和零序网络，每一序网均有如下M侧电流故障分量的表达式：

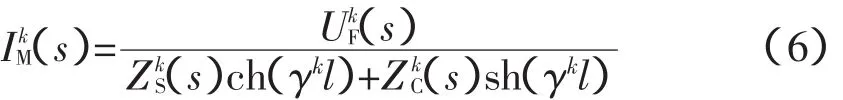
式中，上标k=1，2，0分别代表正序、负序和零序分量。将BC两相短路故障、A相接地故障、BC相接地故障的故障附加网络的边界条件变换到序网中，并联立式可得M侧相电流的故障分量分别为（设正、负序网的参数相等）：

由式（9）还可以进一步推得：

由式（7）和式（10）可知：两相短路的故障相电流表达式、两相接地的两故障相电流之差的表达式与三相短路时的式（2）具有相同的结构，那么它们的高频成分的特征与三相短路的相同，其频率最小的高频分量可作为此种故障类型的“主导谐波频率”。

对于单相接地故障，由式（8）可知各相电流的极点相同，但表达式非常复杂。这是由于零序网的参数和正、负序网的参数不同，从而产生了零模分量。由于零模分量的波速较小，比线模分量的频率低[12]，它将和线模分量共同反映在相电流中。但故障相中幅值最大的高频分量仍能够反映故障位置，可作为“主导谐波频率”。

2 故障测距算法

由上文的分析可以得出如下结论：各种故障类型时“主导谐波频率”能够反映故障位置，故障地点越远，“主导谐波频率”的频率值越小。

“主导谐波频率”频率值的求解即超越方程（4）的求解。由于“主导谐波频率”是频率值最小的分量，因此求解过程只考虑方程（4）的第一个根ω1。令方程第一个根为ω1，则可以得到ω1与故障点距离l的关系表达式：

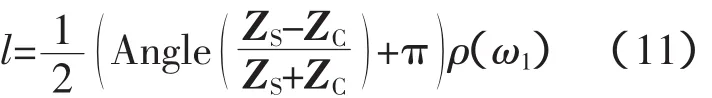
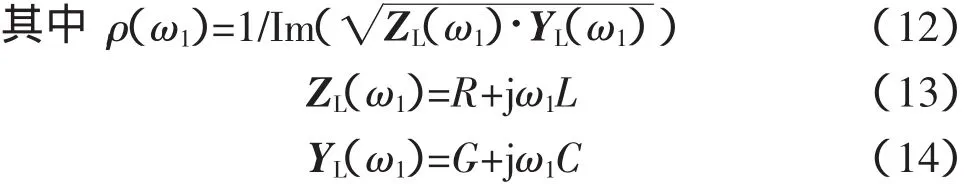
式中，Angle（）为求取复数的辐角，rad；ZS和ZC分别为角频率ω1下的系统内阻抗和线路特征阻抗；Im（）为求取复数的虚部。

因此，当“主导谐波频率”的值为f1时，ω1=2πf1，即可以由式（11）求得故障点的距离l。式（11）中R、L、G、C、ZC为已知的线路参数；而ZS包含随运行方式变化的系统内电阻和内电感，它们可由故障分量法在线计算[1]。

式（11）表明：故障地点越近，“主导谐波频率”的频率值越大。当故障地点很近时，“主导谐波频率”会大于二次设备数据采集系统的采样频率的一半；根据奎斯特采样定理，此时的"主导谐波频率"将无法提取出来。因此当“主导谐波频率”无法提取出时可认为线路出口故障，或者可以由线路另一侧的测距元件得出故障位置（此时另一侧的“主导谐波频率”的频率值很小）。图2是一典型500 kV输电线路不同故障位置时绘制的“主导谐波频率”的频率值随故障位置变化的关系曲线。

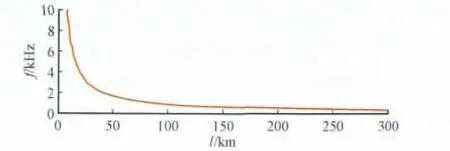
图2 “主导谐波频率”的频率值与故障位置的关系曲线Fig.2 Curve of the dominant harmonic frequencies and fault location

三相短路故障的“主导谐波频率”可以在任一相的暂态电流中提取。对于不对称短路故障，由本文第1.2节的“不对称短路故障分析”可知：①两相短路故障，“主导谐波频率”可以在任一故障相的暂态电流中提取；②两相接地故障，“主导谐波频率”可以在两故障相电流之差的暂态电流中提取；③单相接地故障，“主导谐波频率”可以在故障相的暂态电流中提取。

对于单相接地故障，由上文的分析可知：“主导谐波频率”将受到零模分量的影响，此时式（11）中的ρ（ω1）可以由式（15）计算，从而减少零模分量的影响程度。

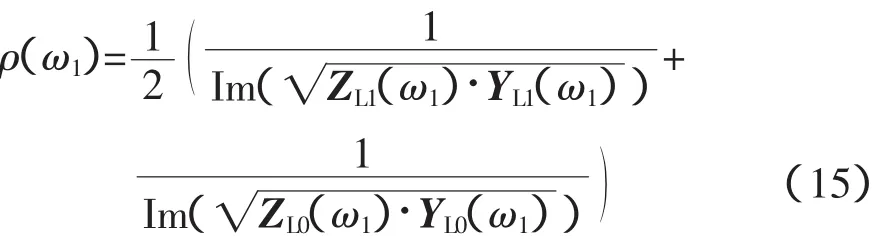
式中，ZL1（ω1）、YL1（ω1）和ZL0（ω1）、YL0（ω1）分别为线路正序和零序参数下的值。

因此，应用本文所提出的故障测距算法应先进行故障选相。故障选相可以由任何算法进行，也可以由基于“主导谐波频率”的故障选相方案[10]进行。当保护[9]、选相[10]、测距算法均使用基于“主导谐波频率”的方案，可以使二次设备的实时计算更加简洁。

3 主导谐波频率提取算法

超高压输电线路的故障位置与“主导谐波频率”具有直接的对应关系；各种故障类型时利用“主导谐波频率”实现故障测距的关键在于“主导谐波频率”的提取。

然而由于传统的信号处理方法（如基于傅里叶变换等算法）在处理衰减暂态信号上能力的不足，很难得到满意的结果。本文提出使用“Prony算法”来对故障衰减暂态信号进行“主导谐波频率”的提取。

Prony算法是于1795年为研究气体膨胀问题而提出的。它能够直接估算给定信号中包含的各周期分量及非周期分量的频率、幅值、衰减因子和初相[13]。近几年来该算法已在电力系统的低频振荡、动态系统辨识、继电保护、雷击干扰识别等研究领域取得了一定的成果[8-10，14-15]。

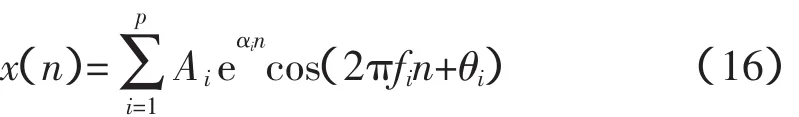
式（16）是Prony算法的求解模型，式中，p是模型的阶数；Ai、αi、fi、θi分别为第i个分量的幅值、衰减因子、频率和相位。当算法求解结果中某个分量的频率值为0时，说明此分量为非周期分量。

由于Prony算法在建模、求解过程中已经计及信号的衰减，并能够同时估算幅值和初相，因此它比传统的算法更加贴近实际的故障暂态信号，有足够的能力提取故障信号中的高频暂态成分，且基本不受信号中衰减周期、非周期分量的影响。

本文在Prony算法的求解过程中，使用“后向线性预测”技术[16]来对原始算法进行改进。改进之后的求解过程使信号中真实的频率成分所对应的极点和噪声所对应的极点分别划分于单位圆外和圆内，因此较好地解决了以往使用Prony算法时分析结果中由于噪声的干扰真实频率成分难于提取的难题。除此之外，对于算法中2个超定方程组的求解，本文使用“QR分解”技术，使方程组转化为非常容易求解的上三角方程组，大大缩短了Prony算法的计算耗时。改进之后的Prony算法保证了“主导谐波频率”提取的快速性和准确性。图3是一典型500 kV输电线路某位置三相短路故障时的故障暂态电流；图4是其B相经改进之后的Prony算法求解的结果（频率-幅值图）。

图3 典型500 kV输电线路故障暂态电流Fig.3 Typical fault transient current of the 500 kV transmission line

图4 Prony算法的求解结果Fig.4 Solution results of Prony algorithm

4 仿真分析

本文采用ATP-EMTP仿真软件对如图1（a）所示典型500 kV输电线路进行仿真，分析M侧测距元件在本文所提出算法下的计算结果。线路长度为200 km，其参数如下：R0=0.195 Ω/km，R1=0.027 Ω/km，L0=2.2121 mH/km，L1=0.8863 mH/km，C0=0.009 μF/km，C1=0.0127 μF/km。采样频率16 kHz。表1列出了不同故障位置、各种故障类型时的仿真分析结果。表2列出了当100 km处经不同过渡电阻发生三相短路时的仿真分析结果。

由上述仿真分析的结果可知，本文所提出的故障测距算法具有较好的准确度，仿真数据验证了本文理论部分的结论。由表1中的仿真计算数据可知：故障位置越远，“主导谐波频率”的频率值越小，验证了图2的结论。三相短路故障、两相短路故障、两相接地故障的仿真计算数据相近，是因为对于某一确定的故障位置，这3种故障类型的“主导谐波频率”是一致的，验证了本文第1.2节“不对称短路故障分析”的结论。对于单相接地故障，由于零模分量的影响，其误差较其他3种故障类型的略大，本文计算时已采用式（15）以减小误差。表2表明故障测距算法基本不受过渡电阻的影响

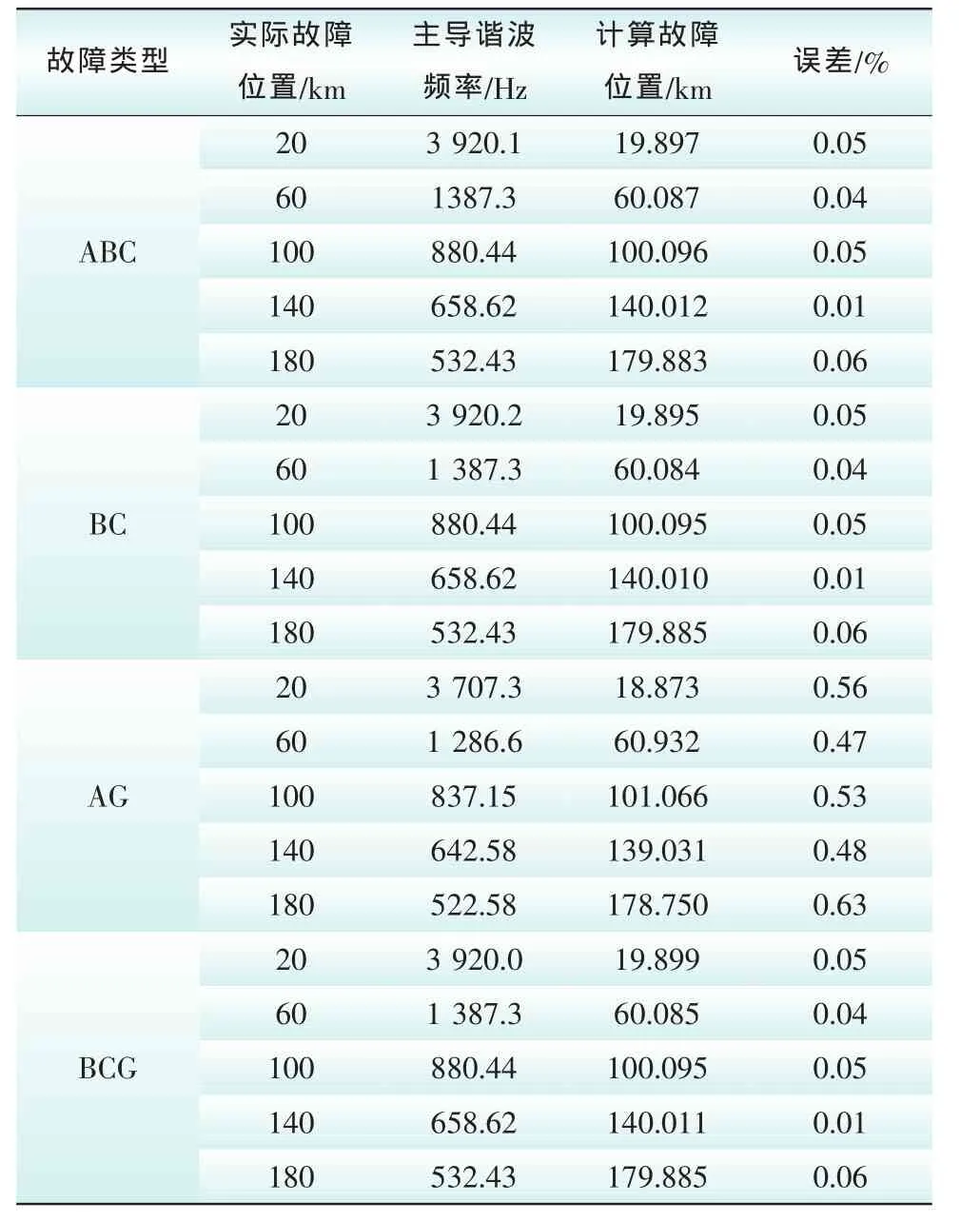
表1 不同故障位置、各种故障类型时的仿真分析结果Tab.1 Analytic results of different fault types for fault at different locations

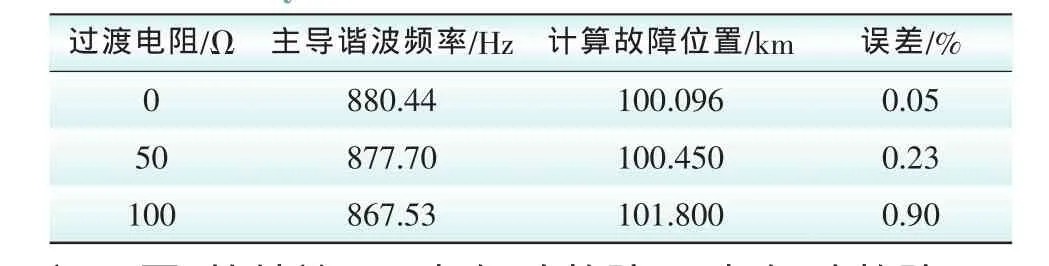
表2 不同过渡电阻时的仿真分析结果Tab.2 Analysis results of different transition resistances

5 结论

1）各种故障类型时的故障暂态电流中包含谐波形式的高频分量。“主导谐波频率”的频率值与系统内阻抗、线路特征阻抗、故障点位置有直接联系。本文给出了故障点的距离与“主导谐波频率”的频率值之间的表达式，并据此提出了一种单端故障测距算法，该算法具有不受故障初相角过零的影响等优点。

2）Prony算法更加贴近实际的故障模型，能够很好地提取故障信号中的高频暂态分量的特征。本文使用后向线性预测和QR分解技术，使算法的分析结果更加准确、可靠、快速。

3）故障测距算法的性能经受了大量ATP-EMTP仿真数据的测试，在不同故障位置、不同故障类型、不同过渡电阻等故障条件下都具有较好的准确度。

[1] 葛耀中．新型继电保护与故障测距原理与技术[M]．西安：西安交通大学出版社，1996.

[2] 刘万超，李玮，孙佳佳，等.基于多分辨形态梯度-相关函数综合测距算法的单端行波故障测距[J].电网技术，2011（10）:225-229.LIU Wan-chao， LI Wei， SUN Jia-jia， et al.Single terminal traveling wave fault location based on fault location algorithm integrating multi-resolution morphological gradient with correlation function[J].Power System Technology，2011（10）:225-229（in Chinese）.

[3] 郑州，吕艳萍，王杰，等.基于小波变换的双端行波测距新方法[J].电网技术，2010（1）:203-207.ZHENG Zhou，L譈 Yan-ping，WANG Jie，et al.A new two-terminal traveling wave fault location method based on wavelet transform[J].Power System Technology，2010（1）:203-207（in Chinese）.

[4] 刘万超，陈平，马永明，等.基于多时窗相关函数和形态学滤波的单端行波故障测距研究[J].电力系统保护与控制，2009（20）:28-33.LIU Wan-chao，CHEN Ping，MA Yong-ming，et al.Study of fault locating based on single terminal traveling waves using multi-window correlation functions and mathematical morphological filtering algorithm[J].Power System Protection and Control， 2009（20）:28-33 （in Chinese）.

[5] 束洪春，邬乾晋，张广斌，等.基于神经网络的单端行波故障测距方法[J].中国电机工程学报，2011（4）:85-92.SHU Hong-chun，WU Qian-jin，ZHANG Guang-bin，et al.Single terminal traveling wave fault location method based on ANN[J].Proceedings of the CSEE，2011（4）:85-92（in Chinese）.

[6] 李一峰，陈平.利用故障线路暂态波形的新型故障测距方法[J].继电器，2009，36（6）:4-7，31.LI Yi-feng，CHEN Ping.Method in fault location using fault tripping induced travelling waves[J].Relay，2009，36（6）:4-7，31（in Chinese）.

[7] 薄志谦.新一代电力系统继电保护：暂态保护[J].电网技术，1996，20（3）:34-36.BO Zhi-qian.Transient based protection：A new generation of power system protection[J].Power System Technology，1996，20（3）:34-36（in Chinese）.

[8] 杨玉坤.基于Prony算法的超高压输电线路暂态量保护的研究[D].保定:华北电力大学，2011.

[9] 杨明玉，杨玉坤.基于后向预测Prony算法的超高压输电线路暂态量保护方案[J].电力自动化设备，2011，31（5）:28-33.YANG Ming-yu，YANG Yu-kun.EHV power transmission line transient-based protection with backward Prony algorithm[J].Electric Power Automation Equipment，2011，31（5）:28-33（in Chinese）.

[10]杨明玉，杨玉坤.基于后向预测Prony算法的超高压输电线路故障选相方案[J].电力系统保护与控制，2011（19）:94-99.YANG Ming-yu，YANG Yu-kun.EHV transmission line faulty phase selection scheme based on backward prony algorithm[J].Power System Protection and Control，2011（19）:94-99（in Chinese）.

[11]朱声石.高压电网继电保护原理与技术[M].北京:中国电力出版社，2005:59-82.

[12]SWIFT G W.The spectra of fault-induced transients[J].IEEE Transactions on Power Apparatus and Systems，1979，PAS-98（3）:940-947.

[13]张贤达.现代信号处理[M].北京:清华大学出版社，2002:119-125.

[14]郭成，李群湛，王德林.互联电力系统低频振荡的广域Prony分析[J].电力自动化设备，2009，29（5）:69-73.GUO Cheng，LI Qun-zhan，WANG De-lin.Wide-area Prony analysis of low frequency oscillation in interconnected power system[J].Electric Power Automation Equipment，2009，29（5）:69-73（in Chinese）.

[15]杨玉坤，陈曦，田浩.基于Prony算法的输电线路雷击干扰识别研究[J].陕西电力，2010，38（10）:14-18.YANG Yu-kun，CHEN Xi，TIAN Hao.Application of prony algorithm in lightning interference detection of transmission line[J].Shaanxi Electric Power，2010，38（10）:14-18（in Chinese）.

[16]KUMARESAN R，TUFTS D.Estimating the parameters of exponentially damped sinusoids and pole-zero modeling in noise[J].IEEE Transactions on Acoustics，Speech and Signal Processing，1982，30（6）:833-840.